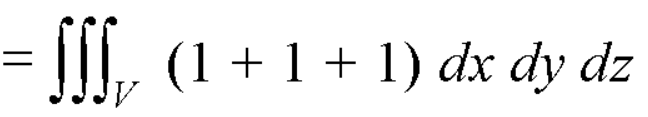Unit – 4
Multivariable calculus: Integration
Q1) Evaluate 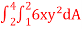 , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
A1) Let, I = 
= 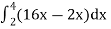
= 
= 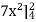
= 84 sq. unit.
which is the required area.
Q2) Evaluate the following double integral,
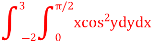
A2) Let,
I = 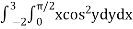
On solving the integral, we get
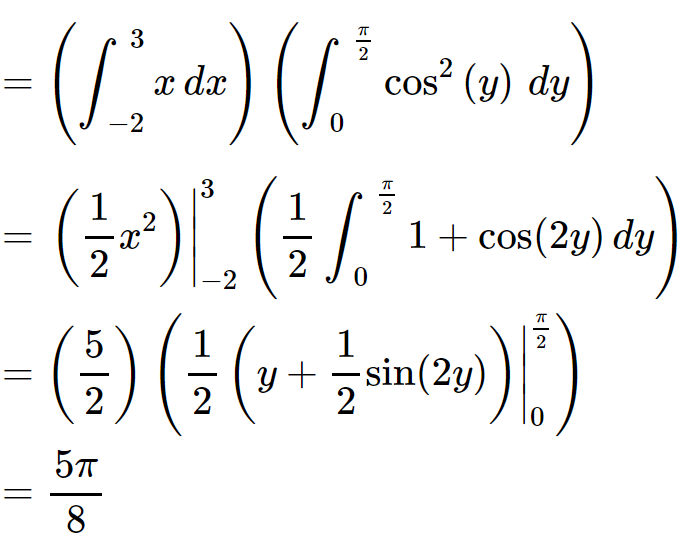
Q3) Evaluate 
A3) Let the integral,
I = 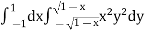
=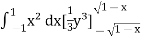
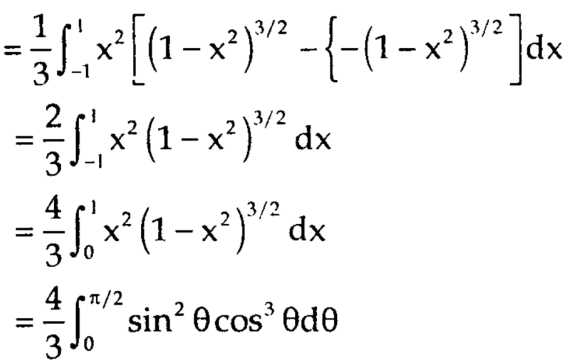
Put x = sinθ
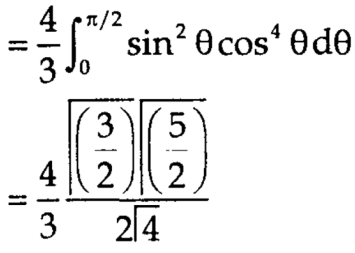
= π / 24 ans.
Q4) Evaluate
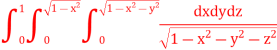
A4) Let
I = 
= 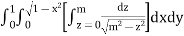
(Assuming m = 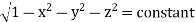 )
)
= 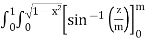 dxdy
dxdy
= 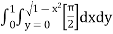
=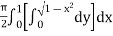
= 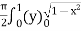 dx
dx
=  dx
dx
= 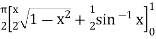
=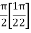
I =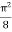
Q5) Find Volume of the tetrahedron bounded by the co-ordinate’s planes and the plane
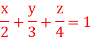
A5) Volume =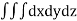 ………. (1)
………. (1)
Put 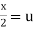 ,
, 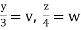

From equation (1) we have
V = 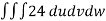
=24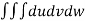
=24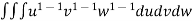 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 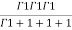
= =
=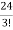 = 4
= 4
Volume =4
Q6)
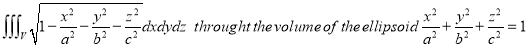
A6) - Put

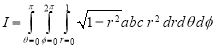
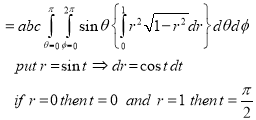
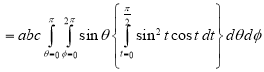
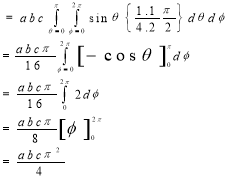
Q7) Express as single integral and evaluate dy dx + dy dx.
A7)
Given: I = dy dx + dy dx
I = I1 + I2
The limits of region of integration I1 are
x = – ; x = and y = 0, y = 1 and I2 are x = – 1,
x = 1 and y = 1, y = 3.
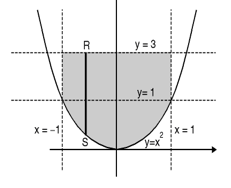
The region of integration is as shown in Fig.
To consider the complete region take a vertical strip SR along the strip y varies from y = x2 to
y = 3 and x varies from x = –1 to x = 1. Fig.
I = 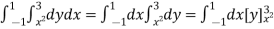
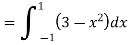
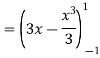
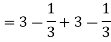

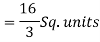
Q8) Evaluate-
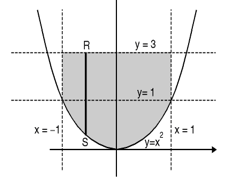
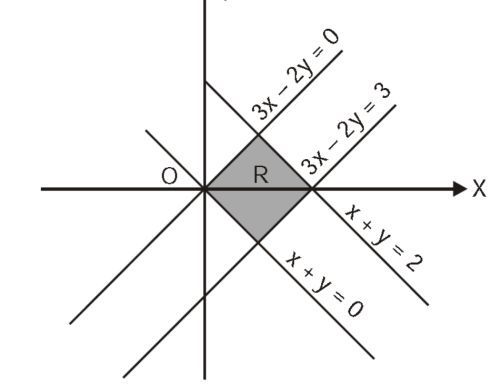
Where- R is the region bounded by a parallelogram- x + y = 0, x + y = 2, 3x – 2y = 0, 3x – 2y = 3.
A8)
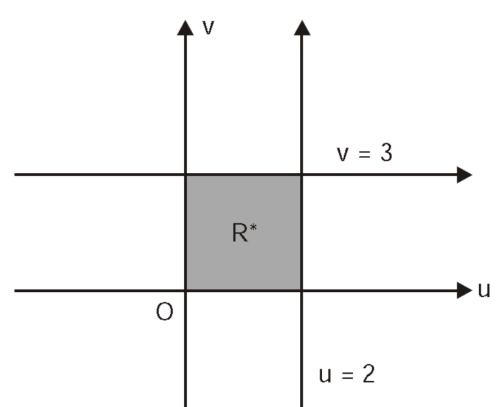
By changing the variables x, y to the new variables u and v, by the substitution x + y = u, 3x – 2y = v, the given parallelogram R reduces to a rectangle 
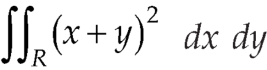
The required Jacobian is-

Since u = x + y and u = x + y = 2, here u varies from 0 to 2 while v varies from 0 to 3.
Since-
3x – 2y = v = 0, 3x – 2y = v = 3
Therefore, the integral will be in new variables-
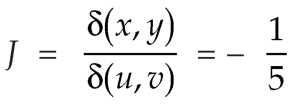
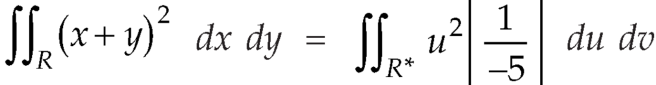

which is the required answer.
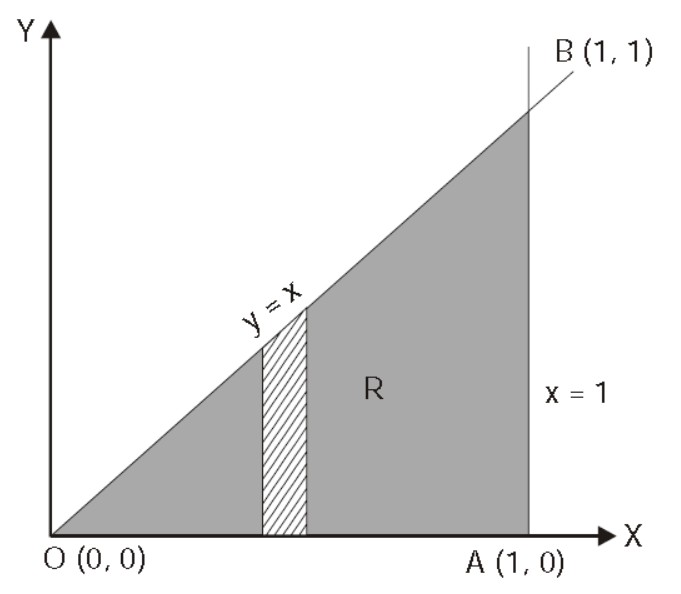
Q9) Evaluate 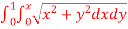 the transformation is x = v and y = uv.
the transformation is x = v and y = uv.
A9) Here the region of integration R is the triangle which is bounded by y = 0, x = 1 and y = x
Here put,
X = u and y = uv, we get-
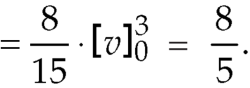
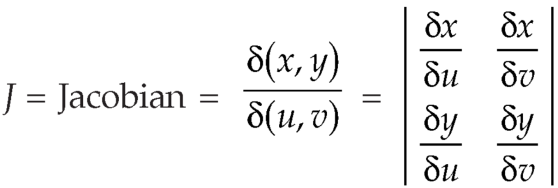
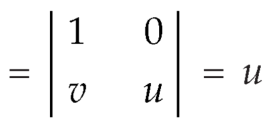
Here x varies from 0 to 1 while y varies from 0 to x.
Since u = x so u varies from 0 to 1
Here, similarly, since  , so that v varies from 0 to 1. Thus-
, so that v varies from 0 to 1. Thus-
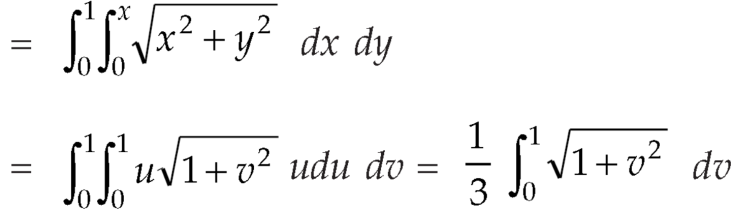
Q10) Find the area between the parabola y ² = 4ax and another parabola x² = 4ay.
A10) Let,
y² = 4ax ………………... (1)
and
x² = 4ay…………………. (2)
then if we solve these equations, we get the values of points where these two curves intersect
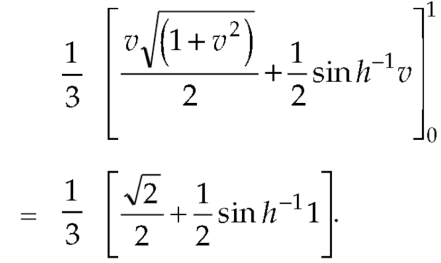
x varies from y²/4a to  and y varies from o to 4a,
and y varies from o to 4a,
Now using the concept of double integral,
Area = 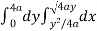

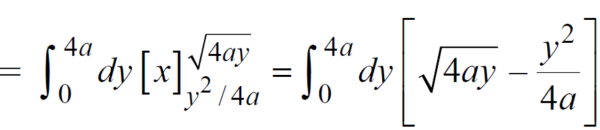
Q11) Apply Green’s theorem to evaluate 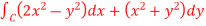 where C is the boundary of the area enclosed by the x-axis and the upper half of circle
where C is the boundary of the area enclosed by the x-axis and the upper half of circle 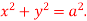
A11) We know that by Green’s theorem-
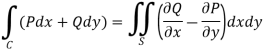
And it given that-

Now comparing the given integral-
P = 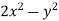 and Q =
and Q = 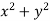
Now-
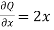 and
and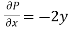
So that by Green’s theorem, we have the following integral-
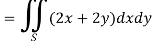
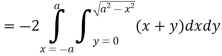
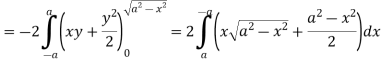
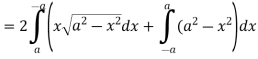
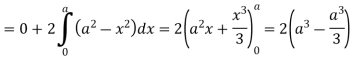
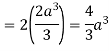
Q12) Verify green’s theorem in xy-plane for  where C is the boundary of the region enclosed by
where C is the boundary of the region enclosed by 
A12) On comparing with green’s theorem,
We get-
P = 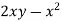 and Q =
and Q = 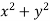
 and
and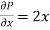
By using Green’s theorem-
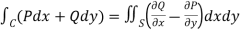 ………….. (1)
………….. (1)
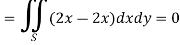
And left-hand side= 
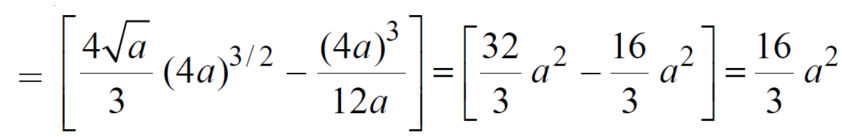 ………….. (2)
………….. (2)
Now,
Along 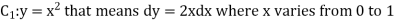
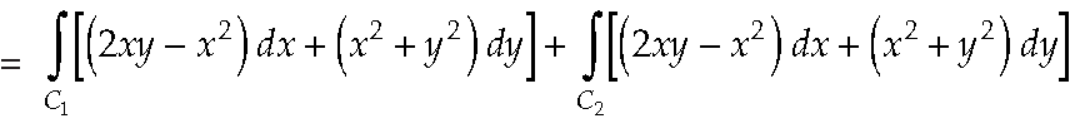
Along 

Put these values in (2), we get-
L.H.S. = 1 – 1 = 0
So that the Green’s theorem is verified.
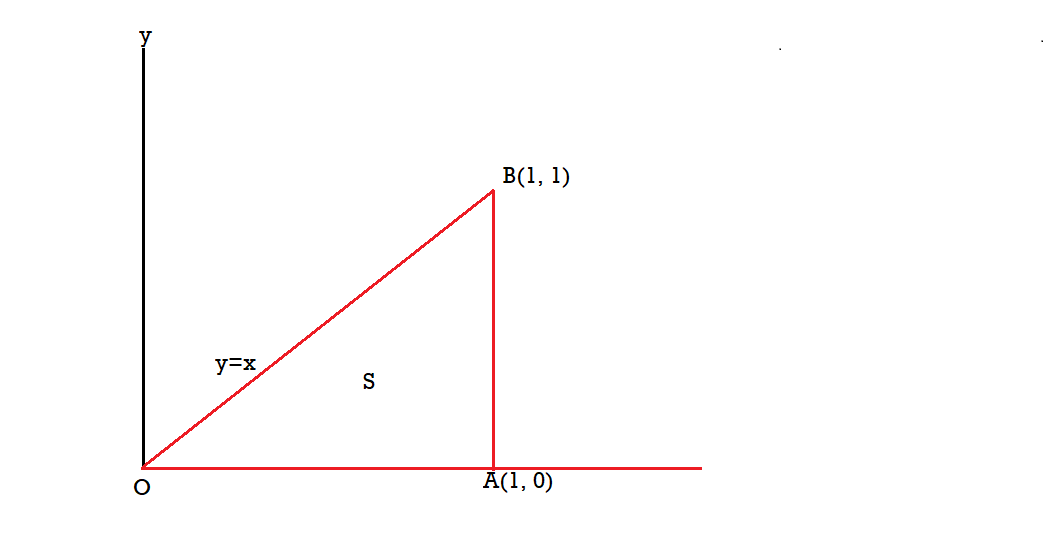
Q13) If  and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate
and C is the boundary of the triangle with vertices at (0, 0, 0), (1, 0, 0) and (1, 1, 0), then evaluate 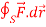 by using Stoke’s theorem.
by using Stoke’s theorem.
A13) Here we see that z-coordinates of each vertex of the triangle is zero, so that the triangle lies in the xy-plane and 
Now,
Curl 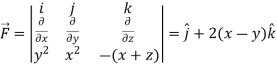
Curl 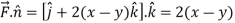
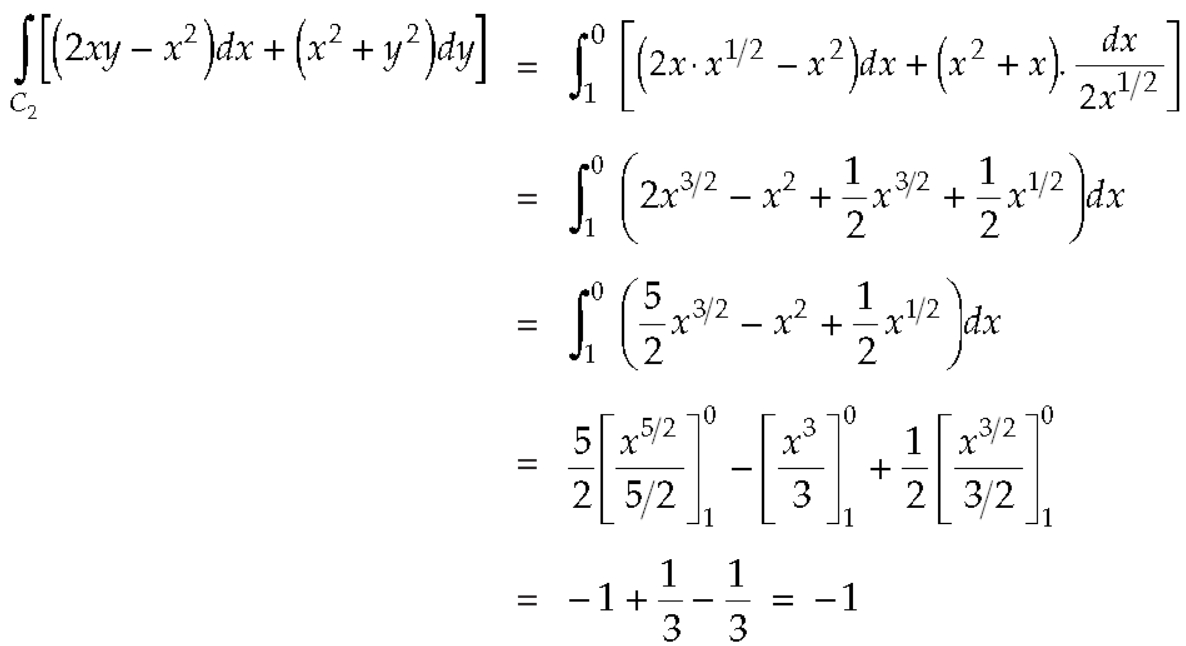
The equation of the line OB is y = x
Now by stoke’s theorem,
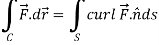
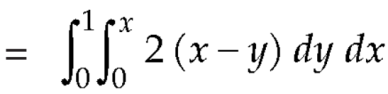
Q14) Show that 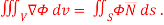
A14) By divergence theorem, 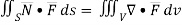 ...… (1)
...… (1)
Comparing this with the given problem let
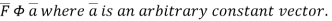
Hence, by (1)
 …………. (2)
…………. (2)
Now,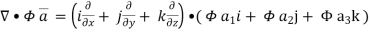
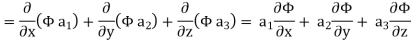
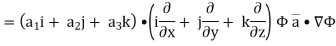
Hence, from (2), We get,
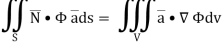
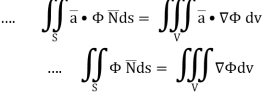
Q15) By using divergence theorem to evaluate-
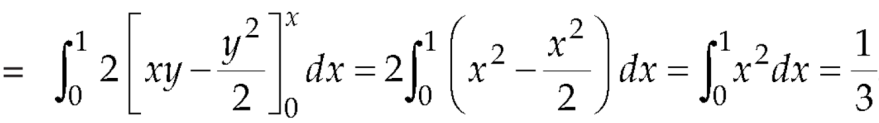
Where-

And S is the surface of the sphere 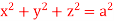 .
.
A15)

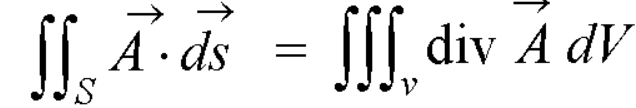
On putting x = 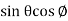 , y =
, y = 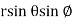 , z =
, z = 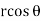 , we get-
, we get-
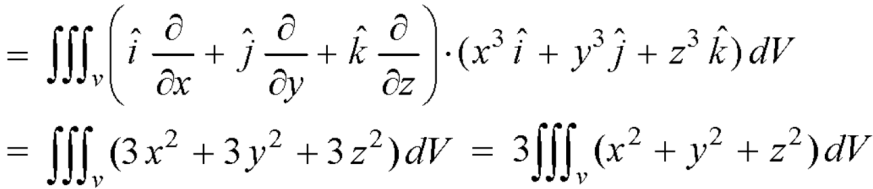
Q16) Use the divergence theorem to evaluate-
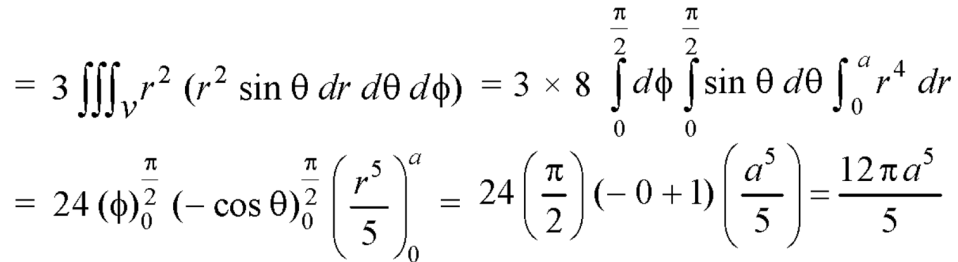
Over the surface of a sphere of radius ‘a’.
A16)
Here we have-
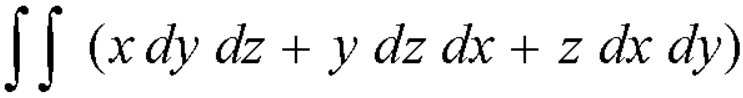
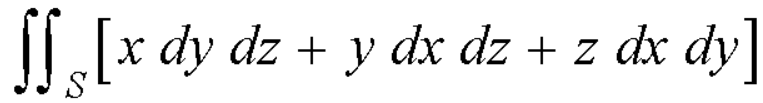
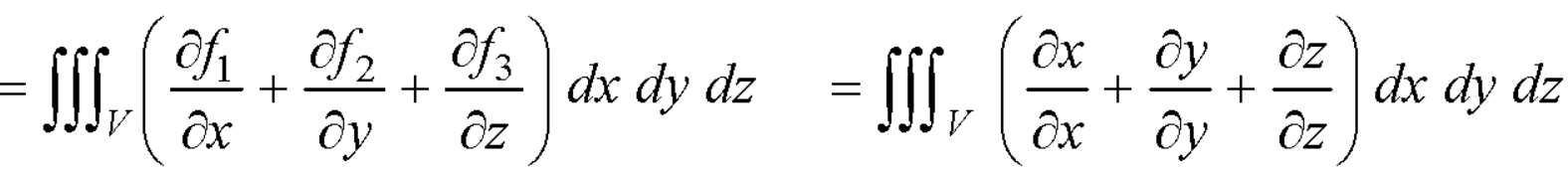
= 3 × Volume of the sphere