Unit – 7

Partial differential equations

Q1) Solve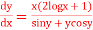

A1)

We have,

Separating the variables, we get

(sin y + y cos y) dy = {x (2 log x +1} dx

Integrating both the sides we get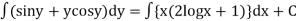

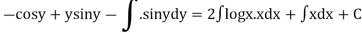
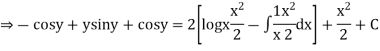
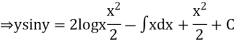
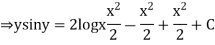
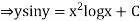
Q2) Solve the differential equation

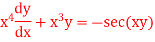
A2)

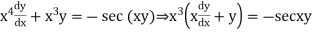
Put,

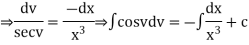
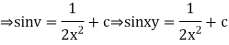
Q3) Solve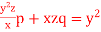

A3) Rewriting the given equation as

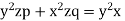
The subsidiary equations are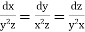

The first two fractions give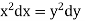

Integrating we get 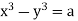   n (i)

Again, the first and third fraction give xdx = zdz

Integrating, we get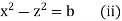

Hence from (i) and (ii), the complete solution is

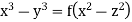
Q4) Solve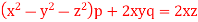

A4)

Here the subsidiary equations are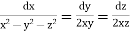

From the last two fractions, we have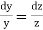

Which on integration gives log y = log z + log a or y/z=a   (i)

Using multipliers x, y and z we have

Each fraction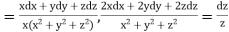

Which on integration gives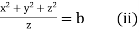

Hence from (i) and (ii) the required solution is

Q5) Solve-

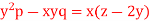
A5)

We have-

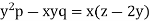
Then the auxiliary equations are-

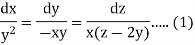
Consider first two equations only-

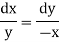
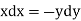
On integrating

…….. (2)

Now consider last two equations-

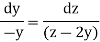
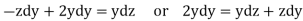
On integrating we get-

…………… (3)

From equation (2) and (3)-

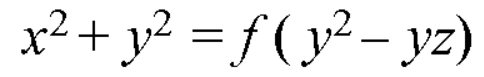
Q6) Find the general solution of-

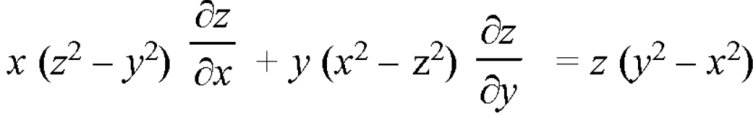
A6)

The auxiliary simultaneous equations are-

……….. (1)

Using multipliers x, y, z we get-

Each term of (1) is equals to-

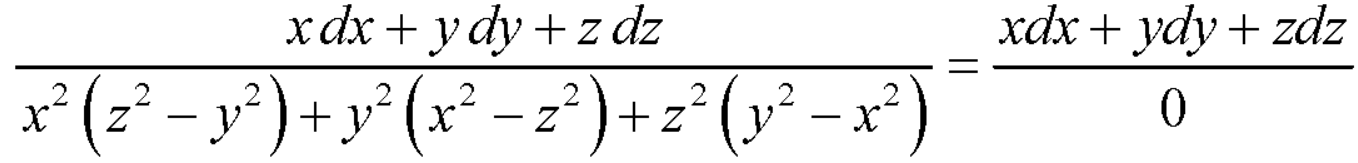
Xdx + ydy + zdz=0

On integrating-

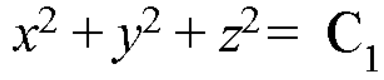………… (2)

Again equation (1) can be written as-

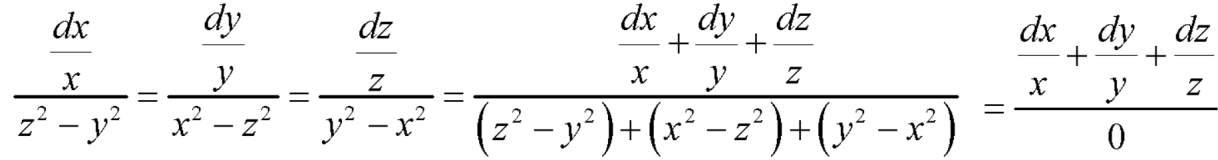
Or

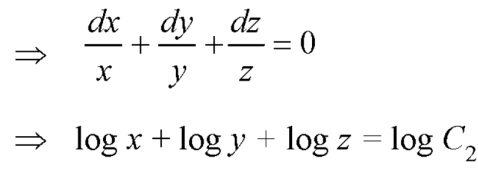
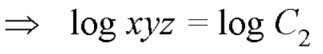
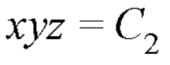………….. (3)

From (2) and (3), the general solution is-

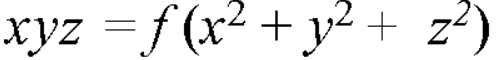
Q7) Solve-

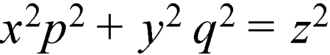
A7)

This equation can be transformed as-

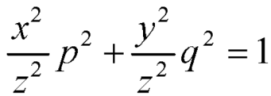
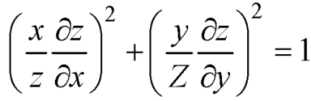
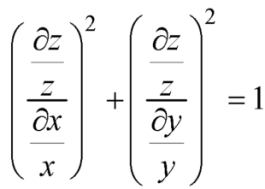………. (1)

Let

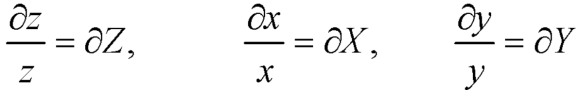
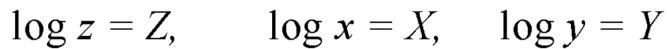
Equation (1) can be written as-

………… (2)

Let the required solution be-

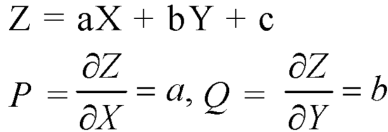
From (2) we have-

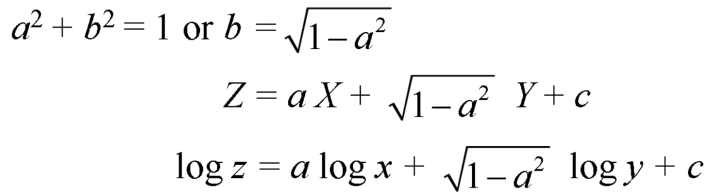
Q8) Solve-

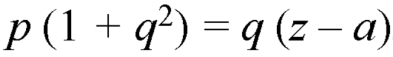
A8)

Let u = x + by

So that-

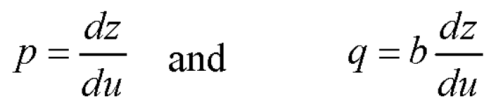
Put these values of p and q in the given equation, we get-

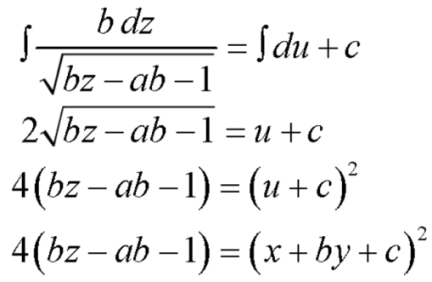
Q9) Solve-

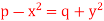
A9)

Let-

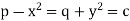
That means-

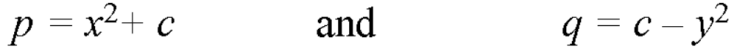
Put these values of p and q in