|
|
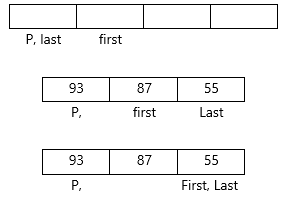
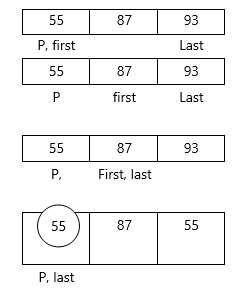
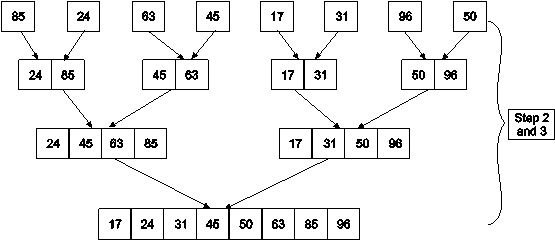
C function for Quick sort
x=0,y=n–1
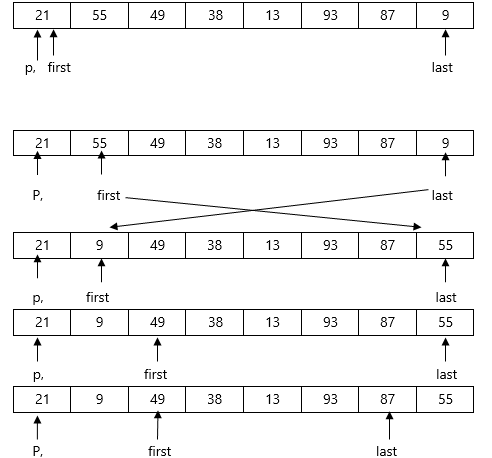
void Quicksort(A,x,y)
{
if(x<y)
{
first=x;
last=y;
p=A[x];
while(first<last)
{
while(A[first]<p)
first++;
while(A[last]>p)
last ––;
if(first<last)
swap(A[first],A[last])
}
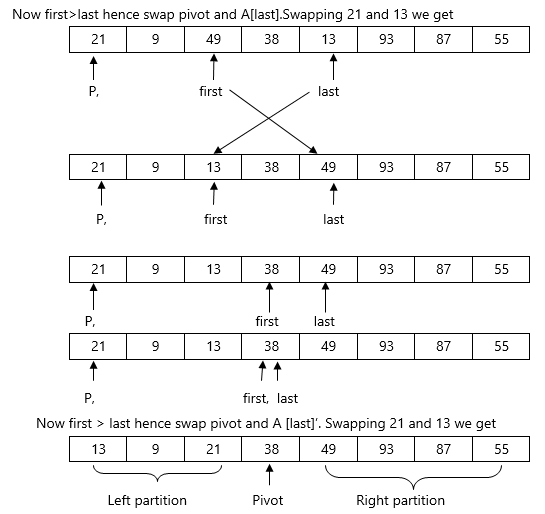
swap(A[x],A[y])
Quicksort(A,x,last–1);
Quicksort(A,first+1,y);
}
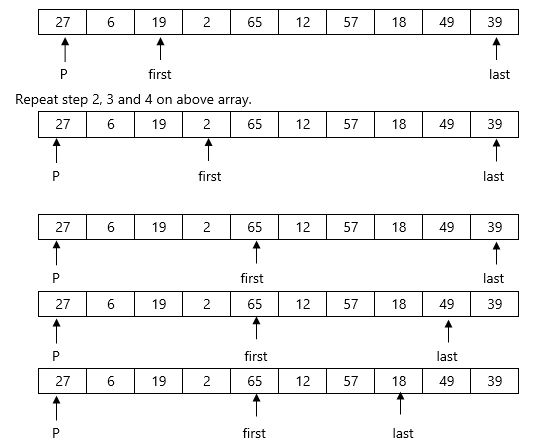
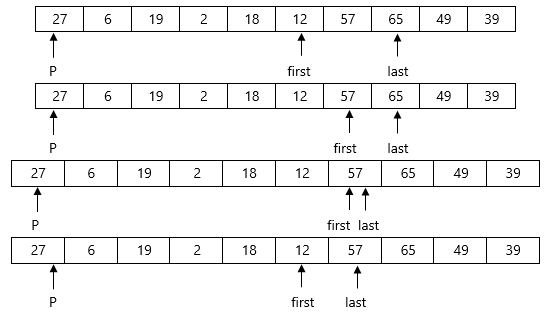
We will see examples on Quick sortExample : Apply Quicksort on array A= {27,6,39,2,65,12,57,18,49,19}
|
|
|
12 | 6 | 19 | 2 | 18 | 27 | 57 | 65 | 49 | 39 |
12 | 6 | 19 | 2 | 18 | 27 | 57 | 65 | 49 | 39 |
2 | 6 | 12 | 19 | 18 | 27 | 57 | 65 | 49 | 39 |
2 | 6 | 12 | 18 | 19 | 27 | 57 | 65 | 49 | 39 |
2 | 6 | 12 | 18 | 19 | 27 | 49 | 39 | 57 | 65 |
2 | 6 | 12 | 18 | 19 | 27 | 39 | 49 | 57 | 65 |
2 | 6 | 12 | 18 | 19 | 27 | 39 | 49 | 57 | 65 |
|
|
|
|
|
|
|
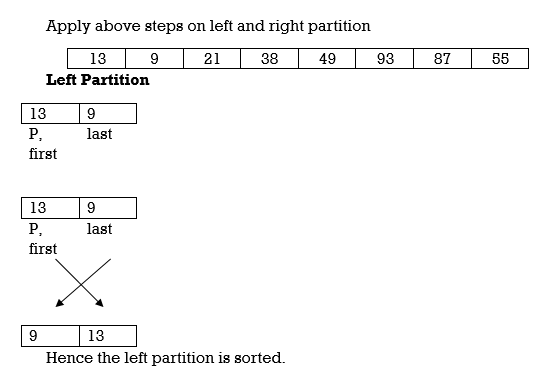
9 | 13 | 21 | 38 | 49 | 55 | 87 | 93 |
|
24 | 85 |
| 45 | 63 |
| 17 | 31 |
| 50 | 96 |
24 | 85 | 63 | 85 |
| 17 | 31 | 50 | 96 |
17 | 24 | 31 | 45 | 50 | 63 | 85 | 96 |
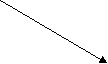 LB >y, then the remaining elements of A are assigned to C. Thus the algorithm becomes MERGING ( A, x, B, y, C) 1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1 2. [Compare] Repeat while LA <= x and LB <= y If A[LA] < B[LB] , then (a) [Assign element from A to C ] set C[LC] = A[LA] (b) [Update pointers ] Set LC := LC +1 and LA = LA+1 Else (a) [Assign element from B to C] Set C[LC] = B[LB] (b) [Update Pointers] Set LC := LC +1 and LB = LB +1 [End of loop] 3. [Assign remaining elements to C] If LA >x , then Repeat for K= 0 ,1,2,........,y–LB Set C[LC+K] = B[LB+K] [End of loop] Else Repeat for K = 0,1,2,......,x–LA Set C[LC+K] = A[LA+K] [End of loop] 4. Exit
LB >y, then the remaining elements of A are assigned to C. Thus the algorithm becomes MERGING ( A, x, B, y, C) 1. [Initialize ] Set LA : = 1 , LB := 1 AND LC : = 1 2. [Compare] Repeat while LA <= x and LB <= y If A[LA] < B[LB] , then (a) [Assign element from A to C ] set C[LC] = A[LA] (b) [Update pointers ] Set LC := LC +1 and LA = LA+1 Else (a) [Assign element from B to C] Set C[LC] = B[LB] (b) [Update Pointers] Set LC := LC +1 and LB = LB +1 [End of loop] 3. [Assign remaining elements to C] If LA >x , then Repeat for K= 0 ,1,2,........,y–LB Set C[LC+K] = B[LB+K] [End of loop] Else Repeat for K = 0,1,2,......,x–LA Set C[LC+K] = A[LA+K] [End of loop] 4. Exit Program for Merge Sort
#include<stdio.h>
#define MAX 50
void mergeSort(int A[],int first,intmid,int high);
void divide(int A[],int first,int last);
int main(){
int merge[MAX],i,n;
printf("Enter the total number of elements: ");
scanf("%d",&n);
printf("Enter the elements which to be sort: ");
for(i=0;i<n;i++){
scanf("%d",&merge[i]);
}
divide(merge,0,n–1);
printf("After merge sorting elements are: ");
for(i=0;i<n;i++){
printf("%d ",merge[i]);
}
return 0;
}
void divide(int A[],int first, int last)
{
int mid;
if(first<last){
mid=(first+last)/2;
divide(A,first,mid);
divide(A,mid+1,last);
mergeSort(A,first,mid,last);
}
}
void mergeSort(int A[],int first,intmid,int last)
{
int i,m,k,l,temp[MAX];
l=first;
i=first;
m=mid+1;
while((l<=mid)&&(m<=last)){
if(A[l]<=A[m]){
temp[i]=A[l];
l++;
}
else{
temp[i]=A[m];
m++;
}
i++;
}
if(l>mid){
for(k=m;k<=last;k++){
temp[i]=arr[k];
i++;
}
}
else{
for(k=l;k<=mid;k++){
temp[i]=arr[k];
i++;
}
}
for(k=first;k<=last;k++){
A[k]=temp[k];
}
}
Output : Enter the total number of elements: 5 Enter the elements which to be sort: 3 1 6 4 7 After merge sorting elements are: 1 3 4 6 7Complexity of Merge Sort :(8) T(2) / 2 = T(1) / 1 + 1 Adding equations (3) through (8), the sum of their left–hand sides will be equal to the sum of their right–hand sides:T(N) / N + T(N/2) / (N/2) + T(N/4) / (N/4) + … + T(2)/2 = T(N/2) / (N/2) + T(N/4) / (N/4) + ….+ T(2) / 2 + T(1) / 1 + LogN(LogN is the sum of 1s in the right–hand sides) After crossing the equal term, we get (9) T(N)/N = T(1)/1 + LogN T(1) is 1, hence we obtain(10) T(N) = N + NlogN = O(NlogN) Hence the complexity of the MergeSort algorithm is O(NlogN).
Quick Sort | Merge Sort |
An efficient sorting serving as a systematic method for placing the elements of an array in order | An efficient general purpose comparison based sorting algorithms |
Sorts the elements by comparing each element with the pivot | Divides the array into 2 subarrays again and again until one element is left |
Suitable for small arrays | Works for any type of array |
Works faster for small data sets | Works in consistent speed for all data sheets |
Requires minimum space | Requires more space |
Program for Merge Sort
#include<stdio.h>
#define MAX 50
void mergeSort(int A[],int first,intmid,int high);
void divide(int A[],int first,int last);
int main(){
int merge[MAX],i,n;
printf("Enter the total number of elements: ");
scanf("%d",&n);
printf("Enter the elements which to be sort: ");
for(i=0;i<n;i++){
scanf("%d",&merge[i]);
}
divide(merge,0,n–1);
printf("After merge sorting elements are: ");
for(i=0;i<n;i++){
printf("%d ",merge[i]);
}
return 0;
}
void divide(int A[],int first, int last)
{
int mid;
if(first<last){
mid=(first+last)/2;
divide(A,first,mid);
divide(A,mid+1,last);
mergeSort(A,first,mid,last);
}
}
void mergeSort(int A[],int first,intmid,int last)
{
int i,m,k,l,temp[MAX];
l=first;
i=first;
m=mid+1;
while((l<=mid)&&(m<=last)){
if(A[l]<=A[m]){
temp[i]=A[l];
l++;
}
else{
temp[i]=A[m];
m++;
}
i++;
}
if(l>mid){
for(k=m;k<=last;k++){
temp[i]=arr[k];
i++;
}
}
else{
for(k=l;k<=mid;k++){
temp[i]=arr[k];
i++;
}
}
for(k=first;k<=last;k++){
A[k]=temp[k];
}
}
Output : Enter the total number of elements: 5 Enter the elements which to be sort: 3 1 6 4 7 After merge sorting elements are: 1 3 4 6 7 Q8. Explain the complexity of merge sort?A8. Time to mergesort N elements = Time to mergesort N/2 elements plus time to merge two arrays each N/2 elements. Time to merge two arrays each N/2 elements is linear, i.e. N Thus we have: (1) T(1) = 1 (2) T(N) = 2T(N/2) + N Dividing (2) by N we get: (3) T(N) / N = T(N/2) / (N/2) + 1 N is a power of two, so we can write (4) T(N/2) / (N/2) = T(N/4) / (N/4) +1 (5) T(N/4) / (N/4) = T(N/8) / (N/8) +1 (6) T(N/8) / (N/8) = T(N/16) / (N/16) +1 (7) ……(8) T(2) / 2 = T(1) / 1 + 1 Adding equations (3) through (8), the sum of their left–hand sides will be equal to the sum of their right–hand sides:T(N) / N + T(N/2) / (N/2) + T(N/4) / (N/4) + … + T(2)/2 = T(N/2) / (N/2) + T(N/4) / (N/4) + ….+ T(2) / 2 + T(1) / 1 + LogN(LogN is the sum of 1s in the right–hand sides) After crossing the equal term, we get (9) T(N)/N = T(1)/1 + LogN T(1) is 1, hence we obtain(10) T(N) = N + NlogN = O(NlogN) Hence the complexity of the MergeSort algorithm is O(NlogN). Q9. Write a program for quick sort.A9.
Program for Quick Sort:
#include<stdio.h>
void quicksort(int A[10],int,int);
int main(){
int A[20],n,i;
printf("Enter size of the array: ");
scanf("%d",&n);
printf("Enter %d elements: ",n);
for(i=0;i<n;i++)
scanf("%d",&A[i]);
quicksort(A,0,n–1);
printf("Sorted elements: ");
for(i=0;i<n;i++)
printf(" %d",A[i]);
return 0;
}
void quicksort(int A[20],int first, int last)
{
int pivot,j,temp,i;
if(first<last){
pivot=first;
i=first;
j=last;
while(i<j){
while(A[i]<=A[pivot]&&i<last)
i++;
while(A[j]>A[pivot])
j––;
if(i<j){
temp=A[i];
A[i]=A[j];
A[j]=temp;
}
}
temp=A[pivot];
A[pivot]=A[j];
A[j]=temp;
quicksort(A,first,j–1);
quicksort(A,j+1,last);
}
}
Output : Enter size of the array: 5 Enter 5 elements: 3 8 0 1 2 Sorted elements: 0 1 2 3 8 Complexity of Quick Sort The time to sort the file is equal to