Unit 3
Interaction of Radiation with Materials
Q1. A domestic hot water tank (0.5 m diameter and 1 m high) is installed in a large space. The ambient temperature is 25°C. If the tank surface is oxidised copper with an emissivity of 0.8, find the heat loss from the tank surface at temperature 80°C by radiation. What would be the reduction in heat loss if a coating of aluminium paint having an emissivity of 0.3 is given to the tank? What would be the increase in heat loss if a white paint having an emissivity of 0.97 is given to the tank?
Q2. A black body emits radiation at 2000 K. Calculate (i) the monochromatic emissive power at 1 
m wavelength, (ii) wavelength at which the emission is maximum, and (iii) the maximum emissive power.
Q3. The filament of a 75 W light bulb may be considered a black body radiating into a black enclosure at 70°C. The fi lament diameter is 0.10 mm and length is 50 mm. Considering the radiation, deter mine the fi lament temperature.
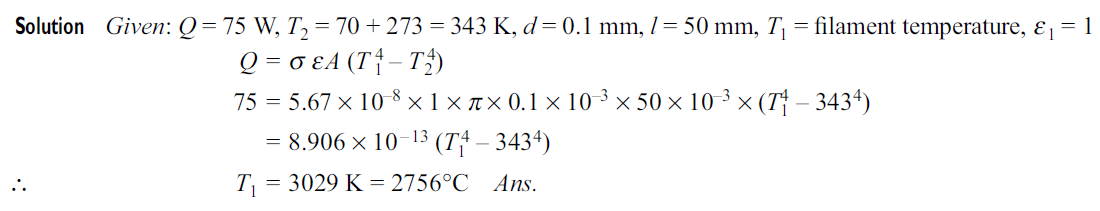
Q4. Assuming the sun as a black body, it emits maximum radiation at 0.5 
m wavelength. Calculate (i) the surface temperature of the sun, (ii) its emissive power, (iii) the energy received by the surface of the earth and (iv) the energy received by a 2 m 
2 m solar collector whose normal is inclined at 60° to the sun. Take the diameter of the sun as 1.4 
109 m, diameter of the earth as 13 
106 m and the distance of the earth from the sun as 15 
1010m.
Q5. A sphere of radius 5cm is concentric with another sphere. Find radius of outer sphere so that shape so that shape factor of outer sphere with respect inner sphere is 0.6.
A1=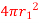
and A2=
F21=0.6
Sol: Since inside sphere is completely enclosed in outer sphere F11=0
By enclosure theorem
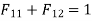
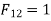
By reciprocating theorem
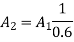
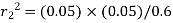
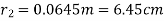
Q6. A double-walled thermos flask may be assumed to be equivalent to two infinite parallel plates. The emissivities of wall are 0.3 and 0.7 respectively. Space between them is evacuated. Find the heat transfer rate by radiation through the flask if inside surface temperature is 90oC and outside surface temperature at 30oC under steady state.
Sol:
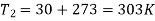
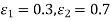
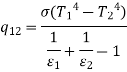
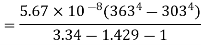
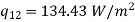
Q7. A spherical ball 6 cm in diameter and 310 K is placed inside a large spherical furnace at 600 K. Estimate the diameter of the spherical furnace such that 20% of the energy emitted by the furnace reaches the spherical ball. Assume the surfaces as black. What is the net exchange of energy between the two surfaces?
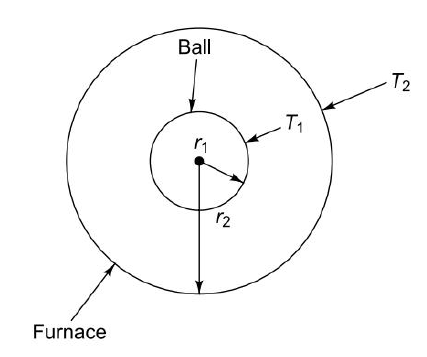
Fig.1
Q8. A small sphere (outside radius = 60 mm) with a surface temperature of 300°C is located at the geometric centre of a large sphere (inside diameter = 360 mm) with an inner surface temperature of 15°C. Calculate how much of heat emitted from the large sphere inner surface is incident upon the outer surface of the small sphere, assuming that both surfaces approach black body behavior. What is the net exchange of heat between the two spheres?
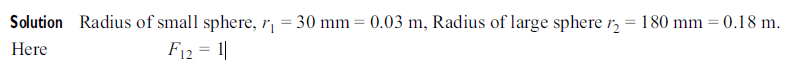
Q9. Explain and derive Stefan–Boltzmann Law
Sol: It states that total emissive power of black body is directly proportional to fourth power of absolute temperature.
Planck’s law also permits to derive Stefan–Boltzmann law, which establishes the dependence of total hemispherical radiation on temperature.
The total emissive power of a black body is given by
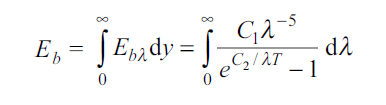
Substituting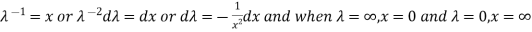 
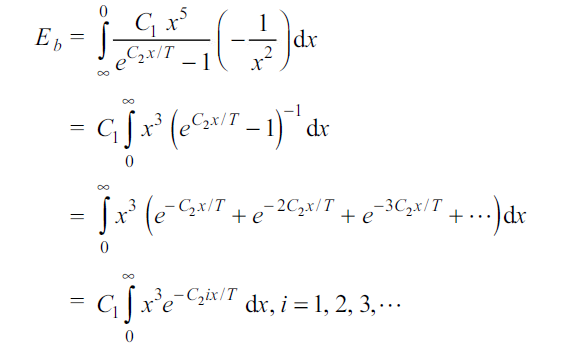
Since
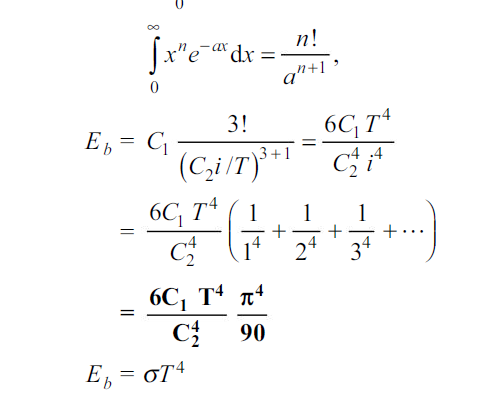
Where 
is the Stefan-Boltzmann constant.
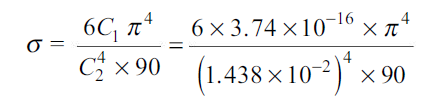
=5.67 X 10-8 W/m2 K4
Q10. Classify the bodies based on their radiative characteristics.
Sol:
It implies that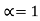
,
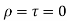
No perfect black body exist.
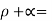
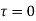
For such bodies 
