Module 01
Atomic and molecular structure
Q-1 Explain Plane Wave Equation.
Answer:
A wave is a disturbance of a physical quantity undergoing simple harmonic motion or oscillations about its place. The disturbance gets passed on to its neighbors in a sinusoidal form.

The equation for the wave is a second-order partial differential equation of a scalar variable in terms of one or more space variable and time variable. The one-dimensional wave equation is-
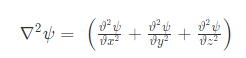
The amplitude (y) for example of a plane progressive sinusoidal wave is given by:
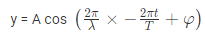
Where, A is the maximum amplitude, T is the period and φ is the phase difference of the wave if any and t is the time in seconds. For a standing wave-
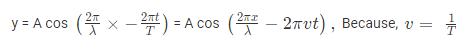
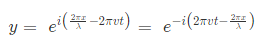
Q-2Enlist the importance of schrodinger wave equation.
Answer:
- The electronic structure of atoms and molecules can be well explained using the Schrodinger’s equation
- The solution of Schrodinger’s equation results in quantized properties of systems. E.g.: energy quantization. The quantization is a consequence of the periodic boundary conditions involved.
- Solving the Schrodinger’s equation for a solid is basically a many-body problem and it involves the solution of complex differential equations. The problem can be solved by expressing the differential Schrodinger’s equation in momentum space/reciprocal space, where the Schrodinger’s equation can be expressed as a set of linear algebraic equations rather than complex differential equations. Those linear equations can be solved using available computational numerical techniques accurately to predict the ground state properties of solids
- The solution of the Schrodinger’s equation in the reciprocal space gives the electronic band structure of solids.
- Most of the semiconductor properties such as the origin of energy band gap, the behavior of dopants and their energy levels present in relation to the observed band structure etc., can be well studied by solving the Schrodinger’s equation.
- Today it is possible to obtain a suitable dopant for a given semiconductor just by solving the corresponding Schrodinger’s equation, without conducting any experiments
Q-3Explain H2 molecule.
Answer:
H2 molecule
H2 molecule consist of two H atoms and their two electrons. Two 1s orbitals give two MOs- one bonding that is σ and another one is antibonding that is σ*. The bonding orbital is in lower in energy state, the two electron occupies the bonding MO. The MO electron configuration of H2 molecule is written as (σ1s) 2.

Energy evolved =
[No. Of electron in BMO (-) + No. Of electron in Anti Bonding Molecular Orbital * (+)]
=2*(- ) + 0*(+ )
= -2
This evolved energy is called as stabilization energy.
The molecule is stable so it is diamagnetic.
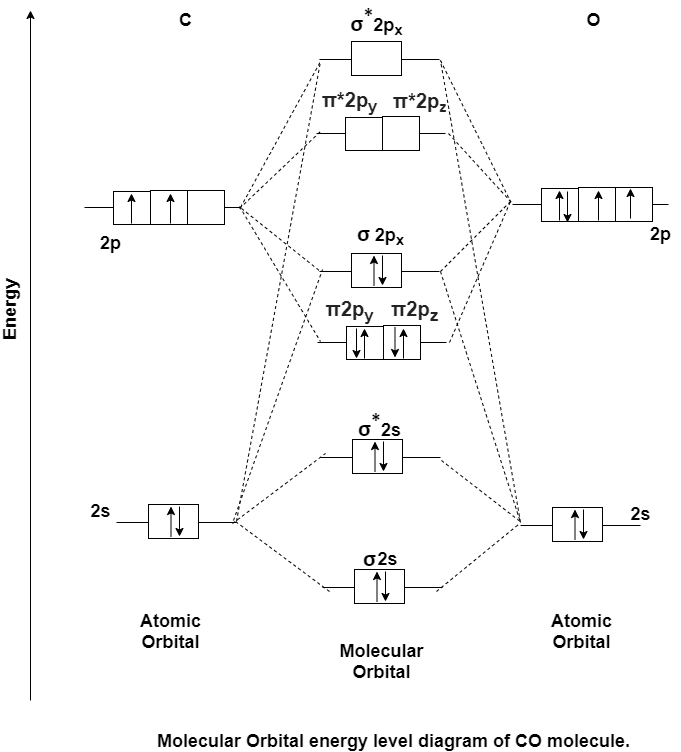
Q-4 Explain molecular structure of carbon monoxide.
Answer:
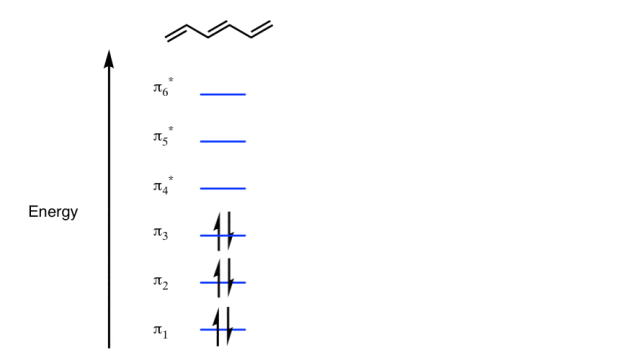
Q-5Explain Pi molecular orbital of butadiene.
Answer:
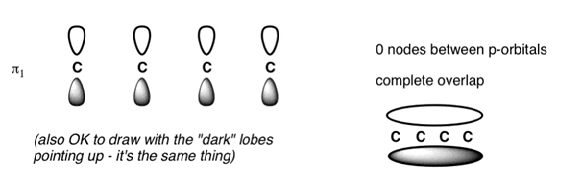
The Butadiene Pi System has zero nodes at its lowest energy molecular orbital.
The Butadiene Pi System has three nodes at its lowest energy molecular orbital. The drawn n-p orbital are at alternate phase to each other. This create the a pi system with three nodes.

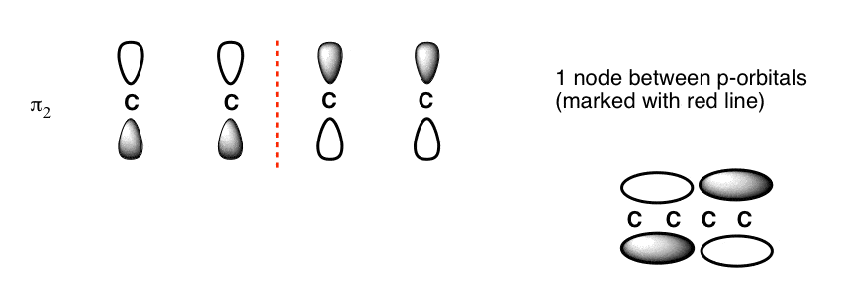
The Butadiene second lowest energy molecular orbital has one node.
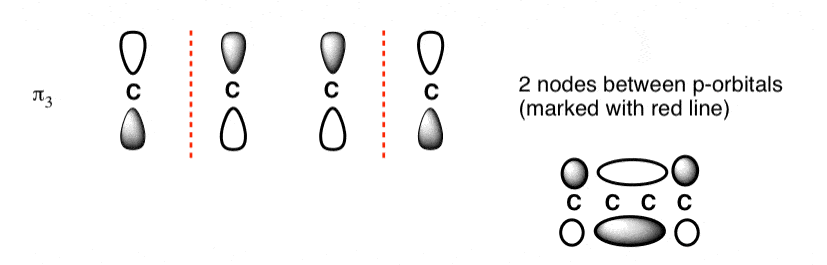
The third lowest energy molecular orbital has two nodes.
The Full Molecular Orbital Diagram for The Butadienyl System.
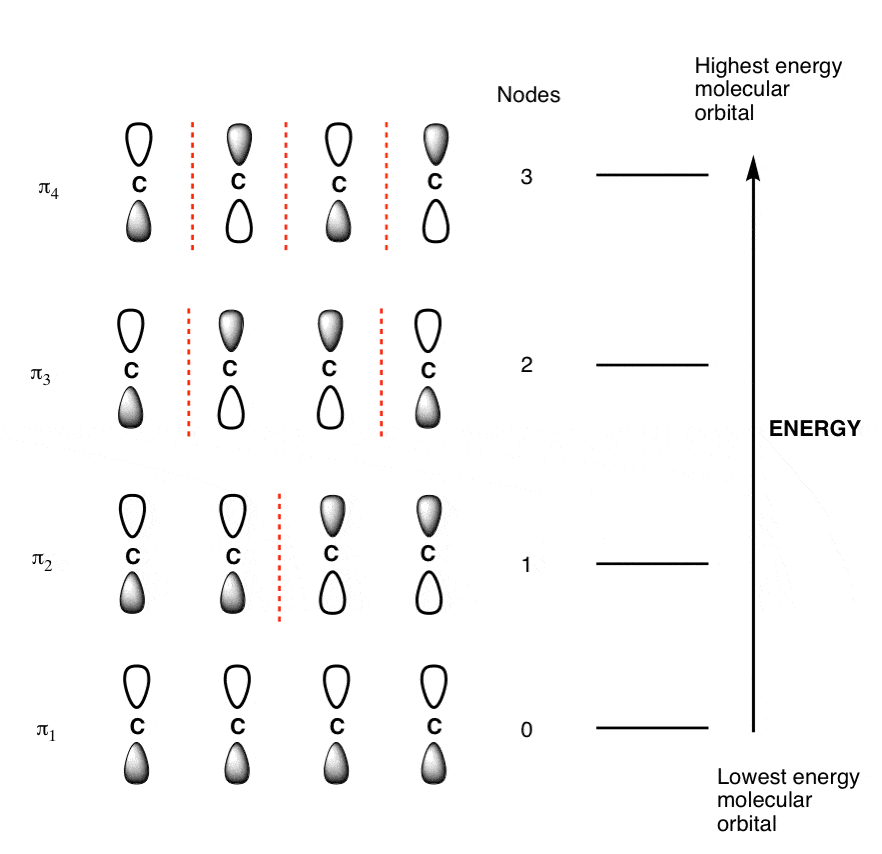
Populating the Molecular Orbital’s of Butadiene With Electrons

Q-6 Explain spectrochemical series.
Answer:
Spectrochemical Series: The ability of ligands to cause a large splitting of the energy between the orbital is essentially independent of the metal ion and the spectrochemical series is a list of ligands ranked in order of their ability to cause large orbital separations.
I- < Br- < SCN- ~Cl- < F- < OH- ~ ONO- < C2O42- < H2O< NCS- < EDTA4-<NH3 ~ pyr ~ en < bipy < phen < CN- ~ CO
Q-7Explain the crystal field theory of transition metal ion.
Answer:
D-Orbital Splitting
CFT focuses on the interaction of the five (n − 1)d orbital’s with ligands arranged in a regular array around a transition-metal ion. Other common structures, such as square planar complexes, can be treated as a distortion of the octahedral model.
According to CFT, an octahedral metal complex forms because of the electrostatic interaction of a positively charged metal ion with six negatively charged ligands or with the negative ends of dipoles associated with the six ligands. In addition, the ligands interact with one other electrostatically. According to VSEPR theory the lowest-energy arrangement of six identical negative charges is an octahedron, which minimizes repulsive interactions between the ligands.
The energies of the d-orbital of a transition-metal ion are affected by an octahedral arrangement of six negative charges. The five d-orbital are initially degenerate. On the distribution of six negative charges uniformly over the surface of a sphere, the d-orbital remain degenerate, but their energy will be higher due to repulsive electrostatic interactions between the spherical shell of negative charge and electrons in the d-orbital. Placing the six negative charges at the vertices of an octahedron does not change the average energy of the d-orbital, but it does remove their degeneracy: the five d-orbital split into two groups whose energies depend on their orientations. The dz2 and dx2−y2 orbital point directly at the six negative charges located on the x, y, and z axes. Consequently, the energy of an electron in these two orbital will be greater than it will be for a spherical distribution of negative charge because of increased electrostatic repulsions. In contrast, the other three d orbital (dxy, dxz, and dyz, collectively called the t2g orbitals) are all oriented at a 45° angle to the coordinate axes, so they point between the six negative charges. The energy of an electron in any of these three orbital is lower than the energy for a spherical distribution of negative charge.

Q-8Explain the magnetic property of transition metal ions.
Answer:
A magnetic field is generated due to the orbital motion and spin of the electron. The spinning of an electron in an orbit is very much similar to flow of electric current in a closed circuit. Therefore, an unpaired electron is regarded as a micro magnet which has a definite magnetic moment. A substance which contains an unpaired electron when placed in a magnetic field interacts with the applied field. Consequently, an attractive force is exerted and the paramagnetic property is shown. The number of unpaired electrons determines the magnitude of magnetic moment. Higher the number of unpaired electrons more is the magnetic moment and greater will be the paramagnetic behavior of the substance.
In the case of paired electrons, the electrons in each pair will have opposite spin. The magnetic field created by the electrons of same pair is equal and opposite in nature. Hence, the magnetic field which is created by one electron is cancelled by the other. So the net effect of the magnetic moment is zero. These kinds of substances show diamagnetic property and are repelled by the applied magnetic field.
Q-9 Explain the forbidden band.
Answer:
The energy gap between the valence band and the conduction band is known as the forbidden band which is also known as the forbidden gap. The electrical conductivity of a solid is determined from the forbidden gap and also the classification of the materials as conductors, semiconductors, and insulators.

Q-10Explain the Pi molecular orbital of benzene.
Answer:
The Pi molecular orbital diagram for Benzene
In the above increasing energy level the bottom three orbital are all bonding orbital while the top 3 orbital are anti bonding orbital.
The Benzene System has zero nodes at its lowest energy molecular orbital.

- All p orbital are aligned with phases pointing in the same direction.
- Nodes are absent between orbital.
- In this orbital, electrons are delocalized over the length of molecule, resulting in greatest lowering of energy.
Benzene Has Nodal Planes. The Maximum Energy Level Has 3 Nodal Planes

This orbital has zero overlap between adjacent p orbitals and therefore electrons in this orbital have the minimum possible delocalization. They are therefore the highest energy.

The pi molecular orbital of benzene