Question Bank
Unit-2
Question-1: If a continuous random variable X has the following probability density function:
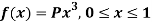
Then find-
1. P[0.2 < X < 0.5]
Solution:
Here f(x) is the probability density function, then-


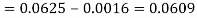
Question-2: The pdf of a continuous random variable is given as below-
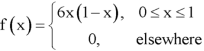
Then find the c.d.f. Of X.
Solution:
The c.d.f. Of X will be given by-
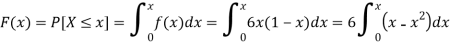

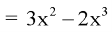
Hence the c.d.f will be-

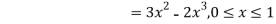
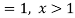
Question-3: :Following probability distribution
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P(x) | 0 |  | 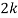 | 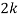 | 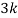 | 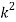 |  |  |
Find: (i) k (ii) 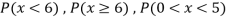
(i) Distribution function
(ii) If 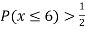 find minimum value of C
find minimum value of C
(iii) Find 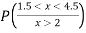
Solution:
If P(x) is p.m.f –
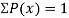
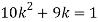
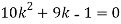
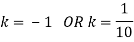
(i)
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P(x) | 0 | 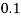 | 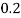 |  | 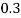 | 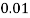 | 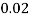 | 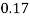 |
(ii)
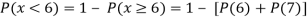
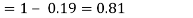

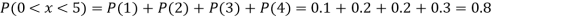
(iii)
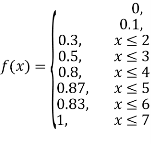
(iv)
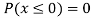
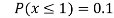
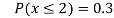
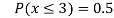
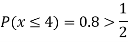
(v)
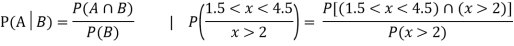
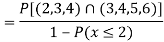
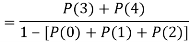
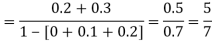
Question-4: Let  be two independent N(0,1) random variables. Define
be two independent N(0,1) random variables. Define
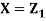
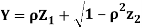
Where 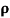 is a real number in (-1,1)
is a real number in (-1,1)
a. Show that X and Y are bivariate normal.
b. Find the joint PDF of X and Y.
c. Find 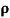 (X,Y)
(X,Y)
Sol. First, note that since 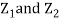 are normal and independent , they are jointly normal with the joint PDF
are normal and independent , they are jointly normal with the joint PDF
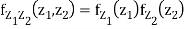
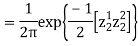
We need to show aX+bY is normal for all 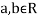 we have
we have


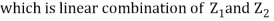 and thus it is normal.
and thus it is normal.
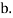 We can use the methods of transformations (Theorem 5.1) to find the joint PDF of X and Y . The inverse transformation is given by
We can use the methods of transformations (Theorem 5.1) to find the joint PDF of X and Y . The inverse transformation is given by
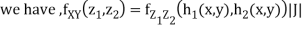
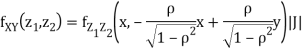
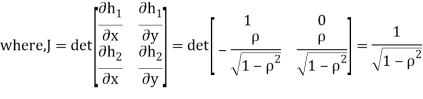
Thus we conclude that,


 To find
To find 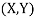 , first mode
, first mode

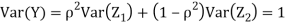
Therefore,
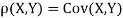

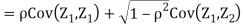
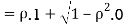
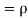
Question-5: Let X and Y be jointly normal random variables with parameters  Find the conditional distribution of Y given X =x.
Find the conditional distribution of Y given X =x.
Solution:
One way to solve this problem is by using the joint PDF formula since X N
N 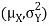 we can use
we can use
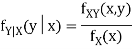
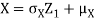
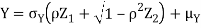
Thus given X=x, we have
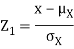
And,
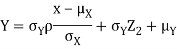
Since 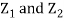 are independent, knowing
are independent, knowing 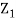 does not provide any information on
does not provide any information on 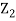 . We have shown that given X=x,Y is a linear function of
. We have shown that given X=x,Y is a linear function of  , thus it is normal. Ln particular
, thus it is normal. Ln particular
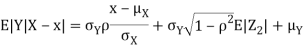
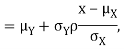

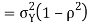
We conclude that given X=x,Y is normally distributed with mean 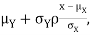 and variance
and variance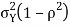
Question-6: Let X and Y be jointly normal random variables with parameters 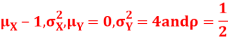
Find 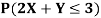
Find 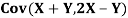
Find 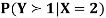
Solution:
a. Since X and Y are jointly normal, the random variable V-2X+Y is normal. We have
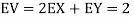
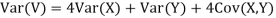
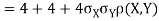
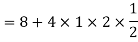
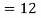
Thus, 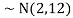 , therefore,
, therefore,
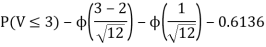
Note that 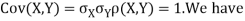
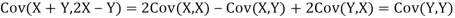
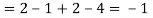
Using Properties, we conclude that given X=2,Y is normally distributed with

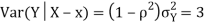
Thus,
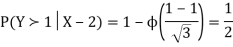
Question-7: A die is tossed thrice. A success is getting 1 or 6 on a toss. Find the mean and variance of the number of successes.
Solution:
Probability of mean success =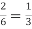
Probability of failures=
Probability of no success =Probability of all 3 failures =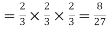
Probability of one success and 2 failures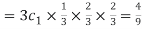
Probability of two success and one failure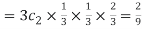
Probability of three successes 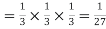
Now,
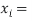 0 1 2 3
0 1 2 3
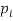 =8/27 4/9 2/9 1/27
=8/27 4/9 2/9 1/27
Mean,
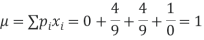
Also,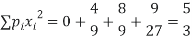
Variance,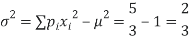
Question-8: The probability density function of a variate X is
X 0 1 2 3 4 5 6
P(X) k 3k 5k 7k 9k 11k 13k
(i) Find 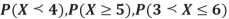
(ii) What will be the minimum value of k so that 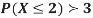 .
.
Solution:
(i) If X is a random variable, then
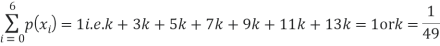
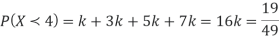
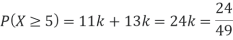

(ii) 
Thus minimum value of k 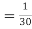
Question-9: A random variable X has the following probability function
x: 0 1 2 3 4 5 6 7
p(x) 0 k 2k 2k 3k 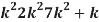
(i) Find the value of k.
(ii) Evaluate 
(iii) 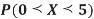
Solution:
(i) If X is a random variable then

i.e. 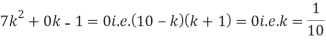
(ii) 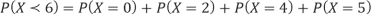
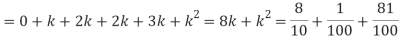
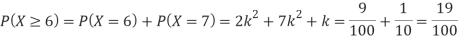
(iii)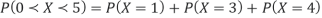
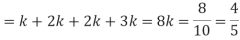
Question-10: A bag contains 12 pens of which 4 are defective. Three pens are picked at random from the bag one after the other.
Then find the probability that all three are non-defective.
Solution:
Here the probability of the first which will be non-defective = 8/12
By the multiplication theorem of probability,
If we draw pens one after the other then the required probability will be-

Question-11: The probability of A hits the target is 1 / 4 and the probability that B hits the target is 2/ 5. If both shoot the target then find the probability that at least one of them hits the target.
Solution:
Here it is given that-
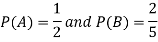
Now we have to find- 
Both two events are independent. So that-
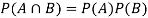

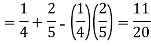
Question-12: An urn I contains 3 white and 4 red balls and an urn II contains 5 white and6 red balls. One ball is drawn at random from one of the urns and is found to be white.
Find the probability that it was drawn from urn I.
Solution:
Let
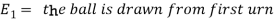


Now we have to find-
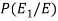
So that by using Bayes theorem, we get-
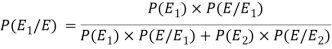
Here,
Two urns are equally likely to select,
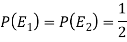

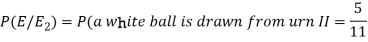
So that-
