UNIT-4
Question-1: Define large sample test for a proportion.
Sol.
Large Sample Test for a Proportion
- The sampling distribution of
 is approximately normal.
is approximately normal. - Use the value of p in the null hypothesis when computing the standard deviation of
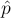 .
. - The test statistic is
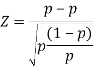
Hypothesis Test: Difference Between Proportions
This lesson describes how to conduct a hypothesis test to define whether the difference between two proportions is significant.
The test procedure, called the two-proportion z-test, is suitable when the following conditions are met:
- The sampling method for each population is simple random sample.
- The examples are independent.
- Each example comprises at least 10 attainments and 10 failures.
- Each population is at least 20 times as big as its example.
This approach contains of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results
Question-2: Define difference of proportions.
Sol.
To estimate the difference between two population proportions with a confidence interval, you can use the Central Limit Theorem when the sample sizes are large enough (typically, each at least 30). When a statistical characteristic, such as opinion on an issue (support/don’t support), of the two groups being compared is categorical, people want to report on the differences between the two population proportions — for example, the difference between the proportion of women and men who support a four-day work week. How do you do this?
You estimate the difference between two population proportions, p1 – p2, by taking a sample from each population and using the difference of the two sample proportions,
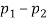
Plus or minus a margin of error. The result is called a confidence interval for the difference of two population proportions, p1 – p2.
The formula for a confidence interval (CI) for the difference between two population proportions is

And n1 are the sample proportion and sample size of the first sample, and 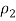

And n2 are the sample proportion and sample size of the second sample. The value z* is the appropriate value from the standard normal distribution for your desired confidence level. (Refer to the following table for z*-values.)
z*–values for Various Confidence Levels
Confidence Level | z*-value |
80% | 1.28 |
90% | 1.645 (by convention) |
95% | 1.96 |
98% | 2.33 |
99% | 2.58 |
To calculate a CI for the difference between two population proportions, do the following:
- Determine the confidence level and find the appropriate z*-value.
Refer to the above table.
2. Find the sample proportion
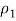
For the first sample by taking the total number from the first sample that are in the category of interest and dividing by the sample size, n1. Similarly, find 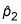 for the second sample.
for the second sample.
3. Take the difference between the sample proportions,
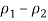
4. Find
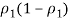
And divide that by n1. Find
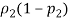
And divide that by n2. Add these two results together and take the square root.
5. Multiply z* times the result from Step 4.
This step gives you the margin of error.
6. Take
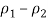
Plus or minus the margin of error from Step 5 to obtain the CI.
The lower end of the CI is

Minus the margin of error, and the upper end of the CI is
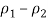
Plus the margin of error.
Question-3. What do you understand by single mean.
Sol.
The single mean (or one-sample) t-test is used to compare the mean of a variable in a sample of data to a (hypothesized) mean in the population from which our sample data are drawn. This is important because we seldom have access to data for an entire population. The hypothesized value in the population is specified in the Comparison value box.
We can perform either a one-sided test (i.e., less than or greater than) or a two-sided test (see the Alternative hypothesis dropdown). We use one-sided tests to evaluate if the available data provide evidence that the sample mean is larger (or smaller) than the comparison value (i.e., the population value in the null-hypothesis)
Question-4: Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
Sol. We compute the mean and the S.D. Of the difference between the marks of the two tests as under:
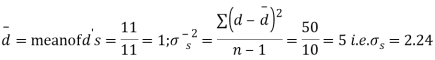
Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.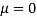
Then, 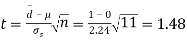 nearly and df v=11-1=10
nearly and df v=11-1=10
Students |  | 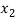 | 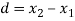 | 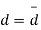 | 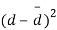 |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
|  |
| 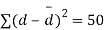 |
From table IV, we find that 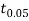 (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of 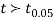 , the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Example-5: From a random sample of 10 pigs fed on diet A, the increase in weight in certain period were 10,6,16,17,13,12,8,14,15,9 lbs. For another random sample of 12 pigs fed on diet B, the increase in the same period were 7,13,22,15,12,14,18,8,21,23,10,17 lbs. Test whether diets A and B differ significantly as regards their effect on increases in weight ?
Sol. We calculate the means and standard derivations of the samples as follows
| Diet A |
|
| Diet B |
|
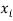 | 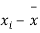 | 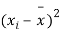 | 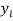 | 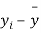 | 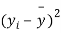 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
|
|
|
|
|
|
120 |
|
| 180 | 0 | 314 |
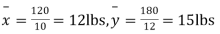



Assuming that the samples do not differ in weight so far as the two diets are concerned i.e. 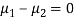
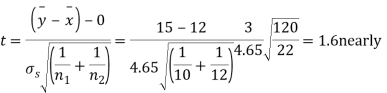
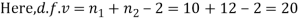
For v=20, we find  =2.09
=2.09
The calculated value of 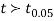
Hence the difference between the samples means is not significant i.e. thew two diets do not differ significantly as regards their effects on increase in weight.
Question-6: Explain test for single mean.
Sol.
When you test a single mean, you’re comparing the mean value to some other hypothesized value. Which test you run depends on if you know the population standard deviation (σ) or not.
Known population standard deviation
If you know the value for σ, then the population mean has a normal distribution: use a one sample z-test. The z-test uses a formula to find a z-score, which you compare against a critical value found in a z-table. The formula is:
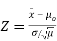
A one sample test of means compares the mean of a sample to a pre-specified value and tests for a deviation from that value. For example we might know that the average birth weight for white babies in the US is 3,410 grams and wish to compare the average birth weight of a sample of black babies to this value.
Assumptions
- Independent observations.
- The population from which the data is sampled is normally distributed.
Hypothesis:

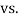
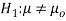
Where μ0 is a pre-specified value (in our case this would be 3,410 grams).
Test Statistic
- First calculate
 , the sample mean.
, the sample mean. - We choose an α = 0.05 significance level
- If the standard deviation is known:

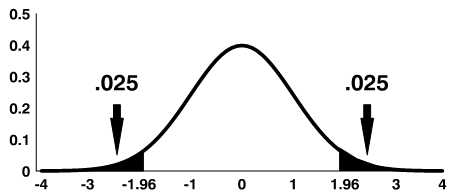
Using the significance level of 0.05, we reject the null hypothesis if z is greater than 1.96 or less than -1.96.
- If the standard deviation is unknown:
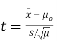
Using the significance level of 0.05, we reject the null hypothesis if |t| is greater than the critical value from a t-distribution with df = n-1.
Note: The shaded area is referred to as the critical region or rejection region.
We can also calculate a 95% confidence interval around the mean. The general form for a confidence interval around the mean, if σ is unknown, is
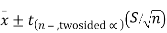
For a two-sided 95% confidence interval, use the table of the t-distribution (found at the end of the section) to select the appropriate critical value of t for the two-sided α=0.05.
Question-7: Explain difference for means and correlation coefficients.
Sol.
Testing the meaning of the correlation coefficient.
The relationship coefficient, r, tells us about the strength and direction of the linear relationship between X1 and X2.
Sample data is used to calculate r, the correlation coefficient for the sample. If we had data for the entire population, we could find the correlation coefficient for the population.
But since we only have sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, r, is our estimate of the correlation coefficient for the unknown population.
• ρ = population correlation coefficient (unknown)
• r = sample relationship coefficient (known; calculated from sample data)
The hypothesis test allows us to decide if the value of the population correlation coefficient ρ is "close to zero" or "significantly different from zero". We decide on the basis of the correlation coefficient of sample r and the size of sample n.
If the test arranges that the relationship coefficient is meaningfully different from zero, we say that the relationship coefficient is "significant".
• Conclusion: there is sufficient evidence to conclude that there is a significant linear relationship between X1 and X2 because the correlation coefficient is significantly different from zero.
Question-8: Explain Chi-square test.
The test is useful when you have two definite variables from a single population.
It is used to determine if there is a significant association between the two variables.
For example, in an electoral poll, voters could be classified by gender (male or female) and voting preference (democratic, republican, or independent).
We could use a chi-square test for independence to determine if gender is linked to voting preference. The example problem at the end of the lesson considers this example.
When to use the Chi-square test for independence
The testing procedure described in this lesson is appropriate when the following conditions are true:
The sample method is a simple random sampling.
The variables under consideration are categorical.
If the sample data is showed in a likelihood table, the predictable frequency total for each cell in the table is at least 5.
This approach involves four phases: (1) declaring the hypotheses, (2) formulating an analysis plan, (3) analyzing the sample data, and (4) interpreting the results.
State hypotheses
Suppose that variable A has levels r and that variable B has levels c. The null hypothesis establishes that knowing the level of variable A does not help to predict the level of variable B.
That is, the variables are independent.
Ho: variable A and variable B are independent.
Ha: variables A and B are not independent.
The another hypothesis is that meaningful the level of flexible A can help you expect the level of variable B.
Note: support for the another hypothesis proposes that the variables are connected; but the connection is not essentiallyconnecting, in the sense that one variable "causes" the other.
Formulate an analysis plan.
The analysis plan describes how to use the sample data to accept or reject the null hypothesis. The plan must specify the following elements.
Level of significance. Researchers often choose significance levels of 0.01, 0.05, or 0.10; but you can use any value between 0 and 1.
Test method. Use the chi-square test to determine independence to determine if there is a significant relationship between two categorical variables.
Analyze the sample data.
Using the sample data, find the degrees of freedom, the predictable frequencies, the test statistic, and the P value associated with the test statistic. The methoddefined in this unit is showed in the sample problematic at the end of this lesson.
Degrees of freedom. The degrees of freedom (DF) are equal to:
DF = (r - 1) * (c - 1)
Where r is the number of levels for one catabolic variable and c is the number of levels for the other categorical variable.
You predictable frequencies. The predictable frequency counts are considereddistinctly for each level of one definite variable at each level of the other categorical variable.
Calculate the predictable frequencies r * c, according to the following formula.
Er, c = (nr * nc) / n
Where Er, c is the predictable frequency count for level r of variable A and level c of variable B, nr is the total number of sample explanations at level r of variable A, nc is the total number of sample explanations at level c of variable B, en is the total sample size.
Statistical test. The test statistic is a chi-square (Χ2) random variable defined by the following equation.
Χ2 = Σ[ (Or,c - Er,c)2 / Er,c ]
Where O, c is the observed frequency count at level r of variable A and level c of variable B, and Er, c is the predicted frequency count at level r of adjustable A and level c of adjustable B.
p-value The P value is the probability of detecting a sample figure as exciting as the test statistic.
Meanwhile the test measurement is a chi-square, use the Chi-square supply calculator to measure the probability related with the test statistic. Use the degrees of freedom considered above.
Interpretation of results
If the sample results are unlikely, given the null hypothesis, the researcher rejects the null hypothesis.
Typically, this involves comparing the P value with the significance level and rejecting the null hypothesis when the P value is less than the significance level.
Question-9: A public opinion poll analyzed a simple random sample of 1,000 voters. Respondents were classified by gender (male or female) and by voting preference (Republican, Democratic, or Independent).
The effects are shown in the possibility table below.
| Voting Preferences | Row total | ||
Rep | Dem | Ind | ||
Male | 200 | 150 | 50 | 400 |
Female | 250 | 300 | 50 | 600 |
Column total | 450 | 450 | 100 | 1000 |
- Is there a gender gap? Do men's voting preferences differ significantly from women's preferences? Use a significance level of 0.05. Solution The solution to this problem involves four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze the sample data, and (4) interpret the results.
- We work through the following steps:
State the hypotheses. The first step is to affirm the null hypothesis and an alternative hypothesis. Ho: Gender and voting preferences are independent. Ha: Gender and voting preferences are not independent.
Formulate an analysis plan. For this analysis, the significance level is 0.05. Using sample data, we will perform a chi-square test for independence.
Analyze the sample data. By applying the chi-square test for independence to the sampling data, we calculated degrees of freedom, predictable frequency counts, and chi-square test statistics.
Based on the chi-square statistic and the degrees of freedom, we determine the value P..
DF = (r - 1) * (c - 1) = (2 - 1) * (3 - 1) = 2
Er,c = (nr * nc) / n
E1,1 = (400 * 450) / 1000 = 180000/1000 = 180
E1,2 = (400 * 450) / 1000 = 180000/1000 = 180
E1,3 = (400 * 100) / 1000 = 40000/1000 = 40
E2,1 = (600 * 450) / 1000 = 270000/1000 = 270
E2,2 = (600 * 450) / 1000 = 270000/1000 = 270
E2,3 = (600 * 100) / 1000 = 60000/1000 = 60
Χ2 = Σ [ (Or,c - Er,c)2 / Er,c ]
Χ2 = (200 - 180)2/180 + (150 - 180)2/180 + (50 - 40)2/40
+ (250 - 270)2/270 + (300 - 270)2/270 + (50 - 60)2/60
Χ2 = 400/180 + 900/180 + 100/40 + 400/270 + 900/270 + 100/60
Χ2 = 2.22 + 5.00 + 2.50 + 1.48 + 3.33 + 1.67 = 16.2
Where DF is the degree of freedom, r is the number of levels of gender, c is the number of levels of the voting preference, nr is the number of observations of level r of gender, nc is the number of observations of level c of voting preference, n is the number of observations in the sample, Er, c is the predicted frequency count when gender is level r and voting preference is level c, and O, c is the observed frequency count when gender is level r, voting preference is level c.
The P value is the probability that a chi-square statistic with 2 degrees of freedom is more extreme than 16.2.
We use the Chi-Square distribution calculator to find P (Χ2> 16.2) = 0.0003.
Interpret the results. Since the P value (0.0003) is lower than the significance level (0.05), we cannot accept the null hypothesis.
Therefore, we conclude that there is a relationship between gender and voting preference.