Question Bank
Module – 1
Basic Probability
Question-1: A bag contains 7 red and 8 black balls then find the probability of getting a red ball.
Solution:
Here total cases = 7 + 8 = 15
According to the definition of probability,
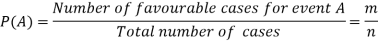
So that, here favourable cases- red balls = 7
Then,
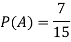
Question-2: A box contains 4 white and 2 black balls and a second box contains three balls of each colour. Now a bag is selected at random and a ball is drawn randomly from the chosen box. Then what will be the probability that the ball is white.
Solution:
Here we have two mutually exclusive cases-
1. The first bag is chosen
2. The second bag is chosen
The chance of choosing the first bag is 1/2. And if this bag is chosen then the probability of drawing a white ball is 4/6.
So that the probability of drawing a white ball from first bag is-
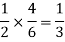
And the probability of drawing a white ball from second bag is-
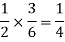
Here the events are mutually exclusive, then the required probability is-
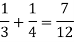
Qustion-3: 25 lottery tickets are marked with first 25 numerals. A ticket is drawn at random.
Find the probability that it is a multiple of 5 or 7.
Solution:
Let A be the event that the drawn ticket bears a number multiple of 5 and B be the event that it bears a number multiple of 7.
So that
A = {5, 10, 15, 20, 25}
B = {7, 14, 21}
Here, as A  B =
B =  ,
,
A and B are mutually exclusive
Then,
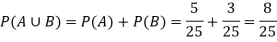
Question-4: A die is rolled. If the outcome is a number greater than three. What is the probability that it is a prime number?
Solution:
The sample space is- S = {1, 2, 3, 4, 5, 6}
Let A be the event that the outcome is a number which is greater than three and B be the event that it is a prime.
So that-
A = {4, 5, 6} and B = {2, 3, 5} and hence 
P(A) = 3/6, P(B) = 3/6 and 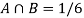
Now the required probability-


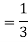
Question-5: Two cards are drawn from a pack of playing cards in succession with replacement of first card. Find the probability that the both are the cards of heart.
Solution:
Let A be the event that first card drawn is a heart and B be the event that second card is a heart card.
As the cards are drawn with replacement,
Here A and B are independent and the required probability will be-
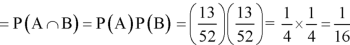
Question-6: Two male and female candidates appear in an interview for two positions in the same post. The probability that the male candidate is selected is 1/7 and the female candidate selected is 1/5.
What is the probability that-
1. Both of them will be selected
2. Only one of them will be selected
3. None of them will be selected.
Solution:
Here, P (male’s selection) = 1/7
And
P (female’s selection) = 1/5
Then-
1.

2.
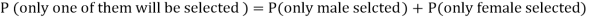

3.

Question-7: A can hit a target 3 times in 5 shots, B 2 times in 5 shots and C 3 times in 4 shots. All of them fire one shot each simultaneously at the target.
What is the probability that-
1. Two shots hit
2. At least two shots hit
Solution:
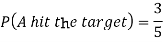
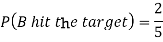
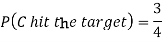
1. Now probability that 2 shots hit the target-

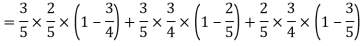
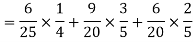

2.
Probability of at least two shots hitting the target
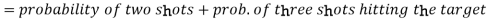

Question-8: The probability of A hits the target is 1 / 4 and the probability that B hits the target is 2/ 5. If both shoot the target then find the probability that at least one of them hits the target.
Solution:
Here it is given that-
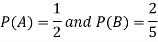
Now we have to find- 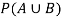
Both two events are independent. So that-


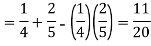
Question-9: A random variable x has the following probability distribution-

Then find-
1. Value of c.
2. P[X≤3]
3. P[1 < X <4]
Solution:
We know that for the given probability distribution-
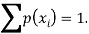
So that-
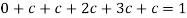
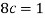

2.
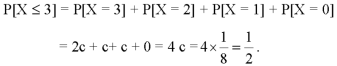
3.
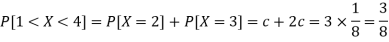
Question-10: Two discrete random variables X and Y have-
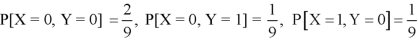
And
P[X = 1, Y = 1] = 5/9.
Check whether X and Y are independent or not?
Solution:
First we write the given distribution In tabular form-
X/Y | 0 | 1 | P(x) |
0 | 2/9 | 1/9 | 3/9 |
1 | 1/9 | 5/9 | 6/9 |
P(y) | 3/9 | 6/9 | 1 |
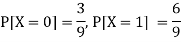
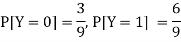
Now-
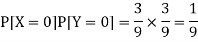
But
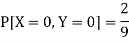
So that-
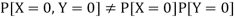
Hence X and Y are not independent.
Question-11: If we have 10 balls in a bag, in which 2 are red, 3 are green and remaining are blue colour balls. Then we select 4 balls randomly form the bag with replacement, then what will be the probability of selecting 2 green balls and 2 blue balls.
Solution:
Here this experiment has 4 trials so n = 4.
The required probability will be-
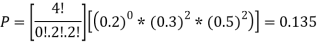
So that-
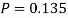
Question-12: A die weighed or loaded so that the number of spots X that appear on the up face when the die is rolled has pmf
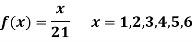
If this loaded die is rolled 21 times. Find the probability of rolling one one, two twos, three threes, four fours, five fives, six sixes.
Solution:
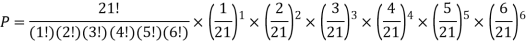
Question-13: A plant places biscuits into boxes of 100. The probability that a biscuit is cracked is 0.03. Find the probability that a box contains 2 cracked biscuits
Solution:
This is a binomial distribution by means of n = 100 besides p = 0.03.
These standards are external the range of the counters and include lengthy calculations.
Using the Poisson estimate (test: np = 100 x 0.3 = 3, which is less than 5)
Let X be the random variable of the number of cracked biscuits
The mean λ = np = 100 × 0.3 = 3
P(X = 2) = 0.224 (from counters)
The probability that a box contains two broken biscuits is 0.224.
Question-14: If the probability that a light bulb is defective is 0.8, what is the probability that the light bulb is not defective?
Solution:
Probability that the bulb is defective, p = 0.8
Probability that the bulb is not defective, q = 1 - p = 1 - 0.8 = 0.2
Question-15: 10 coins are tossed simultaneously where the probability of getting heads for each coin is 0.6. Find the probability of obtaining 4 heads.
Solution:
Probability of obtaining the head, p = 0.6
Probability of obtaining the head, q = 1 - p = 1 - 0.6 = 0.4
Probability of obtaining 4 of 10 heads, P (X = 4) = C104 (0.6) 4 (0.4) 6P (X = 4) = C410 (0.6) 4 (0.4) 6 = 0.111476736
Question-16: In an exam, 10 multiple-choice questions are asked where only one in four answers is correct. Find the probability of getting 5 out of 10 correct questions on an answer sheet.
Solution:
Probability of obtaining a correct answer, p = 1414 = 0.25
Probability of obtaining a correct answer, q = 1 - p = 1 - 0.25 = 0.75
Probability of obtaining 5 correct answers, P (X = 5) = C105 (0.25) 5 (0.75) 5C510 (0.25) 5 (0.75) 5 = 0.05839920044
Question-17: If a random variable X has the following probability distribution in tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | 1/2 | 1/4 |
Solution:
We know that-

So that-
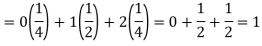
Question-18: Find the expectations of the number of an unbiased die when thrown.
Solution:
Let X be a random variable which represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-
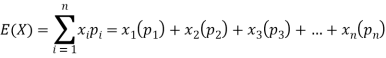
So that-
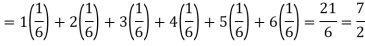
Question-19: Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
Solution:
x | y | 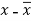 | 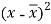 | 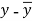 | 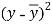 | ( 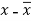  |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
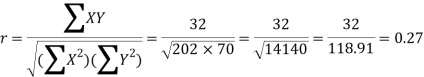
Question-20: A individual is selected from a population randomly who has average income of 40,000 dollars with SD 20,000 dollars, what will be the probability of selecting an individual whose income is either less than 10,000 dollars or greater than 70,000 dollars.
Solution:
Here we use Chebyshev inequality to solve such problems.
If X denotes income then X is less than 10,000 dollars or greater than 70,000 dollars only if-
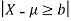
Where 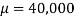 and b = 30,000 the the probability-
and b = 30,000 the the probability-
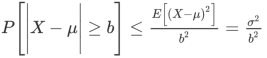
= 400,000,000/900,000,000 = 4/9