Unit – 3

Magnetic Circuits

Q1) Derive series magnetic current with air gap         

A1) In series magnetic circuit flux 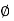is same in each part of circuit

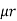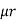Consider a composite magnetic circuit made from different material of lengths ɻ1,ɻ2, and ɻ3 cross sectional area a1, a2 And a3 and relative permeability’s  1 , 2 , 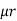3  resp. with an airgap of length ɻɡ

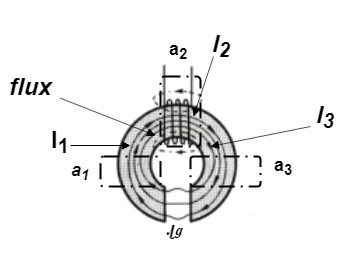
Total reluctance S = S1 + S2+ S3 + Sg

We know that S =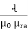

+ + +

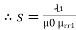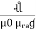
But S = 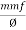and mmf = S x Ø

mmf = Ø + + 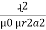+ 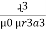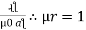for air

Now  B =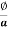 

mmȴ = + + +

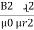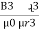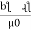
but B=μH

H =   = 

Total mmȴ = H1  ɻ1+ H2  ɻ2 + H3  ɻ3 + Hƪɻƪ

Q2) Explain a magnetic circuit which has more than one path for flux called parallel magnetic circuit

A2)

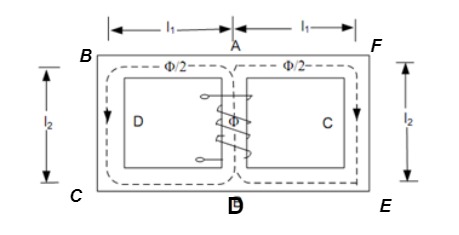
Mean length ABCDA = ɻ₁, and ADEFA = ɻ₂

Mean length path for central limb = ɻc

Reluctance ABCDA = S1, ADEFA = S2

And central limb = SC

Now total mmȴ = N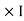

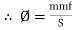i.e. mmf =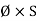

For path ABC AD

N =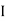

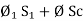
Where S1 =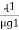 , S2 = 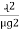, and Sc =

Where area of cross selection

for parallel ekt.

Total mmȴ = mmȴ by central limb + mmȴ required by any one of outer limb

       = Ø sc + [Ø1S1  or Ø2 S2]

As mmf across parallel branch is same

  Ø1 S1 = Ø2 S2

Hence while calculating total mmf, the mmf of only one of 2 parallel branches must be considered.

Q3) Explain Parallel Magnetic Circuits.

A3) A magnetic circuit which has more than one path for flux called parallel magnetic circuit

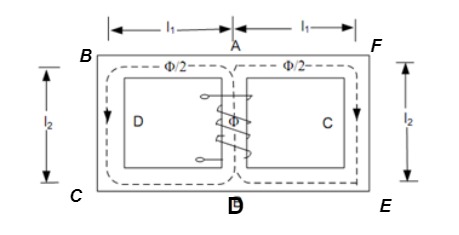
Mean length ABCDA = ɻ₁, and ADEFA = ɻ₂

Mean length path for central limb = ɻc

Reluctance ABCDA = S1, ADEFA = S2

And central limb = SC

Now total mmȴ = N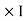

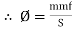i.e. mmf =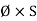

Q4) A magnetic circuit with a single air gap is shown in Figure. The core dimensions are:

A4) Cross-sectional area Ac = 1.8 × 10-3 m2

Mean core length lc = 0.6 m

Gap length g = 2.3 x 10-3 m

N = 83 turns 

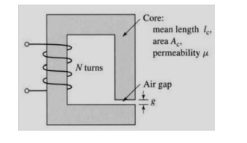
Assume that the core is of infinite permeability ( m -> ¥) and neglect the effects of fringing fields at the air gap and leakage flux. (a) Calculate the reluctance of the core Re and that of the gap Rg. For a current of i = 1.5 A, calculate (b) the total flux ϕ, (c) the flux linkages λ of the coil, and (d) the coil inductance L.

Solution:

Rc=0 since μ-> ∞

Rg = g/ μo Ac = 2.3 x 10 -3 / 4 π x 10 -7 x 1.8 x 10 -3 = 1.017 x 10 6 A/Wb

ɸ= Ni/ Rc + Rg = 83 x 1.5 / 1.017 x 10 6 = 1.224 x 10 -4 Wb

λ = N ɸ = 1.016 x 10 -2 Wb

 L = λ/i = 1.016 x 10 -2 / 1.5 = 6.773 mH

Q5) Consider the magnetic circuit of with the dimensions of Problem 1.1. Assuming infinite core permeability, calculate (a) the number of turns required to achieve an inductance of 12 mH and (b) the inductor current which will result in a core flux density of 1.0 T.

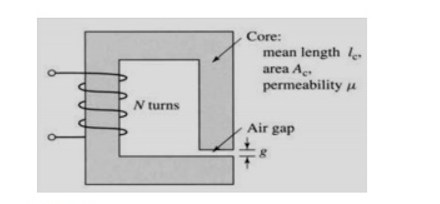
A5) L = N2 /Rg = 12 x 10 -3 mH

N = √ 12 x 10 -3 x 1.017 x 10 6 = 110.47 = 110 turns

Bc = Bg = 1.0 T

ɸ= Bg Ac = 1.8 x 10 -3 Wb

i = λ/L = N ɸ/L = 110 x 1.8 x 10 -3 / 12 x 10 -3 = 16.5 A

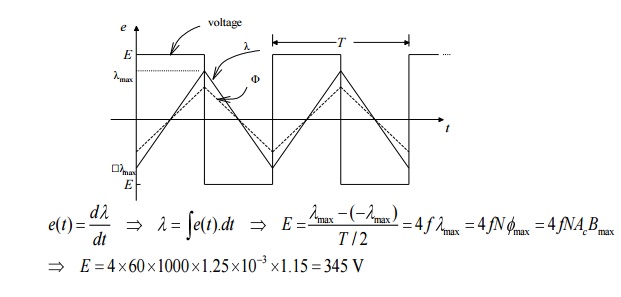
Q6) A square voltage wave having a fundamental frequency of 60 Hz and equal positive and negative half cycles of amplitude E is applied to a 1000-turn winding surrounding a closed iron core of 1.25 x 10-3m2 cross section. Neglect both the winding resistance and any effects of leakage flux.

(a) Sketch the voltage, the winding flux linkage, and the core flux as a function of time.

(b)Find the maximum permissible value of E if the maximum flux density is not to exceed 1.15 T.

 A6)

Q7) In the magnetic circuit as shown in figure (a) the relative permeability of the ferro magnetic material is 1200. Neglect the magnetic leakage and fringing. All dimensions are in centimetres, and the magnetic material has a square cross- sectional area. Determine the air gap flux , air gap flux density and the magnetic field intensity in the air gap.

A7) The mean magnetic path of the fluxes are shown by dashed lines in figure(a) The equivalent magnetic circuit is shown in figure(b).

F1 = N1 I1 = 500 x 10 = 5000 At

F2 = N2 I2 = 500 x 10 = 5000 At

μc= 1200 μo = 1200 x 4π x 10 -7

Rbafe = l bafe/ μc Ac

= 3 x 52 x 10 -2 / 1200 x 4π x 10 -7 x 4 x 10-4

= 2.58 x 10 6 At/Wb

Q8) For the magnetic circuit of the above figure N =400 turns.

Mean core length lc= 50 cm

Air gap length = 1.0 mm

Cross sectional area Ac = Ag = 15 cm2

Relative permeability of core μr = 3000

i = 1.0A

Find

A8)

Rc = lc / μr .μo. Ac = 50 x 10 -2 / 3000 x 4π x 10 -7 x 15 x 10 -4

= 88.42 x 10 3 AT/Wb

Rg = lg / μo Ag = 1 x 10 -3 / 4 π x 10 -7 x 15 x 10 -4

= 530.515 x 10 3   AT/Wb

ɸ = Ni/ Rc + Rg 

= 400 x 1.0 / (88.42 + 530.515 ) 10 3

B = ɸ/Ag = 0.6463 x 10 -3 / 15 x 10-4 = 0.4309

L = N2 / Rc + Rg = 400 2 / (88.42 + 530.515) 10 3

= 258.52 x 10  -3 H

Or

L = λ/i = Nɸ/i = 400 x 0.6463 x 10 -3 / 1.0 = 258.52 x 10 -3 H

Q9) Explain the application of series magnetic circuits?

A9) The most one we almost all see, are electronic lock systems. Some doors use solenoids to withdraw the bolt when you swipe your card, a magnetic circuit. Better door locks are strong electromagnets that hold a steel plate until the card is scanned. another magnetic circuit.