Unit – 1A
Calculus
Q1) Consider the sequence 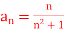 . You might intuitively understand that this sequence converges to zero as n goes to infinity. But we need to show this with a careful/rigorous mathematical argument.
. You might intuitively understand that this sequence converges to zero as n goes to infinity. But we need to show this with a careful/rigorous mathematical argument.
A1) Formal argument (this is what you would want to write and turn in) Let 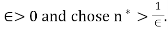 Then when n>
Then when n> 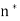 we have that
we have that
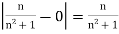
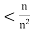
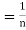

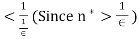
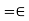
So, we have that 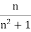 <
<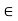 when n
when n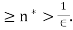 Therefore
Therefore 
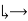 0 as n
0 as n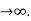
Q2) Show that 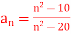 converges to 1.
converges to 1.
A2) We want  First notice that no n
First notice that no n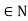 gives a zero in the denomination. Now simplify
gives a zero in the denomination. Now simplify 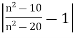 =
= so that we need to show
so that we need to show 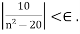 This is tricky because of the subtraction in the denominator. As long as n
This is tricky because of the subtraction in the denominator. As long as n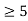 we have
we have 
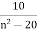 though. Now we just need to solve for n as a function of
though. Now we just need to solve for n as a function of 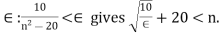 So as long as we choose a cut-off value
So as long as we choose a cut-off value 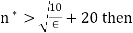 the argument will work… Almost
the argument will work… Almost
Remember that this calculation originally needed n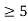 to keep the denominator positive. So we need satisfy
to keep the denominator positive. So we need satisfy 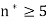 as well, and simultaneously satisfy
as well, and simultaneously satisfy 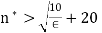 so that for any n
so that for any n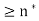 we have n
we have n And n>
And n> We solve this by choosing some
We solve this by choosing some
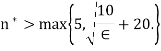
Let 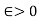 and choose some
and choose some
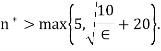
Then
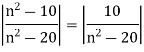
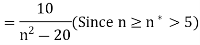
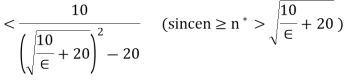
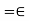
Thus 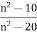 converges to 1.
converges to 1.
Q3) p-series test:
(a)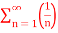 p =
p = 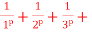 .........
.........
A3) Converges, if p>1
Diverges, if p<1
(b)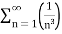 =
= 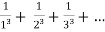
Here p = 3 so p>1 ,thus the given series converges.
 =
= 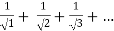
Here p= ie., p<1, thus the given series diverges
ie., p<1, thus the given series diverges
Q4) 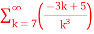
A4) 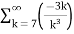 +
+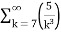
= -3.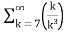 +5.
+5.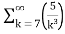
=-3.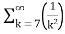 +5.
+5.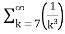
Therefore., here p=2 ,3 ie., p>1
Hence the given series converges.
Q5) Find the limit of the following points
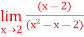
X | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 |
F(x) |
|
|
|
|
|
|
A5)
We apply the value of each x by finding the respective value through applying limits

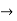 f(x)=
f(x)= 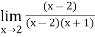
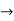 f(x)=
f(x)= 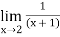
Finding limit at x= 1.9
f(x)= 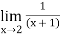
f(1.9)=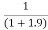
=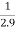
= 0.3448
Limit at x=1.99
f(1.99)= 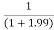
=
= 0.33444
Limit at x=1.999
f(1.999)= 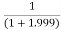
=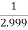
= 0.33344
Limit at x=2.001
f(2.001)= 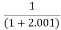
=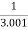
= 0.33322
Limit at x=2.01
f(2.01)= 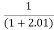
=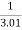
= 0.3225
From the above table we have to estimate the limit when x tends to 2
Here answer is 0.333....
Q6) Determine whether the following is dis-continuous at x=-1,0,
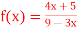
A6)
Given 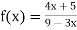
Verifying for continuity at x=-1
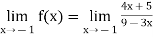
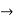

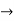

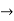
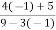
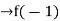
Therefore here 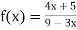 = f(-1)
= f(-1)
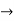 f(x)=f(-1)
f(x)=f(-1)
Hence the function is continuous at x=-1
Verifying at x=0
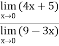
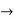
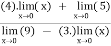
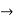
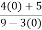
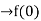
Therefore here 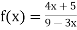 = f(0)
= f(0)
 f(x)=f(0)
f(x)=f(0)
Hence the function is continuous at x=0
Q7) 
A7) =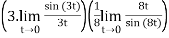
= (3) (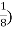
=
Q8) Consider the function f(x)=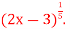 Discuss its continuity and differentiability at x=3/2
Discuss its continuity and differentiability at x=3/2
A8) For checking the continuity, we need to check the left hand and right-hand limits and the value of the function at a point x=a
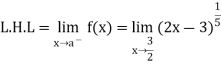
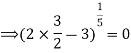
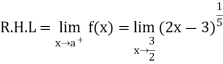
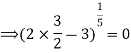
L.H.L = R.H.L = F(a) =0
Thus, the function is continuous at about the point x=3/2
Now to check differentiability at the given point, we know
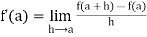
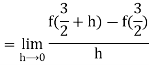
=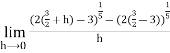
= 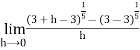
=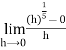
=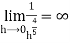
Thus, f is not differentiable at x=
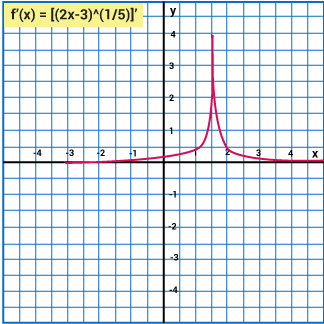
Q9) Test the differentiability of the function 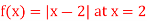
A9) We know that this function is continuous at x=2
But 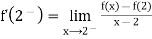
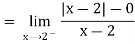
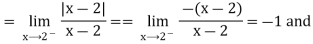

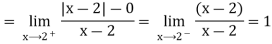
Since the one-sided derivatives 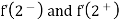 are not equal,
are not equal, 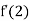 does not exist. That is, f is not differentiable at x=2. At all other points, the function differentiable.
does not exist. That is, f is not differentiable at x=2. At all other points, the function differentiable.
If 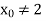 is any other point then
is any other point then

Thus
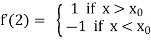
The fact that 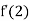 does not exist is reflected geometrically in the fact that the curve
does not exist is reflected geometrically in the fact that the curve 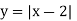 does not have a tangent line at (2,0). Note that the curve has a sharp edge at (2,0).
does not have a tangent line at (2,0). Note that the curve has a sharp edge at (2,0).
Q10) Verify Rolle’s theorem for the function f(x) = x2 for
A10) Here f(x) = x2;
i) Since f(x) is algebraic polynomial which is continuous in [-1, 1]
ii) Consider f(x) = x2
Diff. w.r.t. x we get
f'(x) = 2x
Clearly f’(x) exists in (-1, 1) and does not becomes infinite.
iii) Clearly
f(-1) = (-1)2 = 1
f(1) = (1)2 = 1
f(-1) = f(1).
Hence by Rolle’s theorem, there exist such that
f’(c) = 0
i.e. 2c = 0
c = 0
Thus, such that
f'(c) = 0
Hence Rolle’s Theorem is verified.
Q11) Verify Rolle’s Theorem for the function f(x) = ex (sin x – cos x) in
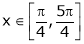
A11) Here f(x) = ex (sin x – cos x);
i) Ex is an exponential function continuous for every 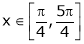 also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 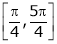 and Hence ex(sin x – cos x) is continuous in
and Hence ex(sin x – cos x) is continuous in  .
.
ii) Consider
f(x) = ex (sin x – cos x)
diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex [2sin x]
Clearly f’(x) is exist for each 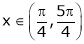 & f’(x) is not infinite.
& f’(x) is not infinite.
Hence f(x) is differentiable in 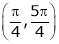 .
.
iii) Consider
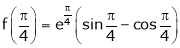
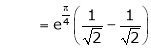
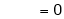
Also,
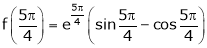

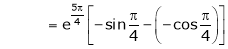
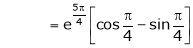
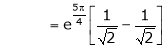

Thus 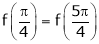
Hence all the conditions of Rolle’s theorem are satisfied, so there exist 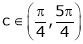 such, that
such, that
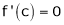
i.e. 
i.e. sin c = 0

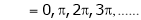
But

Hence Rolle’s theorem is verified
Q12) Verify the Lagrange’s mean value theorem for
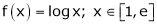
A12) Here 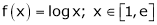
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
ii) Consider f(x) = log x.
Diff. w.r.t. x we get,
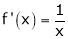
Clearly f’(x) exists for each value of 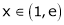 & is finite.
& is finite.
Hence all conditions of LMVT are satisfied Hence at least 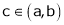
Such that
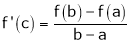
i.e. 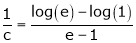
i.e. 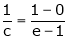
i.e. 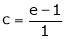
i.e. 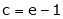
since e = 2.7183
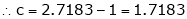
Clearly c = 1.7183 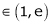
Hence LMVT is verified.
Q13) Verify mean value theorem for f(x) = tan-1x in [0, 1]
A13) Here 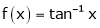 ;
; 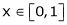
i) Clearly 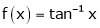 is an inverse trigonometric function and hence it is continuous in [0, 1]
is an inverse trigonometric function and hence it is continuous in [0, 1]
ii) Consider 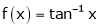
diff. w.r.t. x we get,
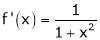
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist 
Such that
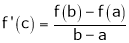
i.e. 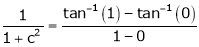
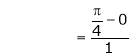
i.e. 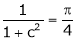
i.e. 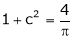
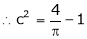
i.e. 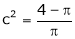
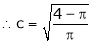
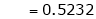
Clearly 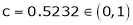
Hence LMVT is verified.
Q14) Find the taylor series for the following:
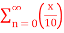
 =
= 
 <1
<1
A14) 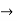 (x/10) <1 and (x/10) > -1
(x/10) <1 and (x/10) > -1
Therefore, radius of convergence is (-10,10)
 ROC =10
ROC =10
Q15) f(n)5 = 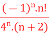
Here the ROC is 4
Compute the Taylor series centred at zero for f(x)= sinx
A15)
f(x)=sinx f (0) = 0
f’(x)=cosx f’ (0) =1
f’’(x)=-sinx f’’ (0) =0
f’’’(x)= -cosx f’’’ (0) =-1
f(4)(x) = cosx f(4) (0)= 1
Applying Taylor series, we get
T(x) =  =
= 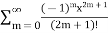 = x-
= x-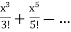
Thus, turns out to converge x to sinx.
Maclaurian series)
Q16)  (x)n
(x)n
A16) f(x)=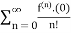
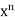
= f(0)+f’(0)x+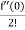 x2 +
x2 + 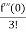 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 
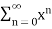
Q17) Find the Maclaurian series for f(x)= ex
A17) To get Maclaurian series, we look at the Taylor series polynomials for f near 0 and let them keep going.
Considering for example 
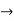
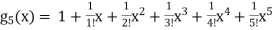
By Maclaurian series we get,
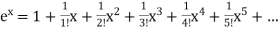 +
+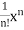
Q18) Evaluate
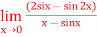
A18) 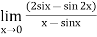
Differentiate the above form, we get

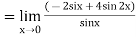
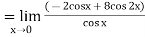
Now substitute the limit,
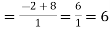
Therefore,
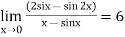
Q19) Evaluate

A19) Given,

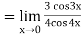
Now substitute the limit
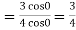
Therefore,
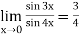
Q20) Find out the maxima and minima of the function
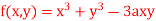
A20) Given 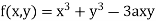 …(i)
…(i)
Partially differentiating (i) with respect to x we get
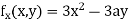 …. (ii)
…. (ii)
Partially differentiating (i) with respect to y we get
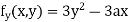 …. (iii)
…. (iii)
Now, form the equations 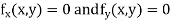
Using (ii) and (iii) we get
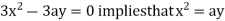
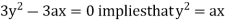
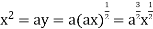 using above two equations
using above two equations
Squaring both sides, we get
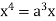
Or 
This show that 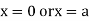
Also, we get 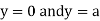
Thus, we get the pair of value as 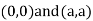
Now, we calculate
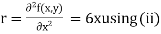
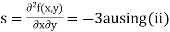
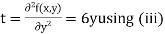
Putting above values in
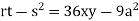
At point (0,0) we get
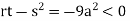
So, the point (0,0) is a saddle point.
At point 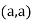 we get
we get
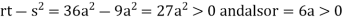
So, the point 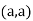 is the minimum point where
is the minimum point where 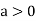
In case 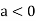
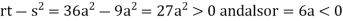
So, the point 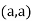 is the maximum point where
is the maximum point where 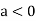
Q21) Find the maximum and minimum point of the function

A21) Partially differentiating given equation with respect to and x and y then equate them to zero


On solving above, we get 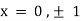
Also 
Thus, we get the pair of values (0,0), (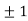 ,0) and (0,
,0) and (0,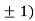
Now, we calculate
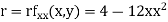
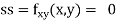
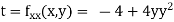
At the point (0,0)
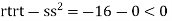
So, function has saddle point at (0,0).
At the point (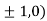
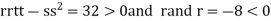
So, the function has maxima at this point (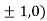 .
.
At the point (0,
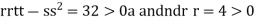
So, the function has minima at this point (0,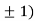 .
.
At the point (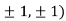
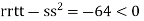
So, the function has an saddle point at (
Q22) Find the maximum and minimum value of 
A22) Let 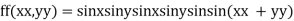
Partially differentiating given function with respect to x and y and equate it to zero
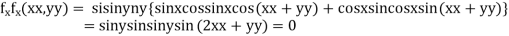 ...(i)
...(i)
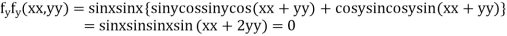 ...(ii)
...(ii)
On solving (i) and (ii) we get
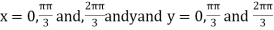
Thus, pair of values are 
Now, we calculate
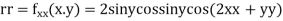

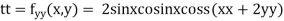
At the point (0,0)

So further investigation is required
On the x axis y = 0, f(x,0) =0
On the line y=x, 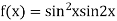
At the point 

So that the given function has maximum value at 
Therefore, maximum value of given function
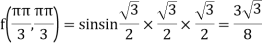
At the point 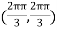

So that the given function has minimum value at 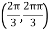
Therefore, minimum value of the given function
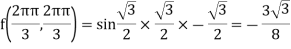
Q23) 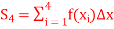
A23) From the given equation
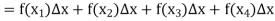
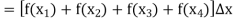
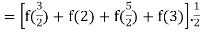
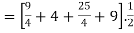
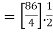

Q24) 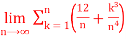
A24)
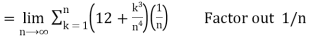



= 49/4.