Unit - 1B

Calculus

Q1) Find the area of the surface generated by rotating the function about the x-axis over

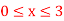  and the curve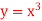

A1) We have the equation of the form y=f(x) and we are rotating around the x-axis, we’ll use the formula

S =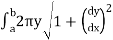

We will calculate 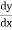and then substitute it back into the equation

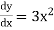
S =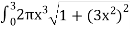

S =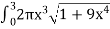

Using u-substitution and setting u= 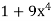and du=36x3dx,

We calculate

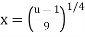
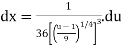
Plugging these values back into the integral we get,

S=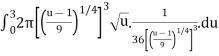

S =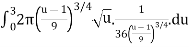

S =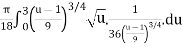

S =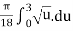

By integration we get

S =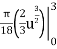

S =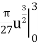

We will insert back for u, and we have u = 1+9x4, and then evaluate over the interval

S =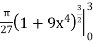

=

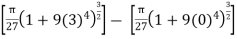
S = 2, 294.8 square units.

THEREFORE,

The surface area obtained by rotating y= x3 around the x-axis over the interval 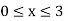is S = 2, 294.8

Q2) Find the volume generated by revolving the region bounded by y = x2 and the x-axis on [-2,3] about the x-axis.

A2) The volume(v) of the solid is

V =

=

=

=

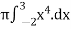
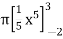
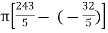
V = 55.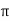

Q3) Solve the following improper Integral 

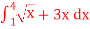
A3)

Given,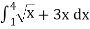

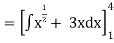
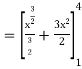
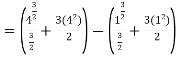
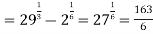
Q4) Solve the following improper Integral

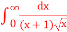
A4) Given,

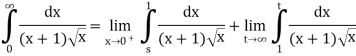
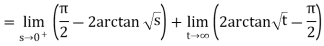
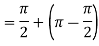
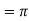
Q5) Solve the following improper Integral

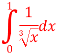
A5) Given

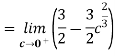
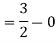
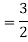
Q6) Solve the following improper Integral

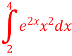
A6) Given

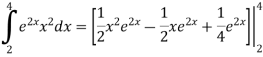
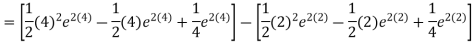
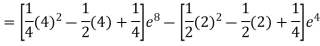
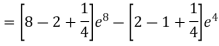
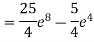
Q7) f(B) = 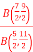     Solve the given function.

 A7)     =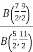 

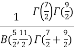
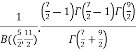=             [Recursive function for the gamma function]

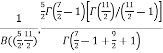=       [Recursive formula for the gamma function]

=

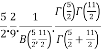
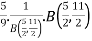=     [By the definition of Beta function]

=

Q8) B  =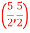

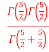
A8) = 

=

=

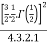
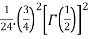
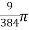= [because ]

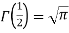Q9) Find the area of the surface generated by rotating the function about the x-axis over

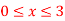  and the curve

A9) we have the equation of the form y=f(x) and we are rotating around the x-axis, we’ll use the formula

S =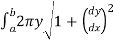

We will calculate 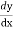and then substitute it back into the equation

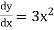
S =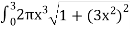

S =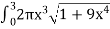

Using u-substitution and setting u= 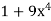and du=36x3dx,

We calculate

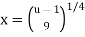
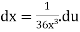
Plugging these values back into the integral we get,

S=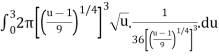

S =

S =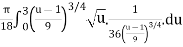

S =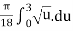

By integration we get

S =

S =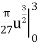

We will insert back for u, and we have u = 1+9x4, and then evaluate over the interval

S =

=

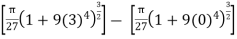
S = 2, 294.8 square units.

Therefore,

The surface area obtained by rotating y= x3 around the x-axis over the interval is S = 2, 294.8

Q10) Find the volume generated by revolving the region bounded by y = x2 and the x-axis on [-2,3] about the x-axis

A10) The volume(v) of the solid is

V =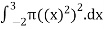

=

=

=

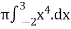
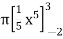
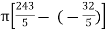
V = 55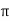.