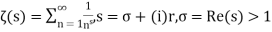Unit – 1C
Series
Q1) 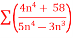 n
n
A1) L= 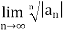 =
= 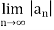 1/n
1/n
L= 
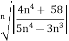 n =
n =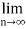
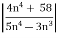
=  <1
<1
Hence the series converges.
Q2) Find the Taylor series for the following:
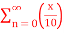
 =
= 
 <1
<1
A2)
 (x/10) <1 and (x/10) > -1
(x/10) <1 and (x/10) > -1
Therefore, radius of convergence is (-10,10)
 ROC =10
ROC =10
Q3) (a): f(n)5 = 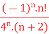 (b): f(x)=
(b): f(x)=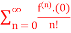
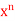
A3)
(a): f(n)5 = 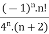
Here the ROC 4
(b): f(x)=
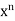
= f (0) +f’ (0)x +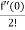 x2 +
x2 +  x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 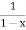
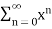
Q4) 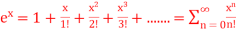
A4) Given
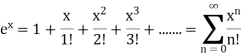
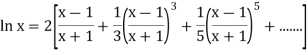
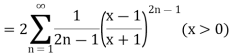
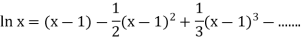
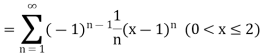
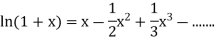
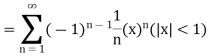
Q5) Leonhard Euler, the great Swiss mathematician introduced and named the number e in his calculus text in 1748.
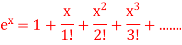
A5) Given
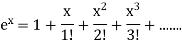
Putting x=1 in there, we get:
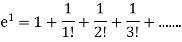
Which gives
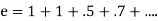
So, e is approximately 2.67 or 2<e<3 and the value of 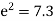 by using exp. Series
by using exp. Series
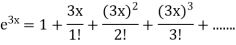
Which simplifies to:
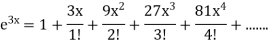
To write 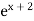 as a series, it is best to rewrite
as a series, it is best to rewrite 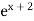 as
as 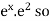 :
:


By adding & subtracting above two series, we get
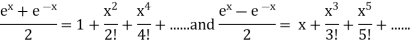

Q6) Find the Fourier series of f(x) = x in the interval 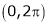
A6) Here 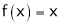 ;
; 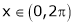
 Its Fourier series is given by
Its Fourier series is given by
 … (1)
… (1)
Where
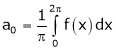
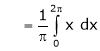
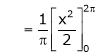
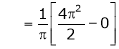
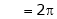
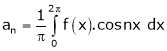
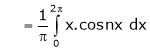
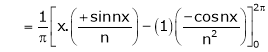

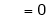
&
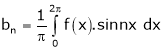
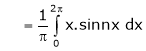
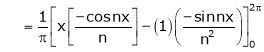
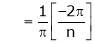
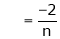
Hence the required Fourier series is
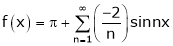
Q7) Find a Fourier series expansion in the interval 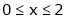 for
for
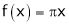 ;
; 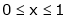
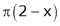 ;
; 
A7) Here
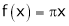 ;
; 
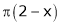 ;
; 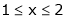
Hence, its Fourier series expansion is,
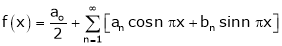 … (1)
… (1)
Where
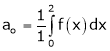
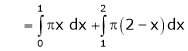
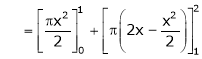
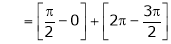


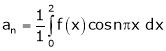
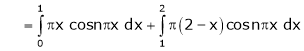
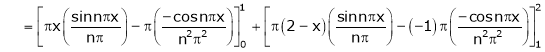
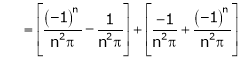

And
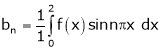
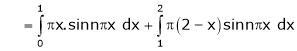

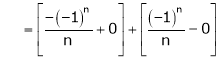
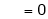
Hence equation (1) becomes
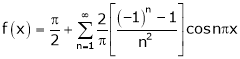
Q8) Find a Fourier series for
 ;
; 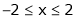
A8)
Here
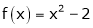 ;
; 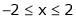
Since f(x) is even function hence 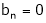
 It’s Fourier series is
It’s Fourier series is
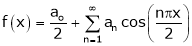 … (1)
… (1)
Where
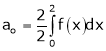
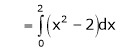
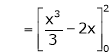
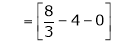
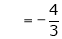
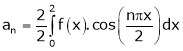
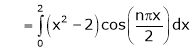
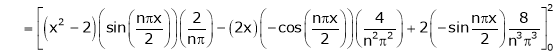
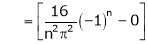
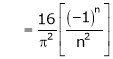
Hence equation (1) becomes,
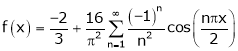
Q9) Find half range cosine series of 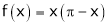 in the interval
in the interval 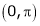 and hence deduce that
and hence deduce that
a) 
b) 
A9)
Here
 ;
; 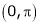
Hence it’s half range cosine series is,
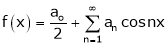 … (1)
… (1)
Where
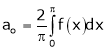
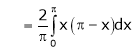


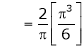
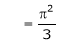
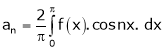
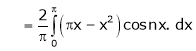
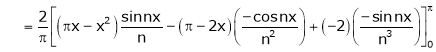
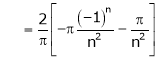

Hence equation (1) becomes,
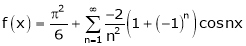
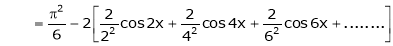
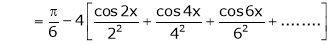 … (2)
… (2)
Put x = 0, we get
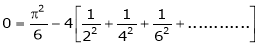
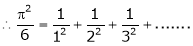
Hence the result
Put 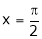 we get,
we get,
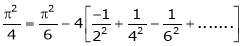
i.e. 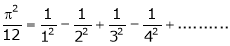
Q10) Using complex form, find the Fourier series of the function
f(x) = sinnx = 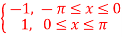
A10) We calculate the coefficients 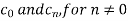
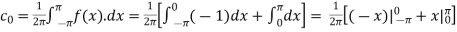
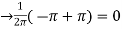
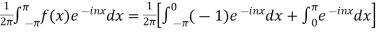
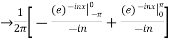 =
= 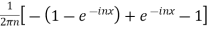
=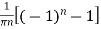
Hence the Fourier series of the function in complex form is

We can transform the series and write it in the real form by renaming as
n=2k-1,n=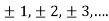
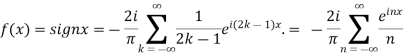
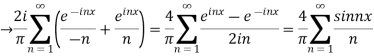
= 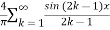
Q11) Using complex form find the Fourier series of the function f(x) = x2, defined on the interval [-1,1]
A11)
Here the half-period is L=1. Therefore, the co-efficient c0 is,
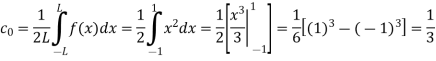
For n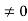

Integrating by parts twice, we obtain
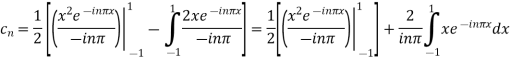
= 
= 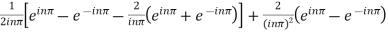
=  .
.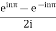
= 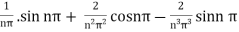 .
.
Q12) Consider 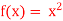 ,
, 
A12) The Fourier expansion is,
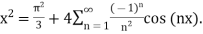
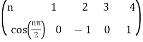
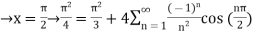
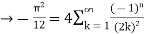
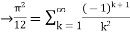
By Parseval’s formulae
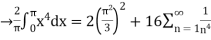
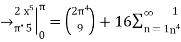
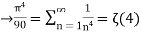
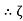 is Reiman Zeta function defined by:
is Reiman Zeta function defined by: