Unit - 2B
Matrices
Q1) Perform all the basic operations for the following matrices.
A = 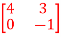 B =
B = 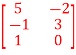 C =
C =  D =
D = 
A1) From the matrices we can know that b, d are compatible. This means we calculate B+D, B-D, D-B, but we cannot add or subtract any other pair of matrices.
The matrix cT = 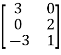 is a 3
is a 3  2 matrix, so we could add or subtract CT to from B and D
2 matrix, so we could add or subtract CT to from B and D
Addition and subtraction of matrices:
B + D = 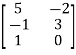 +
+ 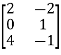 =
= 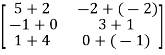 =
= 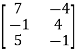
Similarly, we do subtraction as follow,
B – D = 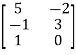 -
- 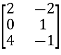 =
= 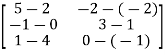 =
= 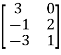
We do scalar multiplication for the above matrices.
-3A = 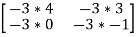 =
= 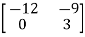
4C = 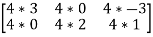 =
= 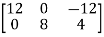
Q2) Find the scalar multiplication for the following:
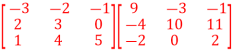
A2)
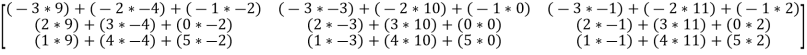
= 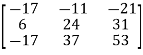
Q3) Solve the equations
4x+7y-9=0
5x-8y+15=0
A3) Given equation can be written in matrix form as A = 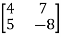 , X=
, X=  ,
,
B = 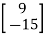
Given system can be written as: AX=B, where x= A-1 B
Let us find determinant :|A| = 4*(-8)-(5*7) = -32-35 = -67 So, solution exist.
Minor and co-factor of matrix A are:
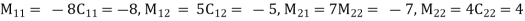
Cofactor matrix = 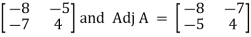
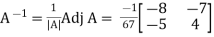
X = 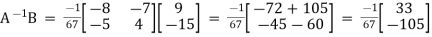
X = 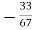 and Y =
and Y = 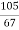
Q4) Solve the system of equations:
2x+y+3z = 1, x+z =2, 2x+y+z= 3
A4) Given equation can be written in matrix form as A = 
X = 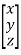 , B =
, B = 
Given system of equations can be written as AX = B where X = A-1B
Let us find determinant :|A| = 2(0-1)-1(1-2) +3(1-0) = -2+1+3 = 2.
So, solution exist.
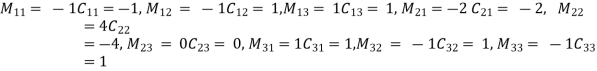
Cofactor = 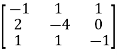 and Adj(A) =
and Adj(A) = 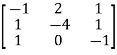
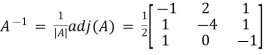
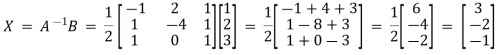
X = 3, Y = -2, Z = -1.
Q5) Reduce the following matrix into normal form and find its rank,

A5) Let A = 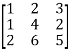
Apply  we get
we get
A 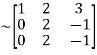
Apply 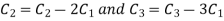 we get
we get
A 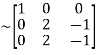
Apply 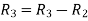
A 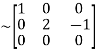
Apply 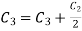
A 
Apply 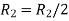
A 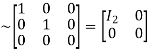
Hence the rank of matrix A is 2 i.e. 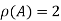 .
.
Q6) Reduce the following matrix into normal form and find its rank,

A6) Let A = 
Apply 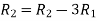 and
and 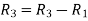
A
Apply 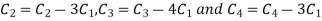
A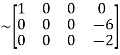
Apply 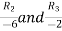
A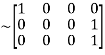
Apply 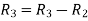
A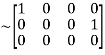
Apply 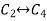
A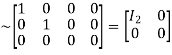
Hence the rank of the matrix A is 2 i.e. 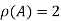 .
.
Q7) Reduce the following matrix into normal form and find its rank,

A7) Let A = 
Apply 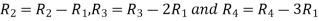
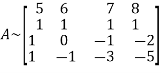
Apply 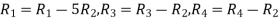
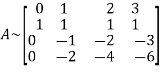
Apply 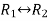
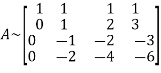
Apply 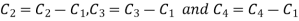
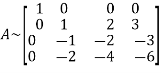
Apply 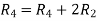 and
and 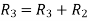

Apply 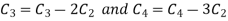
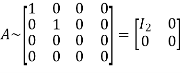
Hence the rank of matrix A is 2 i.e. 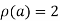 .
.
Q8) Determinants of a  Matrix
Matrix
If A = 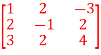 find |A|
find |A|
A8) 1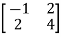 -2
-2 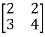 + (-3)
+ (-3) 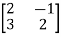
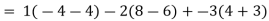
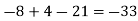
Therefore, determinant value = -33
Q9) Find the determinants of the following matrix.
A = 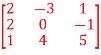
A9) 2*det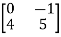 -(-3)
-(-3)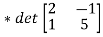 + 1*det
+ 1*det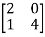
= 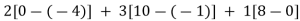
= 2(0+4)+3(10+1)+1(8)
= 8+3(11)+8
= 49.
Q10) Use Cramer’s rule to solve each system of equations.
2x+y = 10…. (1)
3x-2y = 8…. (2)
A10) we rewrite the given system of equations in the matrix form.
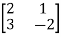 D=
D= 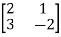 = 2(-2)-1(3) = -7
= 2(-2)-1(3) = -7
D  0, so the system is consistent.
0, so the system is consistent.
Now we solve for each variable by replacing the co-efficients of thet variable with the constants as shown below.
X = 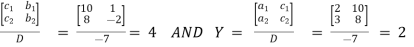
Therefore, the solution is (4, 2).
Q11) Use Cramer’s rule to solve each system of equations.
3x - 2y = -5 …. (1)
9x-6y = -15 …. (2)
A11) we rewrite the given system of equations in the matrix form.
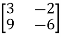 D=
D= 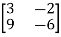 = 3(-6)-9(-2) = 0
= 3(-6)-9(-2) = 0
D = 0, so the system is either inconsistent or dependent.
Checking the numerators for X and Y to see if either is 0.
Now we solve for each variable by replacing the co-efficients of the variable with the constants as shown below.
X = 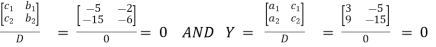
Since at least one numerator is 0, the system is dependent and has infinitely many solutions.
 Q12) Given 3
Q12) Given 3 3 Rectangular Matrix
3 Rectangular Matrix

A12) The augumented matrix is as follows




After applying the Gauss-Jordan elimination method:
The inverse of a matrix is as follows,


Q13) Find the inverse of
 A=
A= 
A13)

 Step 1: Adjoin the identity matrix to the right side of A:
Step 1: Adjoin the identity matrix to the right side of A:


Step 2: Apply row operations to this matrix until the left side is reduced to I. The computations are:



 R2
R2 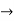 R2-R1 , R3
R2-R1 , R3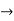 R3-R1
R3-R1


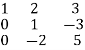
 R3
R3 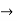 R3 + 2R2
R3 + 2R2


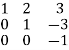
 R1
R1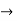 R1 -3R3 , R2
R1 -3R3 , R2 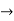 R2+3R3
R2+3R3



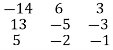 R1
R1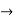 R1-2R2
R1-2R2

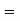
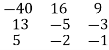
 Step 3: Conclusion: The inverse matrix is:
Step 3: Conclusion: The inverse matrix is:
A-1 = 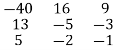
Q14) Find the inverse of matrix A given below:
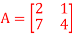
A14) Let A = IA
Or
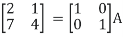
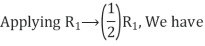
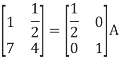
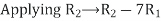
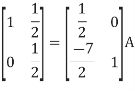
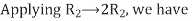
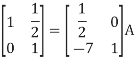
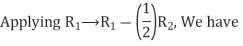
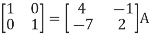
Thus, the inverse of matrix A is given by I =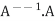
Therefore,
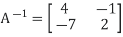
Q15) x+y+z=5
2+3y=5z=8
4x+5z=2

 A15) So for the given above set of linear equations the Guass-jordan method represents as the following
A15) So for the given above set of linear equations the Guass-jordan method represents as the following
1 1 1 5
2 3 5 8
4 0 5 2
 The augmented matrix is.,
The augmented matrix is.,
1 1 1
2 3 5
4 0 5
 Now we reduce the above matrix in gauss Jordan form.
Now we reduce the above matrix in gauss Jordan form.
 2 3 5 r2 r1
2 3 5 r2 r1
 1 1 1 r1 r2
1 1 1 r1 r2
4 0 5

1 2 4 r2 - 2r1
1 1 1
4 0 5
 1 2 4
1 2 4
1 1 1 r3 – r1
3 -2 1
So here represents the gauss Jordan method by having a unique number one diagonally in the matrix.
Q16) x+y+z=3
2x+3y=7z=0
X+3y-2z=17

 A16) The given set of linear equations can be written as.,
A16) The given set of linear equations can be written as.,
1 1 1 3
2 3 7 0
1 3 -2 17
The augmented matrix o
 For the given system of equations is.,
For the given system of equations is.,
1 1 1
2 3 7
1 3 -2

 1 1 1
1 1 1
7 3 2 c1 c2
-2 3 1

1 1 1
 5 1 0 r2 r2 - 2r1
5 1 0 r2 r2 - 2r1
-2 3 1
So, here the Guass-jordan method completes by making all the diagonal elements to unit number.
Q17) 2X+Y=4
X-3Y=9
X+4Y=-5
 A17) The augmented matrix is.,
A17) The augmented matrix is.,
2 1 4

 1 -3 9 r1 r2
1 -3 9 r1 r2
1 4 -5
 1 -3 9
1 -3 9
2 1 4 -2r1+r2 & -r1+r3
1 4 -5

1 -3 9
0 7 -14 ( 1/7) r2 &( 1/7) r3
0 7 -14

1 -3 9
0 1 -2 -1r2+r3
0 1 -2
1 0 3
0 1 -2
0 0 0
Here the final matrix we have reduced to echelon form and it also represents system of equations with x=3, y=-2.