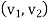Unit – 2D
Vector Spaces
Q1) Find the eigenvalues for the following matrix?
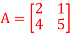
A1) Given
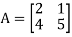
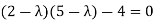
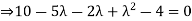
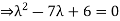
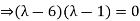
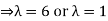
Hence the required eigenvalues are 6 and 1
Q2) Find the eigenvalues of a 
A2) Let A=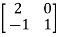 
Then,
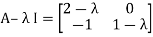
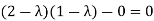
These are required eigenvalues.
Q3) Let us test whether the given matrices are symmetric or not i.e., we check for,
A = 
A =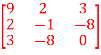 
A3) Now
=
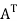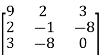
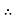A = 
Hence the given matric symmetric
Q4) Let A be a real symmetric matrix whose diagonal entries are all positive real numbers.
Is this true for all of the diagonal entries of the inverse matrix A-1 are also positive? If so, prove it. Otherwise give a counter example
A4) The statement is false, hence we give a counter example
Let us consider the following 2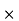
2 matrix
A =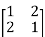 
The matrix A satisfies the required conditions, that is A is symmetric and its diagonal entries are positive.
The determinant det(A) = (1)(1)-(2)(2) = -3 and the inverse of A is given by
A-1=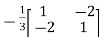 
= 
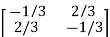
By the formula for the inverse matrix for 2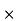
2 matrices.
This shows that the diagonal entries of the inverse matric A-1 are negative.
Q5) Let A and B be n
n skew-matrices. Namely AT = -A and BT = -B
(a) Prove that A+B is skew-symmetric.
(b) Prove that cA is skew-symmetric for any scalar c.
(c) Let P be an m
n matrix. Prove that PTAP is skew-symmetric.
A5) (a) (A+B)T = AT + BT = (-A) +(-B) = -(A+B)
Hence A+B is skew symmetric.
(b) (cA)T = c.AT =c(-A) = -cA
Thus, cA is skew-symmetric.
(c)Let P be an m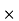
n matrix. Prove that PT AP is skew-symmetric.
Using the properties, we get,
(PT AP)T = PTAT(PT)T = PTATp
= PT (-A) P = - (PT AP)
Thus (PT AP) is skew-symmetric.
Orthogonal matrix: An orthogonal matrix is the real specialization of a unitary matrix, and thus always a normal matrix. Although we consider only real matrices here, the definition can be used for matrices with entries from any field.
Suppose A is a square matrix with real elements and of n x n order and AT is the transpose of A. Then according to the definition, if, AT = A-1 is satisfied, then,
A AT = I
Where ‘I’ is the identity matrix, A-1 is the inverse of matrix A, and ‘n’ denotes the number of rows and columns.
Q6) Prove Q= 
is an orthogonal matrix
A6) Given Q=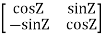 
So, QT =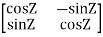 
…..(1)
Now, we have to prove QT = Q-1
Now we find Q-1
Q-1 =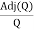 
Q-1 =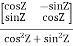 
Q-1 =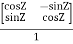 
Q-1 = 
… (2)
Now, compare (1) and (2) we get QT = Q-1
Therefore, Qis an orthogonal matrix.
Q7) Consider the vector space Pn of polynomials with inner product is
= 
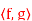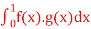and determine norm of the function f(x) = 5x2 +1.
A7) the norm of the function f generated by this inner product is,
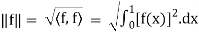
By using the above definition of norm, we get
= 
= 
= 
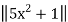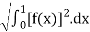
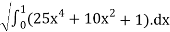
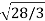
The norm of the function f(x) = 5x2 +1. Is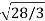 
Q8) Consider the vector space Pn of polynomials with inner product is
= 
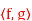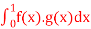
Determine the cosine of the angle between the functions f(x) = 5x2 and g(x) = 3x.
A8) we consider the standard form of the angle between two non-zero functions f and g is given by
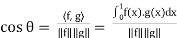
We first compute 
= 
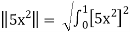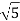and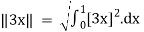 
= 
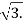
Thus,
= 
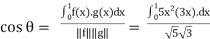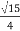
Q9) Let us consider the following 3 ×3 matrix
A = 
We want to diagonalize the matrix if possible.
A9) Step 1: Find the characteristic polynomial
The Characteristic polynomial p(t) of A is
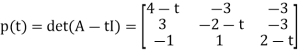
Using the cofactor expansion, we get
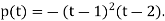
Step2: From the characteristic polynomial obtained step1, we see that eigenvalues are
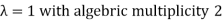
And 
Step2: Find the eigenspaces
Let us first find the eigenspaces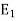 
corresponding to the eigenvalue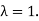 
By definition,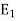 
is the null space of the matrix
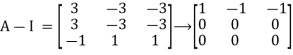
By elementary row operations.
Hence if (A-I) x=0 for x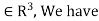
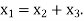
Therefore, we have
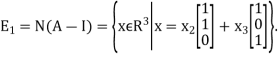
From this, we see that the set
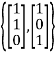
Is a basis for the eigenvalues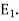 
Thus, the dimension of 
, which is the geometric multiplicity of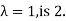
Similarly, we find a basis of the eigenspaces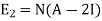 
for the eigenvalue 
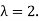We have
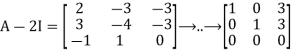
By elementary row operations.
Then if (A-2I) x=0 for x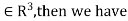
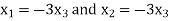
Therefore, we obtain
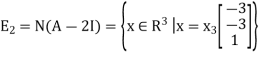
From this we see that the set
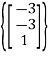
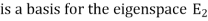and the geometric multiplicity is 1.
Since for both eigenvalues, the geometric multiplicity is equal to the algebraic multiplicity, the matrix A is not defective, and hence diagonalizable.
Step4: Determine linearly independent eigenvectors
From step3, the vectors
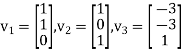
Are linearly independent eigenvectors.
Step5: Define the invertible matrix S
Define the matrix S=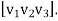
S=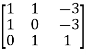
And the matrix S is non-singular (since the column vectors are linearly independent).
Step 6: Define the diagonal matrix D
Define the diagonal matrix
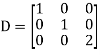
Note that (1,1) entry of D is 1 because the first column vector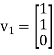 
Of S is in the eigenvalues 
that is 
is an eigenvector corresponding to eigenvalue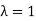 
Similarly, the (2,2) entry of D is 1 because the second column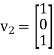 
of S is in 
.
The (3,3) entry of D is 2 because the third column vector 
of S is in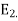 
(The order you arrange the vector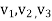 
to form S does not matter but once you made S, then the order of the diagonal entries is determined by S, that is , the order of eigenvectors on S)
Step7: Finish the diagonalization
Finally, we can diagonalize the matrix A as
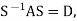
Where
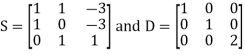
(Here you don’t have to find the inverse matrix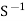 
unless you are asked to do so).
Q10) Consider the following set of vectors in R2
S =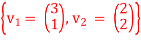 
use Gram-Schmidt, to obtain an orthogonal set of vectors.
A10) Performing Gram- Schmidt orthogonal process.
= 
- 
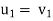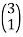
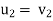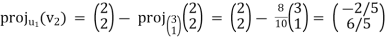
We check the vectors u1 and u2 are indeed orthogonal:
= 
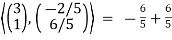= 0
We observe that the given vectors are orthogonal since the dot product is zero.
For non-zero vectors we can normalize the vectors by dividing out their sizes as shown above:
E1 =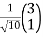 
E2 =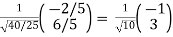 
Q11) Take v1 = (1,1,0) and v2 = (2,1,1) in R3, the list (v1, v2) is linearly independent. To illustrate the Gram-Schmidt procedure we proceed further.
A11) consider e1 =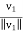 
= 
(1,1,0).
Now e2 =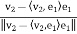 
The inner product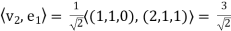 
S0,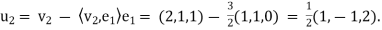 
Calculating the norm of u2, we obtain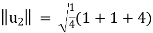 
= 
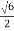
Hence normalizing this vector, we obtain.
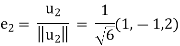
Therefore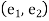 
are orthonormal and has the same span 
