Unit - 1
Vector Mechanics of Particles
Q1) What is Cartesian coordinate system?
A1) Assume a rectangular Cartesian coordinate system.
Let 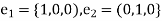 and
and 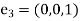 be orthogonal unit vectors of that system:
be orthogonal unit vectors of that system:
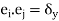 , (1)
, (1)
where 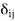 is the Kronecker delta symbol.
is the Kronecker delta symbol.
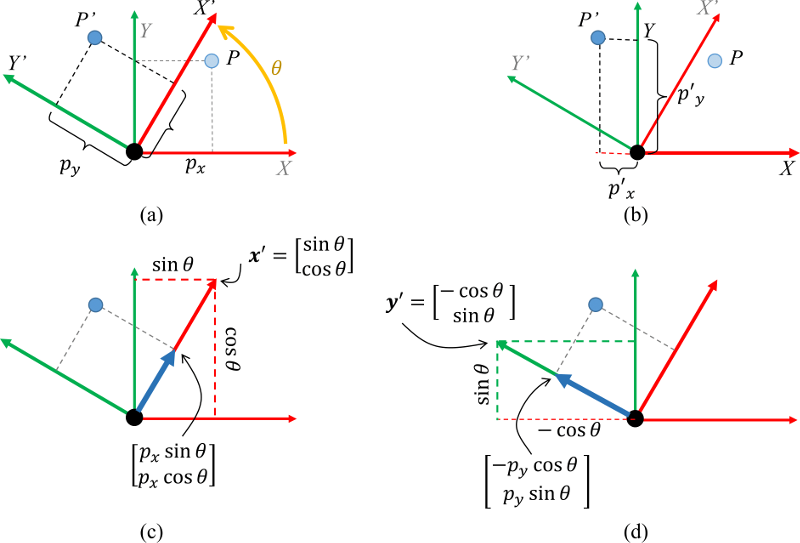
By rotation of the coordinate system, we achieve a new rectangular coordinate system.
Let  and
and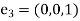 be orthogonal unit vectors of the new coordinate system
be orthogonal unit vectors of the new coordinate system 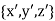 , that is,
, that is,
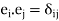 , (2)
, (2)
By the theorem of directional cosines, the coordinates of the vectors 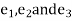 in the source of vectors
in the source of vectors 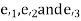 are the directional cosines. If we signify the directional cosines of the vector
are the directional cosines. If we signify the directional cosines of the vector 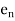 (with n = 1, 2, 3) through
(with n = 1, 2, 3) through 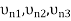 , respectively, then
, respectively, then
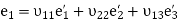
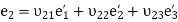
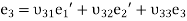
which can be written in a short form as
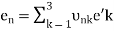 (n = 1, 2, 3). (3)
(n = 1, 2, 3). (3)
Equalities (1) and (2) imply
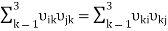 (i, j =1, 2, 3). (4)
(i, j =1, 2, 3). (4)
Rewrite equivalences (3) and (4) in the matrix form.
Let 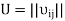 be the matrix of the directional cosines. Introduce also the column matrices
be the matrix of the directional cosines. Introduce also the column matrices 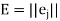 and
and 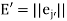 . Then
. Then
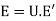 ,
,
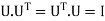 ,
,
where 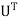 is the transfer of matrix U, and I is the identity matrix.
is the transfer of matrix U, and I is the identity matrix.
Note that the transfer of U is also the inverse of U. Then, we can easily find the formula of the inverse conversion (from the old basis to the new one):
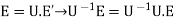
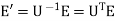
That is,
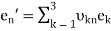 (n = 1, 2, 3).
(n = 1, 2, 3).
Now learning the transformation of the coordinates of an arbitrary vector a.
Some vector a can be stated as the linear grouping of basis vectors. If a1, a2 and a3 are the coordinates of a in the basis, and a'1, a'2 and a'3 are the coordinates of a in the new source then
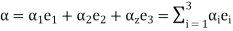 (5)
(5)
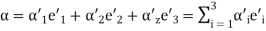 . (6)
. (6)
Thus,
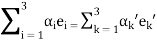 .
.
In view of equality (3) we obtain
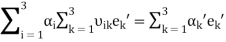
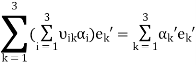
that yields the methods of transformation of the coordinates:
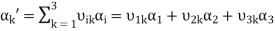 . (7)
. (7)
Similarly,
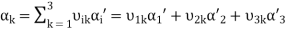 .
.
Till now we have interpreted the scalar product of vectors as a scalar quantity without a formal proof, seeing this proposition as the self-evident truth. A difficult explanation follows from the below theorem.
Q2) What are Polar coordinates?
A2) Cylindrical coordinates are a simple allowance of the two-dimensional polar coordinates to three dimensions. Recall that the position of a point in the plane can be described using polar coordinates (r,θ)(r,θ). The polar coordinate rr is the distance of the point from the origin. The polar coordinate θ is the angle between the xx-axis and the line segment from the origin to the point. Polar coordinates are showed in the below figure
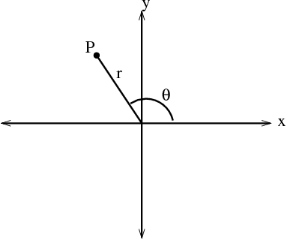
The cylindrical coordinates simply combine the polar coordinates in the xxy plane with the usual zz coordinates of the Cartesian coordinates. To form the cylindrical coordinates of a point PP, it is sufficient to project it to a point QQ in the xxy plane (see the following figure). So, take the polar coordinates (r, θ) (r, θ) of the point QQ, that is, rr is the distance from the origin to QQ and θθ is the angle between the positive xx axis and the line segment from the origin to QQ. The third cylindrical coordinate is equal to the usual zz coordinate. It is the distance of the signed point PP with respect to the xxy plane (being negative, it is PP is below the xxy plane). The following figure shows the cylindrical coordinates (r, θ, z) (r, θ, z) of the point PP.
You can further explore the properties of cylinder coordinates with the following applet. You can see how changing the coordinates (r, θ, z) (r, θ, z) changes the position of the PP point. As with the polar coordinates, we generally limit 0≤θ<2π0≤θ<2π and r≥0r≥0 to reduce the non-uniqueness of the cylinder coordinates. However, when r = 0r = 0, there is a non-uniqueness since the point PP is on the zz axis when r = 0r = 0, regardless of the value of θθ.
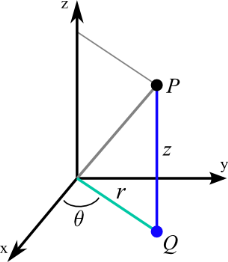
Cylindrical coordinates. Given the values for the cylindrical coordinates rr, θθ, and zz, the large blue dot shows the corresponding position in the Cartesian coordinates. You can edit rr, θθ and zz using the cursors or dragging the other displayed dots. The red dot is the projection of the large blue dot on the xxy plane. This projection offers perspective and helps visualize θθ and rr. The rr coordinate is the length of the red line segment from the origin to the red point. The coordinate coordinate is the angle formed by the red line segment with the positive xx axis; is the angle of the green portion of the disk portion in the xxy plane. The zz coordinate is equal to the zz coordinate of the Cartesian coordinates; is the height of the purple point on the zz axis.
Q3) What do you mean by Potential energy function?
A3) If a force acting on an object is only a function of position, it is said to be a conservative force and can be represented by a potential energy function that satisfies the derived condition for a one-dimensional case
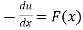 conceptual comments example
conceptual comments example
The integral form of this relationship is
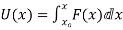 Example
Example
which can be taken as a definition of potential energy. Note that there is an arbitrary integration constant in that definition, demonstrating that any constant can be added to potential energy. In practice, this means that zero potential energy can be set at any convenient point.
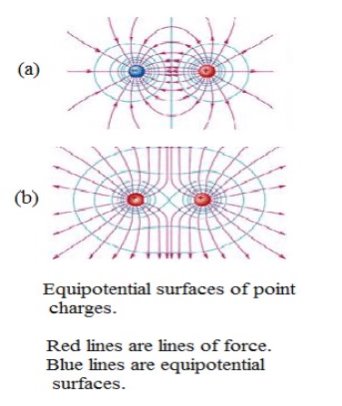
Equipotential surfaces. An equipotential surface is a surface at all points where the potential has the same value. Figure 3 shows sections of the equipotential surfaces associated with two different charges and two similar charges.
Since the potential energy of a charged body is the same at all points on a particular equipotential surface, it follows that no work is done to move a charged body on such a surface. Consequently, the equipotential surface passing through any point must be at right angles to the direction of the electric field at that point. Otherwise, the field would have a component on the surface and you would have to work against the field to move a charge in the direction of this component. Therefore, the lines of force and the equipotential surfaces form a mutually perpendicular network. In a charged conductor in which the charges are at rest (electrostatic situation), the lines of force on the surface are perpendicular to the surface. Then, the surface of said conductor is an equipotential surface. Furthermore, since the field inside a charged conductor is zero, the entire interior of the conductor is an equipotential volume, with the same potential as the surface.
Q4) What is Kepler problem?
A4) The movement of the sun and the earth is an example of a two-body problem ''. This is a relatively simple problem that can be solved analytically (it is interesting to note here, however, that adding a new object to the problem, for example the moon, makes it completely intractable. This is the famous three-body problem. ''). We can assume that, with a good approximation, the sun is stationary and is a convenient origin of our coordinate system. This is equivalent to moving to a center of mass '' coordinate system, where most of the mass is concentrated in the sun. The problem can be reduced to an equivalent body problem involving a reduced object mass given by
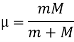
Meanwhile the mass of the earth is 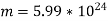 kg and the mass of the sun is
kg and the mass of the sun is 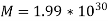 kg we find that for most practical purposes, the compact mass of the earth-sun system is that of the earth.
kg we find that for most practical purposes, the compact mass of the earth-sun system is that of the earth.
Henceforth, in the succeeding we are successful to consider the problem of a single particle of mass 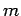 moving about a immovable center of force, which we take as the origin of the coordinate coordination. The gravitational force on the particle m is given by
moving about a immovable center of force, which we take as the origin of the coordinate coordination. The gravitational force on the particle m is given by
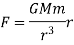
where the vector r is directed from M to m, and G is the gravitation constant
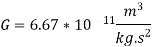
The negative sign suggests that the gravitational force is attractive and decreases with the separation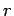 . The gravitational force is a central force'': its magnitude depends on the separation between the particles and its way is along the line that joins them. The statement is that the motion is confined to the xy plane. The angular momentum L lies on the third direction z and is a constant of motion, i.e. it is conserved:
. The gravitational force is a central force'': its magnitude depends on the separation between the particles and its way is along the line that joins them. The statement is that the motion is confined to the xy plane. The angular momentum L lies on the third direction z and is a constant of motion, i.e. it is conserved:
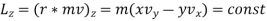
An added constant of motion in the total energy E given by
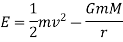
If we answer the coordinate system in the sum, the equation of motion is
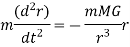
For computational purposes it is suitable to write it down in cartesian components:
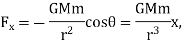
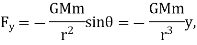
Hence, the calculations of motions in cartesian coordinates are:
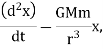
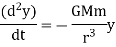
where 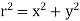 . These are coupled differential equations, meanwhile each differential equation comprises both
. These are coupled differential equations, meanwhile each differential equation comprises both  and y.
and y.
Q5) What Rotary coordinate system?
A5) The arithmetic for rotary coordinate systems can be quite complicated, however most physics can be understood in a relatively simple case. First, we will study the simple case, then we will expand the equations a little to include the general case.
Meanwhile any rotation is just a rotation in a plane, the simple case comprises the most overall rotation. Our simplification is that we will insert two coordinate axes in the plane of rotation. Since we have the choice of coordinate systems to solve our physics problems, this covers many cases. But sometimes, like motion on the earth's surface, we want to define our coordinates differently, and we'll cover that in the next section. In all cases, we will set our coordinates to match the origin of the inertial coordinate system and the rotary coordinate system.
Imagine investigating on a rotary table (rotation in the plane of the table). It is rotating around a definite point and we will call the point the origin of our coordinate systems. We know about the effective'' centrifugal force 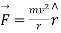 from Freshman Physics. If the table is revolving with constant angular frequency , we require
from Freshman Physics. If the table is revolving with constant angular frequency , we require 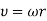 .
.
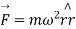
There is extra effective force that be determined by on velocity called the Coriolis Force. Lets recognize this just by supposing our rotating table is a frictionless air table. For our first experiment we will send a puck straight across the table through the origin. The puck energies from radius 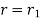 to radius r=0 and back to radius r1 in our experiment and we give the puck precisely the right velocity so that it marks this trip while the table experiences precisely one-half turn.
to radius r=0 and back to radius r1 in our experiment and we give the puck precisely the right velocity so that it marks this trip while the table experiences precisely one-half turn.
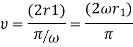
So far, we are talking about the motion detected from a non-rotating frame with the same origin.
The puck transfers in a straight line at constant velocity from one side of the table to the new as shown in the figure below.
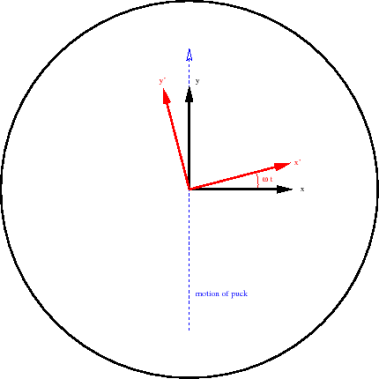
Now let’s see what occurs using the rotating coordinate system. The figure below gives a rough picture of the puck's path in the rotating coordinate system. It does not move in a straight line.
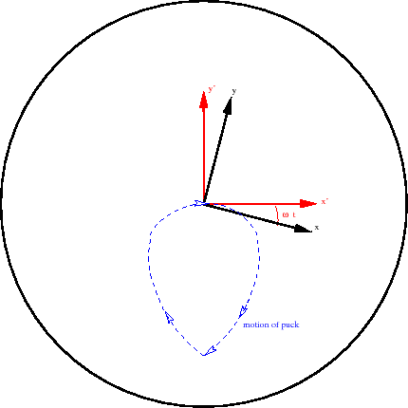
The disc appears with an internal radial velocity as before but also has a huge tangential component. The tangential component decreases as the disk approaches the origin. Cross the origin, then return to radius r1 on a path symmetrical with that of the origin. (Return to the same point due to the speed we chose for this experiment.)
In the rotating frame, there was clearly an effective force that was not radially outward. That was the Coriolis force.
Acceleration of a particle in a mobile frame of reference
The XYZ system shown in Figure 1 is an inertial frame of reference, while the X'Y'Z 'frame is a mobile (translation + rotation) frame of reference. The position of point P in the figure can be stated in terms of these two frames of reference:

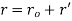
Where ro = the position of the origin of the revolving frame, and r' = the position of P comparative to the origin of the moving frame.
From above equation of Rotating Reference Frame, the displacement of point P can then be expressed as
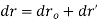
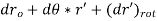
where dro = the displacement due to conversion of the origin of the rotating frame, dr' = the displacement of point P relation to the origin of the rotating frame, d x r' = the displacement due to rotation of the moving frame, and (dr')rot, the displacement of point P detected in the rotating frame (or the displacement of P relative to the moving frame).
From above equation the velocity of point P can be expressed as
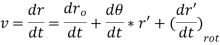
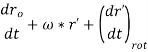
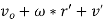
Where, v'r = the velocity of point P comparative to the moving reference frame.
Therefore, the velocity of point P comparative to the origin of the moving reference frame can be divided into the velocity due to rotation of the frame and the velocity detected in the rotating frame.
Acceleration of point P can then be found likewise:
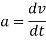
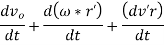
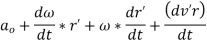
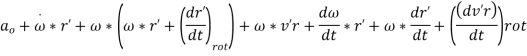
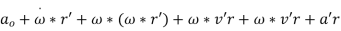
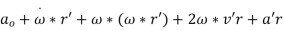
Where, a is the acceleration of point P, ao is the acceleration of the origin of the moving frame, and a'r is the acceleration of point P relative to the moving frame.
Q6) What is Centripetal Acceleration?
A6) Above term are the results of the translational and rotational acceleration of the moving reference frame, respectively. The 3rd term, x (x r'), is due to the rotation of the moving frame and, as shown in Figure 2, this vector heads toward the center of rotation (point C). This acceleration is named the centripetal acceleration. The above term is due to the motion of the point within the moving frame and is called the Coriolis acceleration. The previous term is due to the acceleration of the point inside the moving reference frame.

If the moving frame does not interpret but rotates with a constant angular velocity and point P does not move inside the moving frame, [4] can be basic to
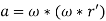 [5]
[5]
Meanwhile
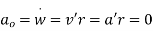 [6]
[6]
In order words, the centripetal acceleration is the basic must for a constant circular motion of a body around an axis of rotation. According to Newton's 2nd Law of Motion the force acting on a particle is equivalent to the its mass times acceleration. Therefore, from [6]:
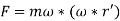 [7]
[7]
This force is the centripetal force which causes a constant circular motion of a body. Note that this force acts in the direction of the centre of rotation, point C shown in Figure 2.
If the angular velocity of the rotating position frame is not constant, [4] decreases to
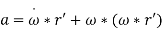 [8]
[8]
Meanwhile
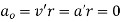 [9]
[9]
In the case of planar rotation where the direction of the angular velocity does not change, the 1st term of [8] can be labelled as the tangential acceleration since it is in the direction of x r' shown in Figure 2. (The angular velocity vector and the angular acceleration vector show the same direction in this case.) The 2nd term then converts the radial acceleration.
Q7) What is Quantum Harmonic Oscillator?
A7) A diatomic molecule vibrates somewhat like two masses on a spring with a potential energy that depends upon the square of the displacement from equilibrium. But the energy levels are quantized at equally spaced values.
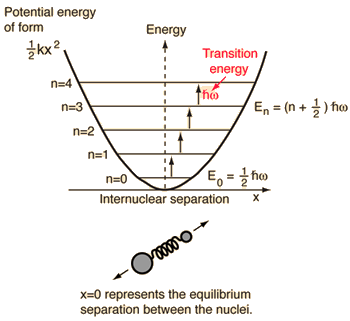
The energy levels of the quantum harmonic oscillator are
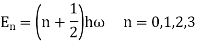
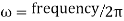
h=plank’s constant/2
and for a diatomic molecule the natural frequency is of the form
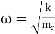 k=bond force constant
k=bond force constant
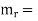 reduced mass
reduced mass
where the reduced mass is given by
This frequency shape is the same as the classical simple harmonic oscillator. The most notable difference for the quantum case is the so-called "zero-point vibration" of the ground state n = 0. This implies that the molecules are not completely at rest, even at absolute zero temperature.
The quantum harmonic oscillator has suggestions distant outside the simple diatomic molecule. It is the basis for understanding complex modes of vibration in larger molecules, the motion of atoms in a solid network, the theory of heat capacity, etc. In real systems, the energy distances are the same only for the lower levels where the potential is a good approximation of the harmonic "mass in a spring" potential. The harmonic terms that appear in the potential of a diatomic molecule are useful for mapping the detailed potential of such systems.
A large system moves slowly toward equilibrium. An undersized system moves rapidly toward equilibrium, but will oscillate around the equilibrium point when it does. A critically damped system moves as fast as possible towards equilibrium without oscillating around equilibrium.
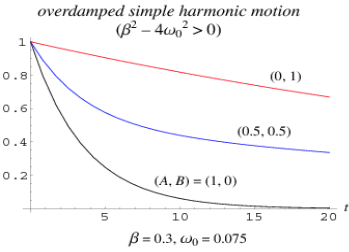
Oversized simple harmonic motion
Q8) What is Critically Damped Simple Harmonic Motion?
A8) Critically Damped Simple Harmonic Motion
Critical damping is a special case of damped simple harmonic motion
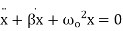 (1)
(1)
in which
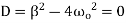 (2)
(2)
where 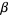 is the damping constant. Therefore
is the damping constant. Therefore
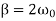 (3)
(3)
In this case, D=0 so the solutions of the form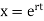 satisfy
satisfy
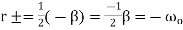 (4)
(4)
One of the solutions is therefore
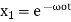 (5)
(5)
In order to find the other linearly independent solution, we can make use of the identity
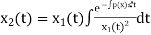 (6)
(6)
Since we have 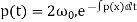 simplifies to
simplifies to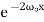 . Equation (6) therefore becomes
. Equation (6) therefore becomes
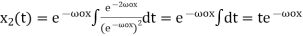 (7)
(7)
The general solution is therefore
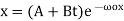 (8)
(8)
In terms of the constants A and B, the initial values are
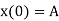 (9)
(9)
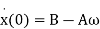 (10)
(10)
so
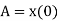 (11)
(11)
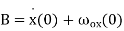 (12)
(12)
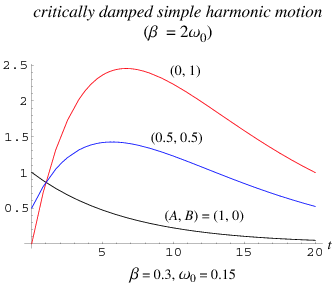
The above plot shows a critically damped simple harmonic oscillator with, 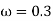 ,
,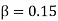 for a variety of initial conditions (A, B)
for a variety of initial conditions (A, B)
For sinusoidally forced simple harmonic motion with critical damping, the equation of motion is
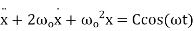 (13)
(13)
and the Wronskian is
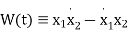 (14)
(14)
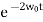 (15)
(15)
Plugging this into the equation for the particular solution gives
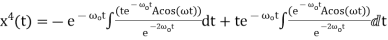 (16)
(16)
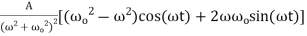 (17)
(17)
Applying the harmonic addition theorem then gives
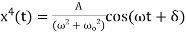 (18)
(18)
where
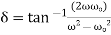 (19)
(19)
Q9) What is Damped Oscillations?
A9)
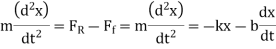
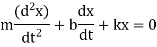
where b is the damping constant.
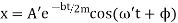
where 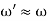 when the damping is small (small b).
when the damping is small (small b).
Announcement that this solution signifies oscillatory motion with exponentially reducing amplitude
Q10) What is Forced Oscillations and Resonance?
A10)
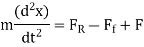
One common condition happens when the driving force itself oscillates, in which case we may write
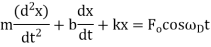
where 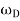 is the (angular) frequency of the driving force.
is the (angular) frequency of the driving force.
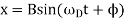
where the amplitude of these oscillations, B, depends on the parameters of the motion, 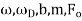
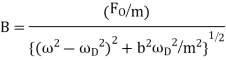
The amplitude, B, has a determined value when 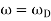 . This is called the resonance condition. Note that at resonance, B, can become very large if b is small. (In the diagram at right
. This is called the resonance condition. Note that at resonance, B, can become very large if b is small. (In the diagram at right 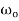 is the natural frequency of the oscillations,
is the natural frequency of the oscillations, 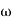 , in the above analysis). In designing physical systems, it is very important to find the system's natural frequencies of vibration and provide sufficient damping in case of resonance. This clearly did not occur in the design of the Tacoma Narrows Bridge (Tacoma Narrows Newsreel) in 1940.
, in the above analysis). In designing physical systems, it is very important to find the system's natural frequencies of vibration and provide sufficient damping in case of resonance. This clearly did not occur in the design of the Tacoma Narrows Bridge (Tacoma Narrows Newsreel) in 1940.
There are many physical and engineering systems where resonance is very important e.g., shock absorbers, earthquakes, loudspeakers, NMR, microwave ovens etc.