find(values, target)
{
for(i = 0; i<values.length; i++)
{
if (values[i] == target)
{ returni; }
}
return –1;
}
If element is found this function returns index of that element otherwise it returns –1.Example : we have an array of integers, like the following:Elements | 9 | 6 | 7 | 12 | 1 | 5 |
Index | 0 | 1 | 2 | 3 | 4 | 5 |
9 | 6 | 7 | 12 | 1 | 5 |
9 | 6 | 7 | 12 | 1 | 5 |
9 | 6 | 7 | 12 | 1 | 5 |
0 | 1 | 2 | 3 | 4 | 5 |
P1 : Program for Linear Search
#include<stdio.h>
#include<conio.h>
int search(int [],int, int);
void main()
{
int a[20],k,i,n,m;
clrscr();
printf(“\n\n ENTER THE SIZE OF ARRAY”);
scanf(“%d”,&n);
printf(“\n\nENTER THE ARRAY ELEMENTS\n\n”);
for(i=0;i<n;i++)
{
scanf(“%d”,&a[i]);
}
printf(“\n\nENTER THE ELEMENT FOR SEARCH\n”);
scanf(“%d”,&k);
m=search(a,n,k);
if(m==–1)
{
printf(“\n\nELEMENT IS NOT FOUND IN LIST”);
}
else
{
printf(“\n\nELEMENT IS FOUND AT LOCATION %d”,m);
}
}
getch();
}
int search(int a[],intn,int k)
{
inti;
for(i=0;i<n;i++)
{
if(a[i]==k)
{
return i;
}
}
if(i==n)
{
return –1;
}
}
if(key==A[mid])
return mid
Case 2 : If key is less than middle element then element is present in left half of array. Update High and goto step 2.if(key<A[mid])
High= Mid–1
goto step 2
Case 3 : If key is greater than middle element then element is present in right half of array. Update Low and goto step 2.if(key>A[mid])
Low= Mid+1
goto step 2
Case 4:if(Low>High)Print element not found.
Iterative algorithm for Binary Search
intBinarySearch( int A[],int x)
{
intmid,n;
int Low = 0;
int High = n–1;
while ( Low <= High )
{
mid = (Low + High) / 2;
if ( A[mid] == x )
return mid;
if ( A[mid] > x )
High = mid – 1;
else Low = mid + 1;
}
return –1;
}
Q2. Write a program for linear search.A2.P1 : Program for Linear Search
#include<stdio.h>
#include<conio.h>
int search(int [],int, int);
void main()
{
int a[20],k,i,n,m;
clrscr();
printf(“\n\n ENTER THE SIZE OF ARRAY”);
scanf(“%d”,&n);
printf(“\n\nENTER THE ARRAY ELEMENTS\n\n”);
for(i=0;i<n;i++)
{
scanf(“%d”,&a[i]);
}
printf(“\n\nENTER THE ELEMENT FOR SEARCH\n”);
scanf(“%d”,&k);
m=search(a,n,k);
if(m==–1)
{
printf(“\n\nELEMENT IS NOT FOUND IN LIST”);
}
else
{
printf(“\n\nELEMENT IS FOUND AT LOCATION %d”,m);
}
}
getch();
}
int search(int a[],intn,int k)
{
inti;
for(i=0;i<n;i++)
{
if(a[i]==k)
{
return i;
}
}
if(i==n)
{
return –1;
}
}
Program for Binary Search
#include<stdio.h>
#include<conio.h>
void main()
{
intn,i,search,f=0,low,high,mid,a[20];
clrscr();
printf("Enter the number of elements:");
scanf("%d",&n);
for(i=1;i<=n;i++)
{
printf("Enter the number in ascending order a[%d]=",i);
scanf("%d",&a[i]);
}
printf("Enter the element to be searched:");
scanf("%d",&search);
low=0;
high=n–1;
while(low<=high)
{
mid=(low+high)/2;
if(search<a[mid])
{
high=mid–1;
}
else if(search>a[mid])
{
low=mid+1;
}
else
{
f=1;
printf("Element is found at the position %d:",mid);
exit();
}
}
if(f==0)
{
printf("Element not found");
}
getch();
}
Write a Program for Bubble sort in C
#include <stdio.h>
#include<conio.h>
voidbubble_sort(int A[], int n);
int main()
{
int A[100], n, i, j, swap;
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter the elements\n", );
for (i = 0; i< n; i++)
scanf("%d", &A[i]);
bubble_sort(A, n);
printf("Sorted list in ascending order:\n");
for ( i = 0 ; i< n ; i++ )
printf("%ld\n", A[i]);
return 0;
}
voidbubble_sort(int A[], int n)
{
inti, j, t;
for (i = 0 ; i< ( n – 1 ); i++)
{
for (j = 0 ; j < (n – i – 1); j++)
{
if (A[j] > list[j+1])
{
/* Swapping */
t = A[j];
A[j] = A[j+1];
A[j+1] = t;
}
}
}
}
Complexity Bubble sort: Suppose we have a list with n elements, and each element perform n – 1 comparisons with elements to its left, and swap, if necessary. Best Case: If the list is already sorted, only one iteration is performed and complexity is O(1). Average and Worst case: For n elements at most n – 1 swap operations is performed in each pass. The worst and average case complexity is O(n2). Q6. Explain insertion sort?A6. Insertion Sort reads all elements from 1 to n and inserts each element at its proper position. This sorting method works well on small list of elements. Procedure for each pass is as follows.Pass 1 : A[l] by itself is trivially sorted.Pass 2 : A[2] is inserted either before or after A[l] so that: A[l], A[2] is sorted.Pass 3 : A[3] is inserted into its proper place so that: A[l], A[2], A[3] is sorted. Pass 4 : A[4] is inserted into its proper place A[l], A[2], A[3], A[4] is sorted.Pass N : A[N] is inserted into its proper place in so that: A[l], A[ 2 ] , . . . , A[ N ] is sorted Q7. Write a program on selection sort?A7.Program to perform Selection Sort.
#include <stdio.h>
int main()
{
int A[100], n, i, j, s, temp;
/* n=total no. of elements in array
s= smallest element in unsorted array
temp is used for swapping */
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter %d integers\n", n);
for ( i = 0 ; i< n ; i++ )
scanf("%d", &A[i]);
for ( i = 0 ; i< ( n – 1 ) ; i++ )
{
s = i;
for ( j = i + 1 ; j < n ; j++ )
{
if ( A[s] > A[j] )
s = j;
}
if ( s != i )
{
temp = A[i];
A[i] = A[s];
A[s] = temp;
}
}
printf("Sorted list in ascending order:\n");
for ( i = 0 ; i< n ; i++ )
printf("%d\n", A[i]);
return 0;
}
Output: Enter number of elements 5 Enter 5 integers 4 1 7 5 9 Sorted list in ascending order 1 4 5 7 9 Q8. Explain the complexity of selection sort?A8. In selection sort outer for loop is executed n–1 times. On the kth time through the outer loop, initially the sorted list holds k–1 elements and unsorted portion holds n–k+1 elements. In inner for loop 2 elements are compared each time. Thus, 2*(n–k) elements are examined by the inner loop during the k th pass through the outer loop. But k ranges from 1 to n–1. Total number of elements examined is: T(n) = 2*(n –1) + 2*(n–2) + 2*(n–3) + .. + 2*(n–(n–2)) + 2*(n–(n–1)) = 2*((n–1) + (n–2) + (n–3) + ... + 2 + 1) (or 2*(sum of first n–1 integers) = 2*((n–1)*n)/2) = n2 – n, so complexity of algorithm is O(n2). Q9. Write a program on insertion sort?A9.Program to implement insertion sort.
#include <stdio.h>
int main()
{
int n, A[100], i, j, t;
printf("Enter number of elements\n");
scanf("%d", &n);
printf("Enter %d integers\n", n);
for (i = 0; i< n; i++) {
scanf("%d", &A[i]);
}
for (i = 1 ; i<=( n – 1); i++)
{
j = i;
while ( j > 0 && A[j] < A[j–1])
{
t = A[j];
A[j] = A[j–1];
A[j–1] = t;
j––;
}
}
printf("Sorted list in ascending order:\n");
for (i = 0; i<= n – 1; i++) {
printf("%d\n", A[i]);
}
return 0;
}
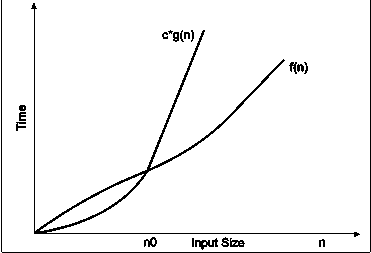
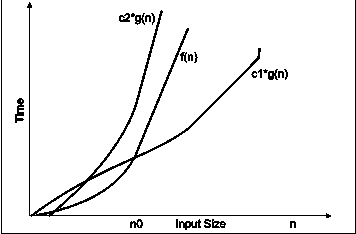
Output : Enter number of elements 5 Enter 5 integers 9 4 2 5 3 Sorted list in ascending order 2 3 4 5 9 Q10. Explain the complexity of insertion sort?A10. Worst Case Complexity: In the worst case, for each i we do (i – 1) swaps inside the inner for–loop–therefore, overall number of swaps (when i goes from 2 to n in the outer for loop) is T(n) = 1 + 2 + 3 +...+(I – 1) +....+ n – 1 = n (n – 1)/2 = O(n2) Average case Complexity is O(n2). Best Case Complexity is O(n). Q11. Write a program to find the roots of the equation?A11.Algorithm:Step 1: StartStep 2: Read a,b,cStep 3: Initialize d <- (b*b) – (4*a*c)Step 4: Initialize r<- b/2*aStep 5: if d>0 go to step 6Step 6: r1 = r+(sqrt(d)/2*a) and r2 = r-(sqrt(d)/2*a)Step 7: print roots are real and distinct first root r1, second root r2Step 8: if d=0 go to step 9else go to step 10Step 9: print roots are real and equal -rStep 10 : d= -dStep 11: im = sqrt(d)/2*aStep 12: print roots are imaginary, first root r+iim, second root r-iimStep 13: stop Program:void main(){float a,b,c,r,d,r1,r2,im;clrscr();printf(“\n\t Quadratic Eqution\n\n Enter the coefficients\n”);scanf(“%f%f%f”, &a,&b,&c);d= (b*b) –(4*a*c);r=b/2*aif(d>0){r 1 = -r + (sqrt (d)/2*a)r2 = -r - + (sqrt (d)/2*a)printf(“\n Roots are real and distinct \n\n first root\t: %.2f\n\n second root\t:%.2f \n”,r1,r2);}else if(d==0)printf(“\n Roots are real and equal \n\n roots =:%.2f,-r);}else{d=-d;im=sqrt(d)/2*a;printf(“\nRoots are imaginary \n\nfirst root\t;%.2f\n\nsecond root\t:%.2f-i%.2f”,r,im,r,im);}getch();}Q12. Explain the notion of order of complexity?A12. To express the running time complexity of algorithm three asymptotic notations are available. Asymptotic notations are also called as asymptotic bounds. Notations are used to relate the growth of complex function with the simple function. Asymptotic notations have domain of natural numbers. These notations are as follows1. Big-oh notation: Big-oh notations can be express by using ‘o’ symbol. This notation indicates the maximum number of steps required to solve the problem. This notation expresses the worst case growth of an algorithm. Consider the following diagram in which there are two functions f(x) and g(x). f(x) is more complex than the function g(x).
|
|
|
|
|
|