Unit - 7
Torsion
Q1) What is theory of torsion?
A1)
Q2) Derive the torsion equation?
A2) Consider a shaft of radius R and length L is subjected to torque T on the free end and other end is fixed.
Initially the line of the shaft is horizontal AB before twisting and after twisting it takes position AB’ as shown in fig.
Shear strain <BAB’ = 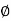 and Angle of twist <BOB’ =
and Angle of twist <BOB’ = 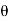
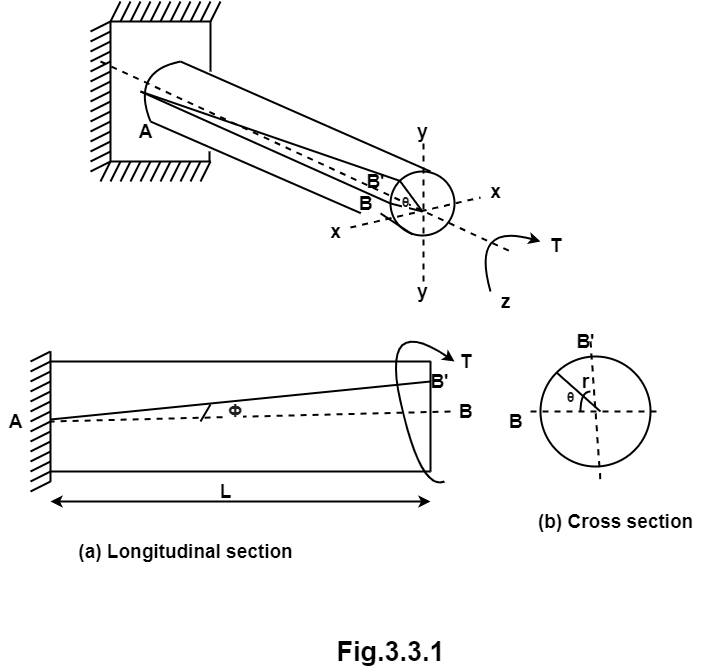
For longitudinal section,
tan  =
= 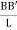 tan
tan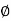 =
= 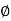
BB’=L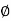 ………………...(i)
………………...(i)
From cross-section,
Length of arc = Radius 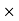 Angle tan
Angle tan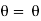
BB’=r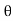 ……………. (ii)
……………. (ii)
From equation I and ii
L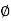 = r
= r
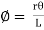 …………. (iii)
…………. (iii)
By definition shear modulus,
G=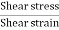 =
=
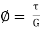 ……...(iv)
……...(iv)
Equation for (iii) and (iv),
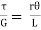
 =
= 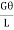 ……………. (v)
……………. (v)
Maximum shear stress occurs at radius R.
 =
= 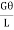
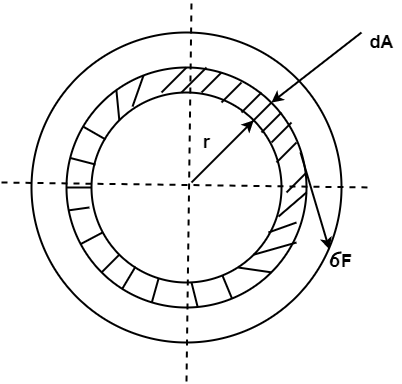
Now consider elemental ring of area dA at radius r from center O.
Shear force on elemental ring = Stress 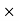 Area
Area
dF = 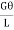
 dA
dA
Torsional moment on ring,
dT = dF  r =
r = 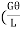
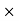 rdA)
rdA)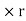
dT = 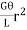 dA
dA
Now torsional moment on whole sectional,
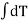 =
= 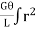 dA
dA
But we know, 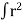 dA = polar moment of inertia = J
dA = polar moment of inertia = J
T = 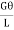
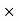 J
J
 =
=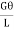 ……………...(vii)
……………...(vii)
From equation (vi) and (vii), we get,
 =
= 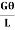 =
= 
Q3) What is assumptions of torsion?
A3)
Q4) A metal bar 15mm diameter subjected to pull of 40KN elongated by 0.5 mm over a gauge length of 500 mm. In a torsion test on the same material, maximum shear stress of 45Mpa was measured on a bar of 50mm diameter and an angle of twist over a length of 300 mm was measured 0.4 degree. Determine Poisson’s ratio for the material.
A4) Given:
Tensile test: D = 15mm P = 40KN
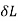 = 0.5 mm L = 500 mm
= 0.5 mm L = 500 mm
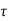 = 45Mpa D = 50 mm
= 45Mpa D = 50 mm
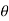 = 0.4
= 0.4 L = 300mm
L = 300mm
To find: 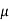
(i) Modulus of elasticity from tension test.
E = 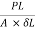 =
= 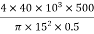 = 226.35
= 226.35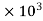 Mpa
Mpa
(ii) Shear modulus from torsion test:
G = 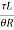 = 77.35
= 77.35 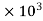 Mpa
Mpa
(iii) Possions ratio
E = 2G (1+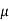 )
)
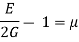

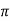 = 1.463-1 = 0.463
= 1.463-1 = 0.463
Q5) A hallow circular of 200 mm external diameter, thickness of metal 20mm is rotating at 180rpm. The angle of twist of 3m length was found to be 0.7 . Calculate the power transmitted and maximum shear stress induced in the material. Take G = 80
. Calculate the power transmitted and maximum shear stress induced in the material. Take G = 80 
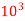 Mpa.
Mpa.
A5) Given
D = 200 mm
t = 20 mm
N = 180 rpm
L = 3m = 3000 mm
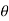 = 0.01222 radian
= 0.01222 radian
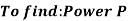
Internal diameter d= D – 2t = 200 - 2 20 = 160 mm
20 = 160 mm
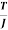 =
= 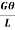
T = 30.2208 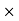
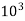 N.M
N.M
Power p = 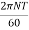 = 569.65 KW
= 569.65 KW
Q6) Define torsion rigidity?
A6) Torsion rigidity
Torsion rigidity K in the product of modulus of rigidity G and polar moment of inertia I. SI unit is N.m2
K= GK
Q7) What is combined torsion and bending of circular shafts?
A7) Cases stand up along with in propeller shafts of ships wherein a shaft is subjected to direct thrust similarly to bending second and torsion. In such instances the direct stresses because of bending second and the axial thrust should be combined right into a single resultant.
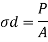
Where,
P= axial thrust
A= Area of cross section
2. Bending stress
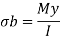
Where,
M= Bending moment
I = Moment of inertia
3. Torsion Stress
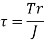
Where,
T= Torque
R= Radius of shaft
J= polar moment of inertia
Combined Stresses:
Under combination of these stresses,
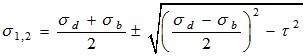
2. Maximum shear stress
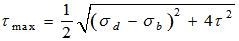
Equivalent Moment and Torque
Equivalent bending second can be defined because the bending second with the intention to produce the identical direct pressure as produced by the bending second and torque appearing separately. Similarly, the equivalent torque can be defined because the torque which will produce the identical most shear pressure as produced by the bending second and torque appearing separately.
For a circular shaft of diameter, d = 2r
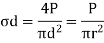
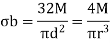
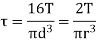
Power transmitted by a shaft
Torque= power (P) x 60 /2n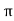
Where power is measured in watts and n is the speed in rpm
Q8) What are the Principal Stress and maximum Shear stresses under combined loading of bending and torsion?
A8) Consider a shaft subjected to the bending moment M and twisting moments T bending moment by using bending formula
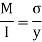
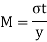
Bending stress
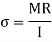
Twisting moment by torsion formula
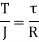
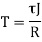
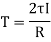
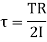
If 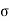 is the normal stress and
is the normal stress and 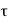 is the shear stress the principal stresses are given by
is the shear stress the principal stresses are given by
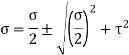
Substituting the value from equation
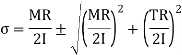
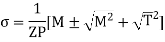
Where Zp is polar sectional modulus, Zp = 1/R
Equivalent bending moment
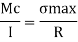
Q9) What do you mean by of close coiled helical springs?
A9) Closed Coiled Helical Springs: Designed to withstand stretching and twisting, these springs also are referred to as tension/extension springs.
These springs function a watch or a hook on the stop for attachment. These springs can undergo strain because of excessive torsion or bending
Spring is a vital element in nearly every machinery. These springs perform specific features in specific applications.
These take in shocks in vehicles jogging on choppy roads.
These shop power in toys and circuit breakers.
These deliver cushion impact in sofas and cars.
Springs are of various sorts particularly close and open coiled helical springs, laminated and spiral springs.
This spring is subjected to both axial load and axial couple.
The parameters to be studied in springs are stress, stiffness, deflection and resilience.