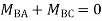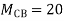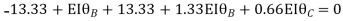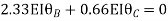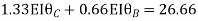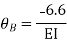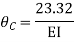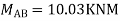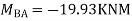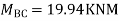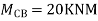Unit-2
Analysis of Beams and Frames
Q1) Explain the condition when fixed beam carrying udl throughout.
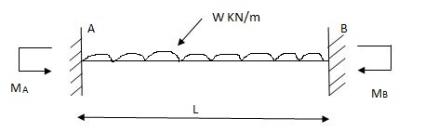
A1) Fixed beam carrying udl throughout:
Area & (A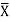 ) @B
) @B
For fig (i) ……………..
(-) 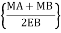 (L) …………..(i)
(L) …………..(i)
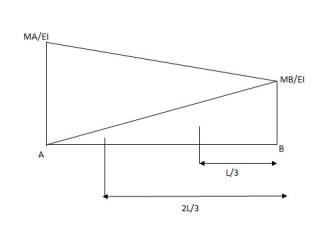
(A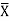 ) @B =
) @B = 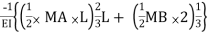
= (-) 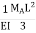 +
+ 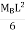
= (-)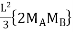 ……………. (II)
……………. (II)
Fig (2)
A =  (L)
(L) 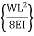 =
= 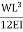
A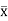 B =
B =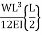 =
= 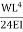
As per principle (1)
Total area =0
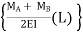 +
+ 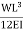 =0
=0
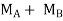 =
= 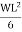 ……….(I)
……….(I)
As per principle (2)
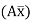 @B =0
@B =0
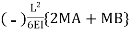 +
+ 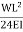 =0
=0
(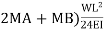 ……………. (2)
……………. (2)
From (1),
MB = 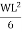 = MA put in (2)
= MA put in (2)
2MA + 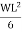 MA +
MA + 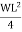
MA =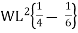
MA = 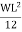
MB = 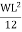
Fixed beam carrying udl end moments are 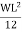
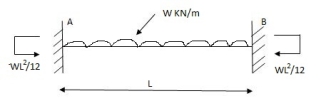
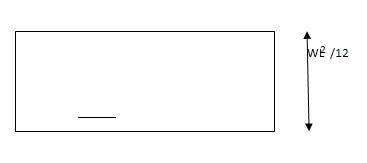
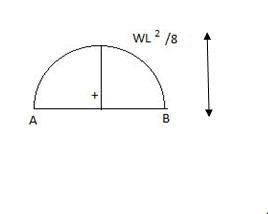
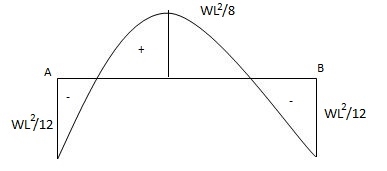
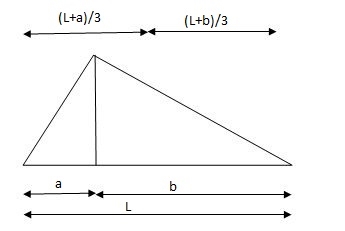
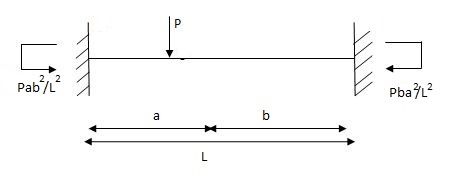
Q2) Explain the condition fixed beam with point load.
A2) Fixed beam with point load.
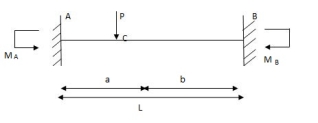
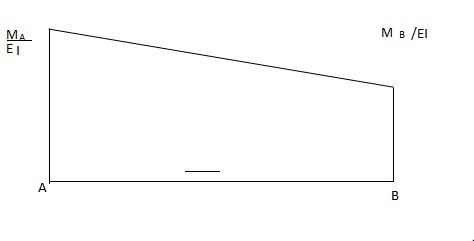
Area &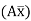 @B for free BMD
@B for free BMD
A =  (L)
(L) 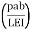
A =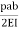
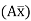 @B =
@B = 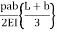 =
= 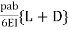
(2) As per principle (1)
Total Area =0
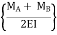 (L) +
(L) + 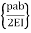 =0
=0
MA + MB = 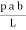 ……….. (1)
……….. (1)
As per principle (2)
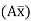 @B = 0
@B = 0
(-) 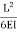 (2MA+2MB) +
(2MA+2MB) +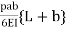 =0
=0
2MA+2MB =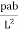 (L + b) ………… (2)
(L + b) ………… (2)
From (1)
MB = 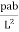 MA (Put in eqnc2)
MA (Put in eqnc2)
2MA + 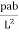 (L +b)
(L +b)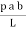
MA =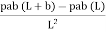
= 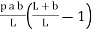
MA =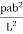
Special cases

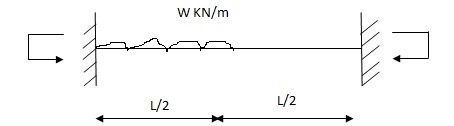
Q3) Explain the condition when fixed beam carrying partial udl.
A3) Fixed beam carrying partial udl
= 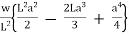
MA = 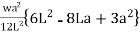
MB = 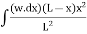
= 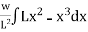
= 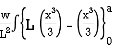
=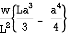
=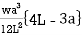
MB= 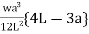
Special case:
MA = 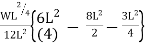
= 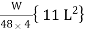
MB = 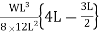
= 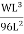
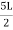
MB = 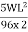
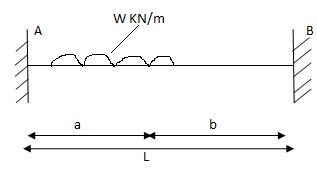
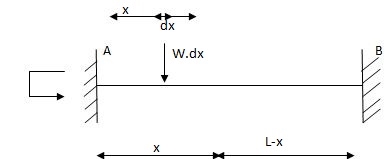
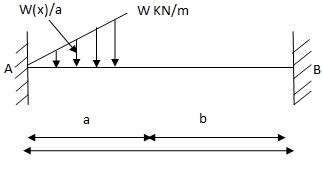
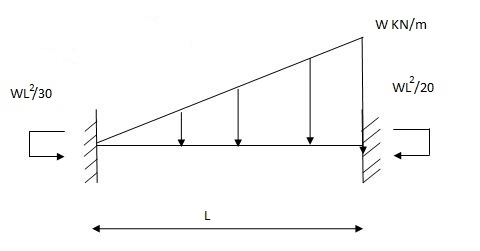
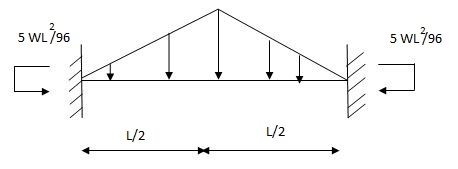
Q4) Explain the condition of fixed beam with partial UVL.
A4) Fixed beam with partial uvl
Diagram:
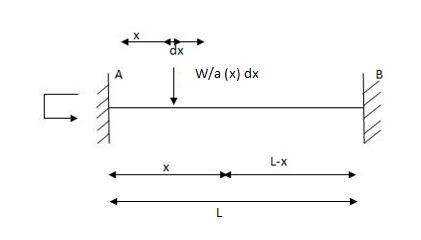
MB = 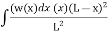
= w - 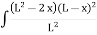
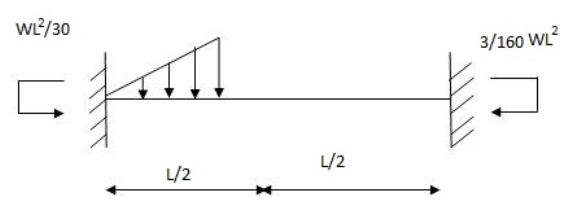
Q5) Explain the condition of fixed beam of sinking of support.
A5) Fixed beam with sinking of support (A)
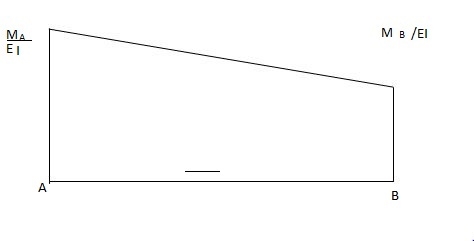
As per principle (1)
 Area of M dia. = 0
Area of M dia. = 0
 EI
EI

 (-) MA + MB (L) = 0
(-) MA + MB (L) = 0
2 EI
MA + MB = 0
MA = - MB (1)
As per principle (2)
 (AX) @ B =0
(AX) @ B =0

 tBA = (AX) @ B =
tBA = (AX) @ B =
 (-) L2 (2MA + MB) = (-)
(-) L2 (2MA + MB) = (-)
6EI
3M – LM2 = ………..From (1)
Final fig.
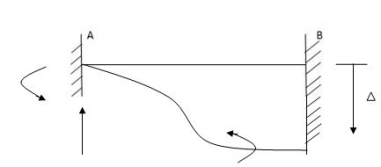
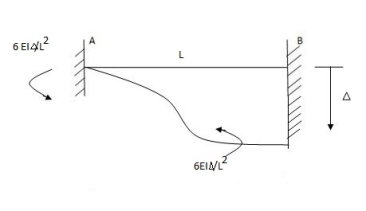
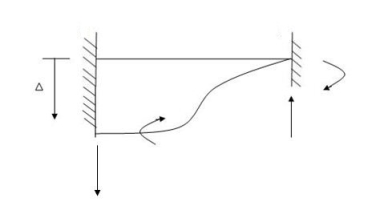
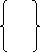
Q6) Explain the condition of fixed beam with rotational fielding.
A6) Fixed beam with rotational fielding
Diagram
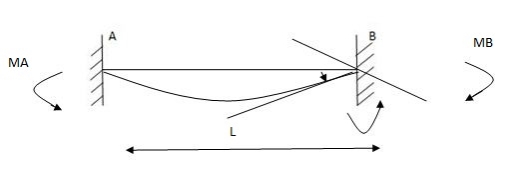
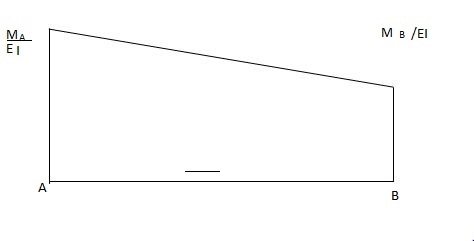
i) Area M dia. = B
 EI
EI
 (-1) 1 MA + MB (L) = B
(-1) 1 MA + MB (L) = B

 EI 2
EI 2
 MA + MB= (-) 2EI (B) (1)
MA + MB= (-) 2EI (B) (1)
 L
L

 Area M xXB = tBA = 0
Area M xXB = tBA = 0
E1

 (-) L2 2MA + MB = 0
(-) L2 2MA + MB = 0
6EI
 2MA + MB = 0 (2)
2MA + MB = 0 (2)
From (1)
…………..
2MA = 2EI (B) - MA = 0
 L
L
 MA = 2EI (B)
MA = 2EI (B)
 L
L

MB = 4 EI (B)
 L
L
For rotation B anticlockwise
(Both end moment & rotation clockwise)
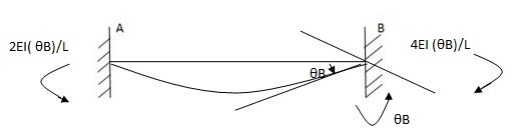
Q7) Explain the condition of fixed beam with couple.
A7) Fixed beam with couple
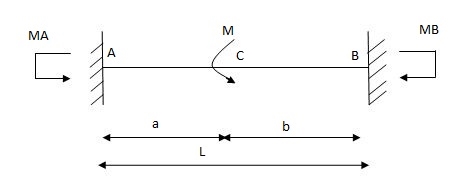
Area & (AX) (a) B

 A1 = 1 mA + mB (L)
A1 = 1 mA + mB (L)
 EI 2
EI 2



 A2 = 1 1 x ax m (a)
A2 = 1 1 x ax m (a)
EI 2 L
= ma2
 2LEI
2LEI

A3 = 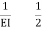 x b x
x b x (b)
(b)
= - mb2
 2 LEI
2 LEI


 (A x) 1 (a) B = (-) L2 2mA + mB
(A x) 1 (a) B = (-) L2 2mA + mB
6 EI



 (A x) 2 (a) B = (-) Ma2 b + 1 a
(A x) 2 (a) B = (-) Ma2 b + 1 a
2 LEI 3


 (A x) 3 (a) B = (-) Mb2 2 b
(A x) 3 (a) B = (-) Mb2 2 b
 2 LEI 3
2 LEI 3
= (-) Mb3
 3 LEI
3 LEI
As per principle (1)
Total Area = 0
∑ A = 0

 (-) mA + mB (L) + ma2 - mb2 - 0
(-) mA + mB (L) + ma2 - mb2 - 0

 2 2L 2L
2 2L 2L

 mA + mB (L) = m (a2 – b2)
mA + mB (L) = m (a2 – b2)
2 2L

 mA+ mB = m (a-b) (1)
mA+ mB = m (a-b) (1)
L
(3) (Ax) (a) B = 0
 (-) L2 (2 mA + mB) + ma2 b + a - mb3 = 0
(-) L2 (2 mA + mB) + ma2 b + a - mb3 = 0



 6 2L 3 3L
6 2L 3 3L

 2MA + MB= 6 (m) a2b+a - b3
2MA + MB= 6 (m) a2b+a - b3



 L2 2L 3 3L
L2 2L 3 3L
 2MA + MB = M 3a2b + a3 – 2b3
2MA + MB = M 3a2b + a3 – 2b3

 L (2)
L (2)
From (1),
 MB= M (a-b) - MA put in (2)
MB= M (a-b) - MA put in (2)
L


 2MA + M (a-b) – MA = M 3a2b + a3 – 2b3
2MA + M (a-b) – MA = M 3a2b + a3 – 2b3
L L3



 MA = M 3a2b + a3 – 2b3 - M (a-b)
MA = M 3a2b + a3 – 2b3 - M (a-b)
L3 L
 Multiply ÷ by ………….
Multiply ÷ by ………….
 MA = M 3a2b + a3 – 2b3 -(a-b) ( ………..)
MA = M 3a2b + a3 – 2b3 -(a-b) ( ………..)
L3

MA = M 3a2b + a3 – 2b3 -(a-b) ( ………..)
 L3
L3
 = M 2a2b – b3 – ab2
= M 2a2b – b3 – ab2
 L3
L3
MA = MB (a – o) (………….)
 L3
L3

 MA = MB (2 a-b)
MA = MB (2 a-b)
L3

 MB = M (a-b) - MB (2a-b)
MB = M (a-b) - MB (2a-b)
L L2

MB = (-) MQ (2b – a)
 L2
L2
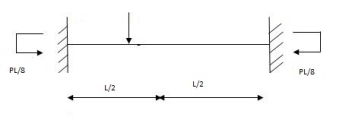
Q8) Explain the condition of couple at centre.
A8) Special case:
Couple at centre
B = 10mm (1)
E = 200 G pa
I = 8 x 106 mm4
EI = 1600 KN/M2
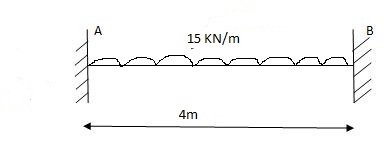
(1) FEM
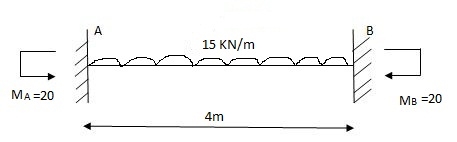
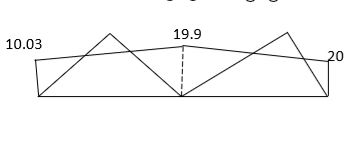
MA1 = (-) MB1 = WL2 = 15 X 16 = 20 KNM

 12 12
12 12
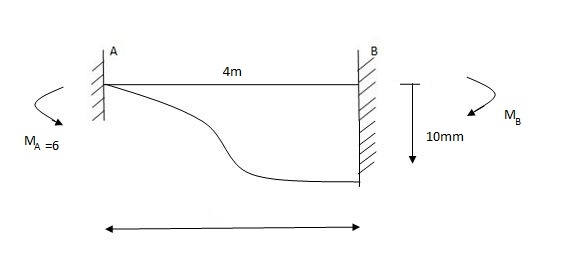
MA = MB
Final MA =?
MB =?
MA = VB (4) – 1
VA = 27
∑Fy = 0
VA /VA =
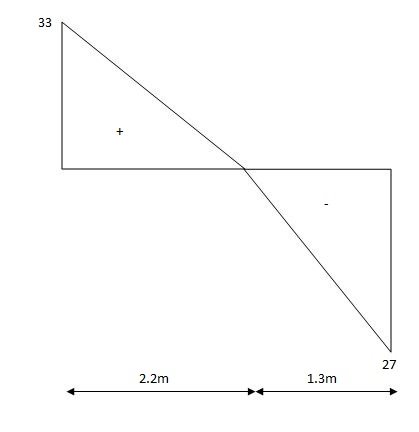
BMP
BMA= (-) 26 KNM
BMB = (-)19 KNM
 BMC = 33 (2.2) – 26 – 15 (2.2)2
BMC = 33 (2.2) – 26 – 15 (2.2)2
 Z
Z
BMC = 10.3 KNM
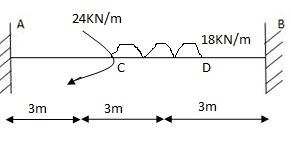
(1) FEM’S
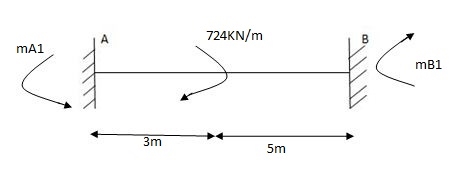
MA1= (-) Mb (2a-b)
 L2
L2
= (-) 24 x 5 (1)
 (8)2
(8)2
= (-) (1.875) KNM
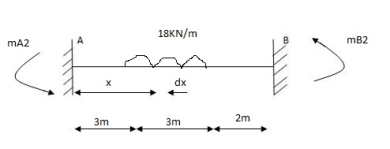
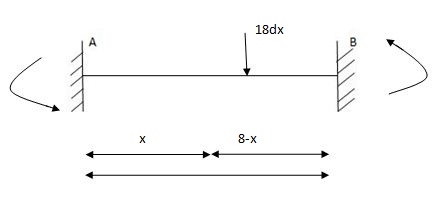
MA1 = 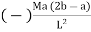
=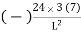
MA2= 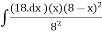
MA2= 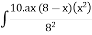
MA2 = 44.92 KNM
MB2 = (-) 56.320 KNM
MA = MA1 + MA2
= 1.875 + 44.92
MA = 43.045 KNM
MB = - 7.875 – 56.32 = - 64.195 KNM
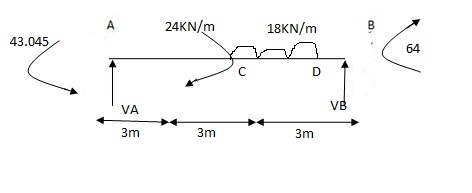
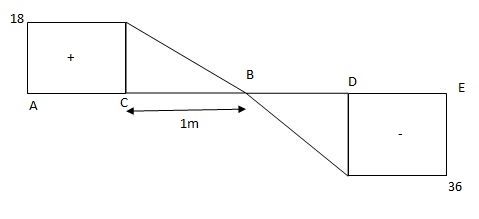
 X1 = y1 (a)
X1 = y1 (a)
 y1 + y2
y1 + y2
∑F y =VA + VB – 18 3 =0
 VA =17.98 x 18KN
VA =17.98 x 18KN
VA = 18KN
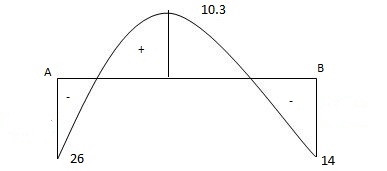
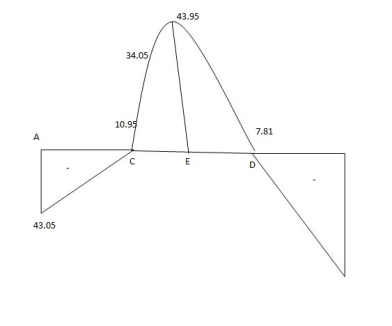
BMD

BMA = - 43.05 KNM
BMB = - 64.19 KNM
BMC(R) = 18 (3) – 43.05 = 10.95 KNM
BMC(R) = 10.95 + 24 = 34.95 KNM
BMF = 18 (4) – 43.05 + 24 - 18 = 43.95 KNM
 2
2
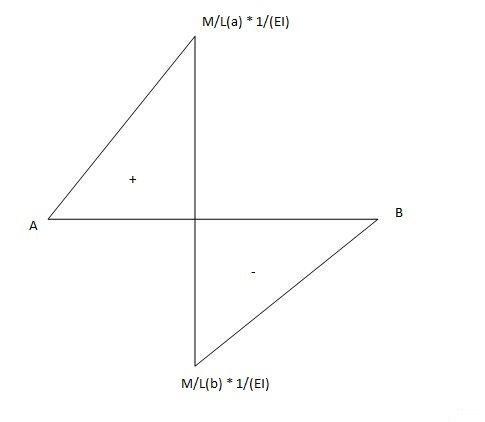
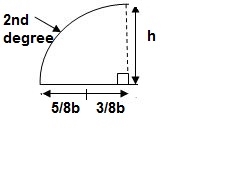
Q9) Explain moment area method in detail.
A9) Moment area method (Mohr’s Theorem):
Principle (I):
Angle between tangents drawn to elastic curve at any two points A & B is equal to area of M/EI diagram between A & B
Principle II:
Position of B on elastic curve with respect to tangent drawn at A is equal to moment of area of M/EI diagram between A & B about B.
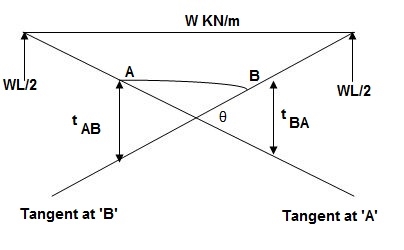
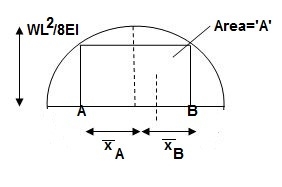
As per principle 1:ϴ = Area (A)
 Principle 2: t BA = (A) (xB)
Principle 2: t BA = (A) (xB)
Area and CG
For rectangle
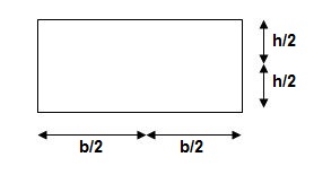
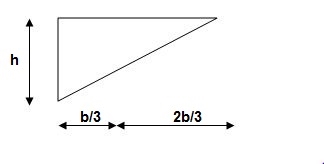
For parabola (udl)
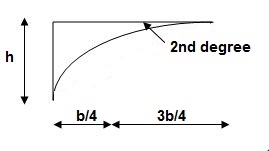
For cubic parabola (UVL Load)
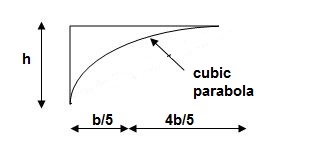
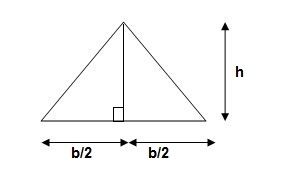
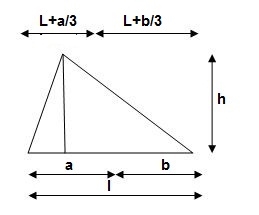
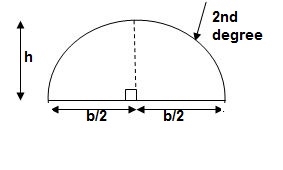
Q10) Find out slope and deflection at free end of cantilever.
A10) Derive slope & Deflection at free end of cantilever
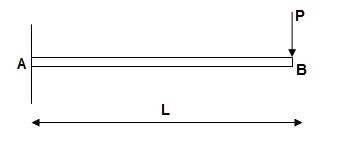
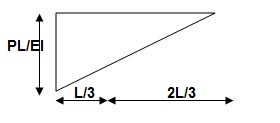
Solution:
ϴB = Area of (M/EL) AB
= ½ x L (PL/EI)
 ϴB = PL2/ZEI ( )
ϴB = PL2/ZEI ( )
t BA = ΔB = (Area)AB x xB
= (PL2/2EI) (2/3L)
 ΔB = PL3/3EI ( )
ΔB = PL3/3EI ( )
Q11) Find out slope and deflection of given beam.
A11)
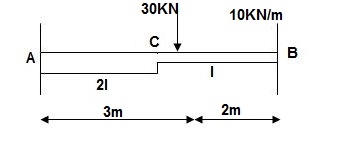
Find: ϴC, ΔC?
Solution:
BMD:
BM at c = 0
BMB = (-) 10 x 2 x 1
= (-) 20 KNM
BMA = (-) 30 x 3 – 10 x 2(4)
= (-) 170 KNM
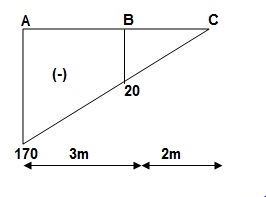
A1 = 30/EI
A2 = ½ x 75/EI x 3 = 112.5/EI
A3 = 1/3 x 2 x 20 x 20/EI = 13.33/EI
Elastic curve
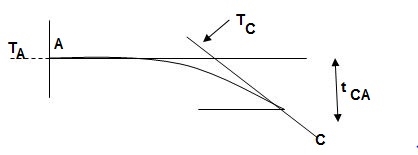
Slope & Deflection:
ϴC = Area of (M/EI) dia. |CA
ϴC = A1 + A2 + A3 = 1/EI {30 + 112.5 +13.33}
 ϴC = 155.83/EI ( )
ϴC = 155.83/EI ( )
ΔC = t CA = (A1x1 + A2x2 + A3x3) C
= 1/EI (30 x (3.5) + 112.5(2 + 2/3 x 3) + 13.33 (3/4 x 2))
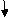 ΔC = 575/EI ( )
ΔC = 575/EI ( )
Q12) Find out ϴC& ΔC .
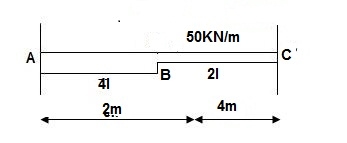
Find: ϴC&ΔC
A12)
E = 2 x 105 M Pa
I = 250 x 3503/12
EI = 1.78 x 105 KNm2
BMA = -50 x 4 x (2 + 2)
= - 800 KNM
BMB = -50 x 4 x 2
= -400 KNM
BMC = 0
BMD
M/EI Dia.:
A1 = 100 x 2/EI = 200/EI
A2 = 1/ 2x 100/EI x 2 = 100/EI
A3 = 1/3 x 200/EI x 4 = 266.67/EI
Elastic curve
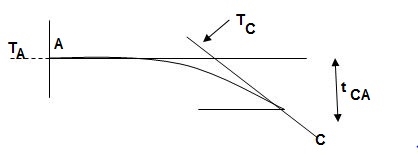
ϴC = Area of (M/EI) AC
= A1 + A2 + A3
= 200 + 100 + 266.67/EI
= 566.67/EI
 ϴC = 3.17 x 10-3 rad. ( )
ϴC = 3.17 x 10-3 rad. ( )
 ΔC = t CA = {Area}A-C x xC
ΔC = t CA = {Area}A-C x xC
= (A1x1 + A2x2 + A3x3)@C
= 200/EI x (4+1) + 100/EI x (4 + 2/3 x 2) + 266.67/EI(3/4 x 4)
= 1000/EI + 533.33/EI + 800.01/EI
= 2333.34/EI
= 13.1 x 10-3 m
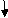 ΔC = 13.1 mm ( )
ΔC = 13.1 mm ( )
Q13) Find ϴC&ΔC
A13)
BMD
A1 = M/2EI x 3 = 1.5M/EI
A2 = M/EI x 3 = 3M/EI
ϴC = Area (M/EI) A-C
=A1 + A2
ϴC = 4.5M/EI
ΔC = t CA= (A1x1 + A2x2)@c
= 1.5M/EI x (3+1.5) + 3M/EI (1.5)
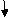 ΔC = 11.25M/EI ( )
ΔC = 11.25M/EI ( )
Q14) Find: ΔC
Find: ΔC
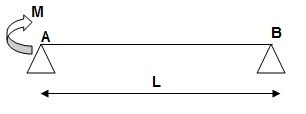
A14)
BMA = M
BMB = 0
BMD/‘M/EI Dia.
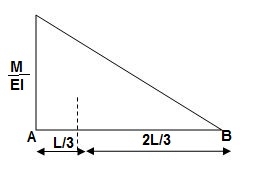
Elastic Curve
Slope & Deflection
 t AB = {Area}A-B x(xA)
t AB = {Area}A-B x(xA)
= 1 / 2 x M/EI x L {1/3L}
t AB = ML2/6EI
 t BA = {Area}A-B x(xB)
t BA = {Area}A-B x(xB)
= 1 / 2 x M/EI x L {2/3 L}
t BA = ML2/3EI
 ϴA ≈ tan (ϴA) = t BA/L = ML/3EI ( )
ϴA ≈ tan (ϴA) = t BA/L = ML/3EI ( )
 ϴB ≈ tan (ϴB) = t AB/L = ML/6EI ( )
ϴB ≈ tan (ϴB) = t AB/L = ML/6EI ( )
t AB/L = C1C3/L/2
C1C3 = t AB/2 = ML2/12EI
 t CB = Area C-B x (xc)
t CB = Area C-B x (xc)
= 1 / 2 x M/2EI x L/2 x {1/3 x L/2}
t CB = ML2/48EI
ΔC = C1– C2
= C1C3 – C2C3
= ML2/12EI – ML2/48EI
 ΔC = ML2/16EI ( )
ΔC = ML2/16EI ( )
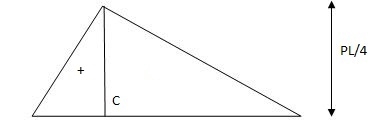
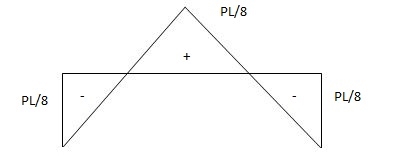
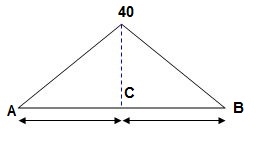
Q15) Find: ϴC, ΔC=?
Find: ϴC, ΔC=?
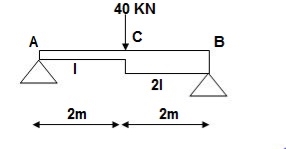
A15)
BMA = BMB = 0
BMC = PL/4
= 40 x 4/4
= 40 KNM
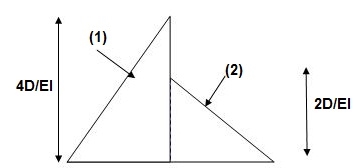
A1 = 1 / 2 x 2 x 40/EI = 40/EI
A2 = 1 / 2 x 2 x 20/EI = 20/EI
Elastic curve
Slope & Deflection
 t AB = (Area)A-B x xA
t AB = (Area)A-B x xA
(A1x1 + A2x2)@A
= 40/EI x (2/3 x 2) + 20/EI (2 + 1/3(2))
= 53.33/EI + 53.33/EI
t AB = 106.67/EI
 t BA = {Area}AB x xB
t BA = {Area}AB x xB
= (A1x1 + A2x2)@B
= 1/EI {40 x (2 + 1/32) + 20(2/3 x 2)}
= 133.33/EI
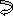 ϴA ≈ tan (ϴA) = t BA/L = 133.33/4EI = 33.33/EI ( )
ϴA ≈ tan (ϴA) = t BA/L = 133.33/4EI = 33.33/EI ( )
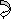 ϴB ≈ tan (ϴB) = tan AB/L = 106.67/4EI = 26.67/EI ( )
ϴB ≈ tan (ϴB) = tan AB/L = 106.67/4EI = 26.67/EI ( )
For ΔC (C1, C2)
t AB/4 = C1C3/2
C1C3 = t AB/2 = 106.67/2EI = 53.33/EI
 t CB = {Area}CB x (xC)
t CB = {Area}CB x (xC)
= 20/EI x (1/3 x 2) = 13.33/EI
ΔC = C1C3 – C2C3
= 53.33 – 13.33
ΔC = 39.99/EI
 ΔC = 40/EI ( )
ΔC = 40/EI ( )
Q16) Find: ϴA& ΔC?
A16)
∑MA = 0
-50 x 1 + VB x 4 + 20 = 4VB = 30
VB = 7.5 KN
VA + VB = 50
VA = 42.5KN
BMA = 0
BMB = 0
BMC = 42.5 x 1 = 42.5 KNM
BMDL = 42.5 x 3 – 50 x 2 = 27.5 KNM
BMDR = 7.5 x (1) = 7.5 KNM
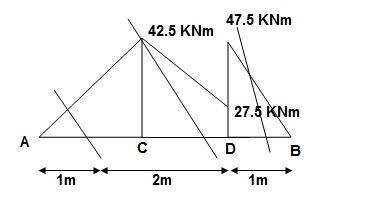
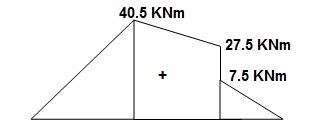
A1 = 1 / 2 x 1 x 42.5/EI = 21.25/EI
A2 = 1 / 2 x 2 x 15/EI = 15/EI
A3 = 27.5/EI x 2 = 55/EI
A4 = 7.5/2EI x 1 = 3.75/EI
Elastic curve:
Slope &Deflection:
 t AB = {Area}A-B x xA
t AB = {Area}A-B x xA
= (A1x1 + A2x2 + A3x3 + A4x4)@A
= 21.25/EI x [2/3 x (1)] + 15/EI(1 + 1/3 x 2) + 55/EI(1 + 1)+ 3.75/EI(3 + 1/3 x 1)
= 14.16/EI + 25/EI + 110/EI + 12.5/EI
= 161.66/EI
 t BA = Area(B-A) x xB
t BA = Area(B-A) x xB
= {A1x1 + A2x2 + A3x3 + A4x4}@B
= 1/EI {21.25(3 + 1/3 x 1) + 15(1 + 2/3 x 2) + 55(2) + 3.75 x 2/3}
= 218.33/EI
ϴA ≈ tan (ϴA) = t BA/4
 ϴA = 218.33/4EI = 54.58/EI ( )
ϴA = 218.33/4EI = 54.58/EI ( )
 ϴB ≈ tan (ϴB) = t AB/4 = 161.66/4EI = 40.41/EI ( )
ϴB ≈ tan (ϴB) = t AB/4 = 161.66/4EI = 40.41/EI ( )
To find ΔC
t BA/4 = C1C3/1
C1C3 = 54.58/EI
 C1C2 = t CA = Area CA x xC
C1C2 = t CA = Area CA x xC
= A1xC
= 21.25/EI (1/3 x 1)
= 7.08/EI
ΔC = C1C3– C1C2
 = 54.58/EI – 7.08/EI
= 54.58/EI – 7.08/EI
= 47.5/EI ( )
Q17) Explain slope and deflection method in detail.
A17)
Slope deflection methods: means it is a method or tool by which we find out how a structure or a member of a structure behaves when subjected to certain excitation.
In other words finding out internal forces (axial force, shear force, moment), stress, strain, deflection, etc in a structure under applied load conditions.
Fixed End Moments: Standard Cases Fixed End Moments
Standard Cases
1.
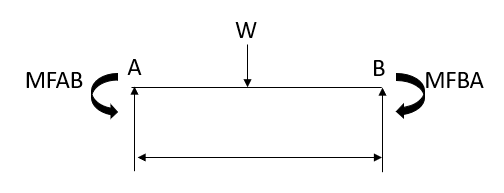
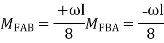
2.
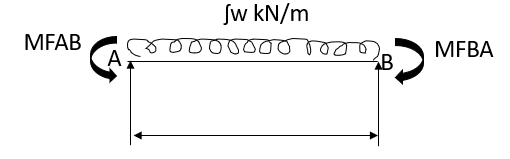
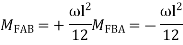
3.
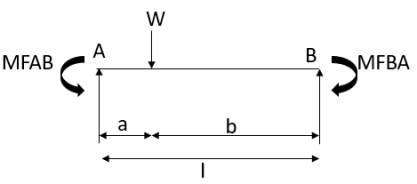
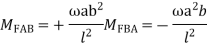
4.
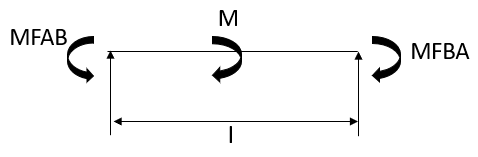
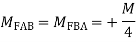
5.
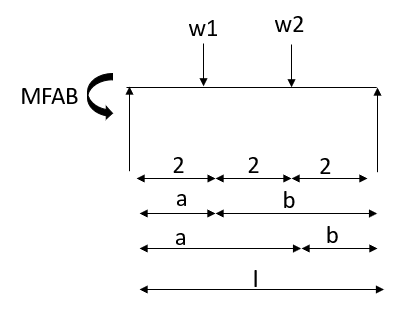
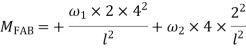
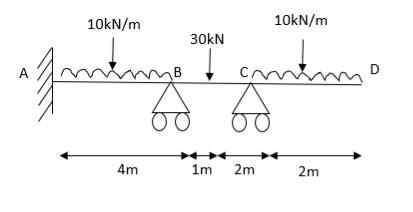
Q18) Analyze the continuous beam ABCD by S.D. method draw BMD
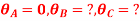
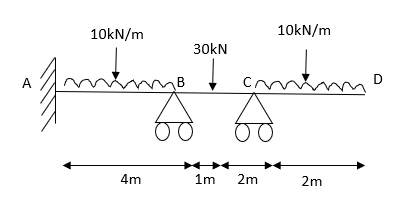
A18) Modify Diagram
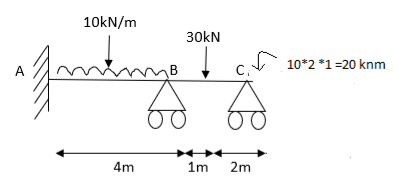
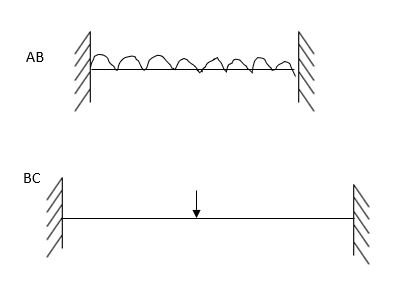
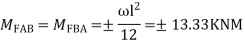
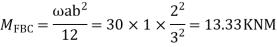
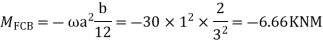
Apply S.D. equation
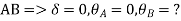
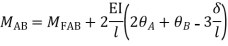
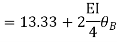
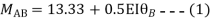
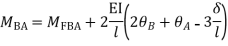
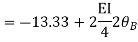
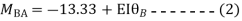
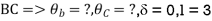
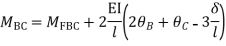
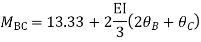
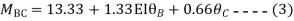
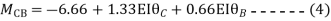
Joint equilibrium equation
Joint at B