Unit – 6

Linear Prediction Coding

Q1) What is the LPC model of speech production?

Ans: LPC model of speech production

With the block diagram shown in Figure, linear prediction coding relies on a highly simplified model for speech processing. The model is based on observations of basic speech signal properties and is an attempt to replicate the human speech processing mechanism. The synthesis filter represents the combined spectral contributions of the glottal flow, the vocal tract, and the lip radiation.

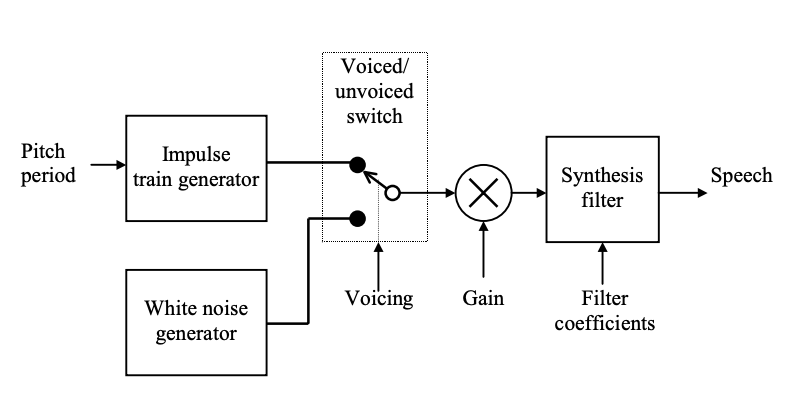
Fig 1: The LPC model of speech production

The filter's or excitation signal's driving input is modeled as either an impulse train (voiced speech) or random noise (unvoiced speech). As a result, the switch is set to the appropriate position based on whether the signal is voiced or unvoiced, allowing the appropriate input to be selected. The gain parameter controls the output's energy level.

Take a look at speech samples that have been divided into non-overlapping frames. The signal's properties effectively remain constant for a short enough frame duration. The model's parameters are estimated from the speech samples in each frame, in this case, the parameters are as follows:

●      Voicing: whether the frame is voiced or unvoiced.

●      Gain: mainly related to the energy level of the frame.

●      Filter coefficients: specify the response of the synthesis filter.

●      Pitch period: in the case of voiced frames, time length between consecutive excitation impulses.

For each frame, the parameter estimation process is repeated, with the results reflecting the frame's knowledge. As a result, instead of sending PCM samples, model parameters are sent. An amazing compression ratio can be achieved by carefully allocating bits for each parameter to minimize distortion.

For example, the FS1015 coder's bit rate of 2.4 kbps is 53.3 times lower than the corresponding bit rate for 16-bit PCM. The cost is an irreversible reduction in efficiency. In many practical applications, however, high-quality reproduction is not needed.

The encoder is in charge of estimating the parameters. The decoder synthesizes speech using the approximate parameters and the speech processing model. The method of using noise to produce the output signal is a little perplexing. How will the scheme work if the output waveform looks nothing like the original? In fact, since the white noise generator is random, output waveforms using the same set of parameters and filter initial conditions differ.

It's worth noting that the synthesis filter captures the original speech's power spectral density; as a result, the PSD of the synthetic speech is similar to the original due to the flat spectrum of input excitation. The method discards the original waveform's phase information, leaving only the magnitude of the frequency spectrum.

Since phase information has a lower rank than magnitude information for a human listener, the synthetic waveform sounds identical to the original. The signal-to-noise ratio is a low and often meaningless indicator of speech quality because of this phenomenon.

This violation of the AR model for voiced signals is examined as one of the LPC model's fundamental limitations for speech processing. The excitation impulse train is given by

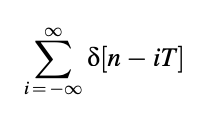
With ,

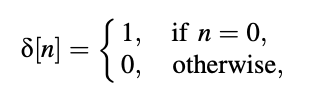
T is a positive constant that represents the time. A periodic impulse train is used to generate periodicity in the output waveform, resulting in a signal with a PSD that resembles voiced signals.

Since the synthesis filter coefficients must be quantized and transmitted, only a few of them are measured in order to keep the bit rate low. This prediction order is sufficient for unvoiced frames; however, due to the correlation of distant samples, a much higher order is expected for voiced frames.

The LPC coder solves this by using an impulse train input: if the input excitation's time matches the original pitch, periodicity is applied to the synthetic speech with a PSD that is close to the original. As a result, high prediction order is avoided, and the low bit-rate target is met.

Q2) What is the structure of the encoder?

Ans:  The encoder's block diagram is shown in the diagram. Second, the input speech is divided into non overlapping frames. The range of the input signal is adjusted using a pre-emphasis filter.

The voicing detector, which is addressed in the following section, determines if the current frame is voiced or unvoiced and outputs one bit to indicate the voicing state.

The pre-emphasized signal is used in the LP review, which yields ten LPCs.

The indices transmitted as frame information are used to quantize these coefficients. The quantized LPCs are used to build the prediction-error filter, which filters the pre-emphasized speech and outputs the prediction-error signal.

If and only if the frame is articulated, the pitch time is determined from the prediction-error signal. Since the formant structure (spectrum envelope) due to the vocal tract is eliminated when the prediction-error signal is used as input to the pitch time estimation algorithm, a more accurate approximation can be obtained.

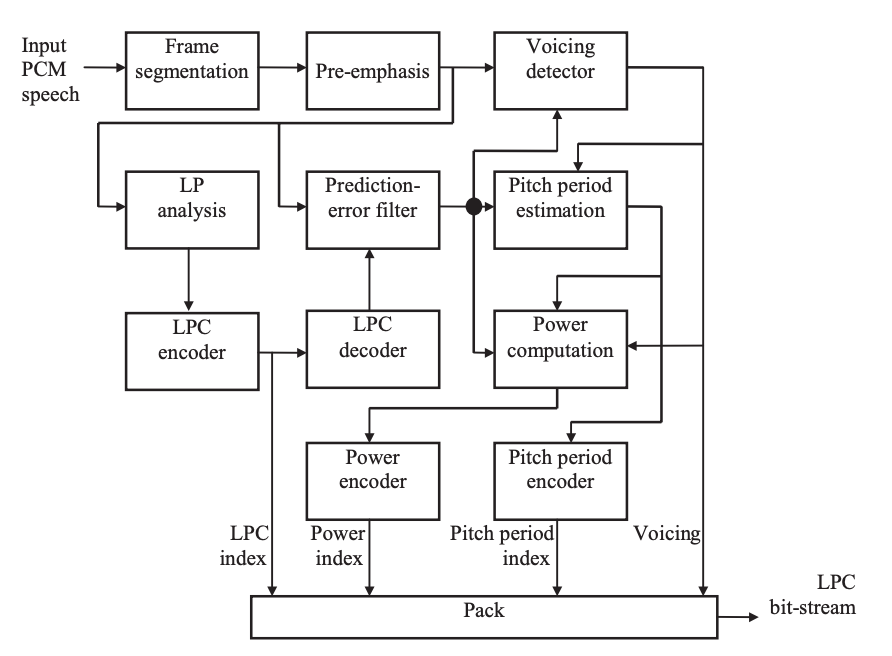
Fig 2: Block diagram of the LPC encoder

Q3) Illustrate limitations of LPC model?

Ans: Limitations of the LPC model

The LPC coder's overly simplistic model has a low computational cost, allowing for the implementation of a low bit-rate speech coder. The simple model, on the other hand, is extremely inaccurate in a variety of situations, resulting in distracting artifacts in synthetic expression. These drawbacks will be addressed by the next generation of speech coders.

LIMITATION 1: In many instances, a speech frame cannot be classified as strictly voiced or strictly unvoiced.

The LPC model does not correctly sort any transition frames (voiced to unvoiced and unvoiced to voiced). The model's inaccuracy causes distracting artifacts like buzzes and tonal noises.

LIMITATION 2: The use of strictly random noise or a strictly periodic impulse train as excitation does not match practical observations using real speech signals.

The excitation signal is obtained by filtering the speech signal with the prediction-error filter and can be used in practice as prediction error. White noise can be used to estimate the excitation for unvoiced frames in general. The excitation signal for voiced frames, on the other hand, is a combination of a quasiperiodic variable and noise.

As a result, using an impulse train is a crude approximation that degrades synthetic speech's naturalness. Furthermore, the quasiperiodic excitation portion often has a changing duration, and the pulse form is not quite an impulse. The excitation pulses for the FS1015 coder are produced by using an impulse train to excite an allpass filter.

LIMITATION 3: No phase information of the original signal is preserved.

The LPC model does not capture phase information, as we have seen: neither voiced nor unvoiced frames have explicit parameters containing phase clues. Since the magnitude range, or power spectral density, of the synthetic speech is close to that of the original signal, it sounds natural. Even though a human listener is relatively unaffected by phase, keeping some phase information in the synthetic speech adds naturalness and improves accuracy.

It's worth noting that, since noise perception is basically phaseless, phase information for unvoiced frames can be overlooked during speech synthesis by the LPC decoder. Not so much for voiced pictures, where a non-smooth pitch time contour appears irregular and distorted. As a result, maintaining a (ideally) continuous pitch contour is needed for voiced frames synthesis so that transitions (normally of varying pitch periods) are as transparent as possible.

LIMITATION 4: The approach used to synthesize voiced frames, where an impulse train is used as excitation to a synthesis filter with coefficients obtained by LP analysis, is a violation of the foundation of AR modeling.

The violation causes spectral distortion in the synthesized voice, which gets worse as the pitch time gets shorter. For low-pitch-period or high-pitch frequency talkers, such as women and infants, the LPC coder does not function well. However, for the average male, spectral distortion is mild, and the LPC coder can produce acceptable output.

Q4) What is the structure of the decoder?

Ans: structure of decoder

The decoder's block diagram, which is basically the LPC model of speech production with parameters regulated by the bit-stream, is shown in Figure. The impulse train generator's output is presumed to be a sequence of unit amplitude impulses, while the white noise generator's output is assumed to be unit-variance.

The following is how the gain is calculated. For the unvoiced case, the synthesis filter's input power must be the same as the encoder's prediction error. We have g as a symbol for the gain.

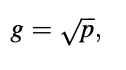
since the white noise generator has unit-variance output.

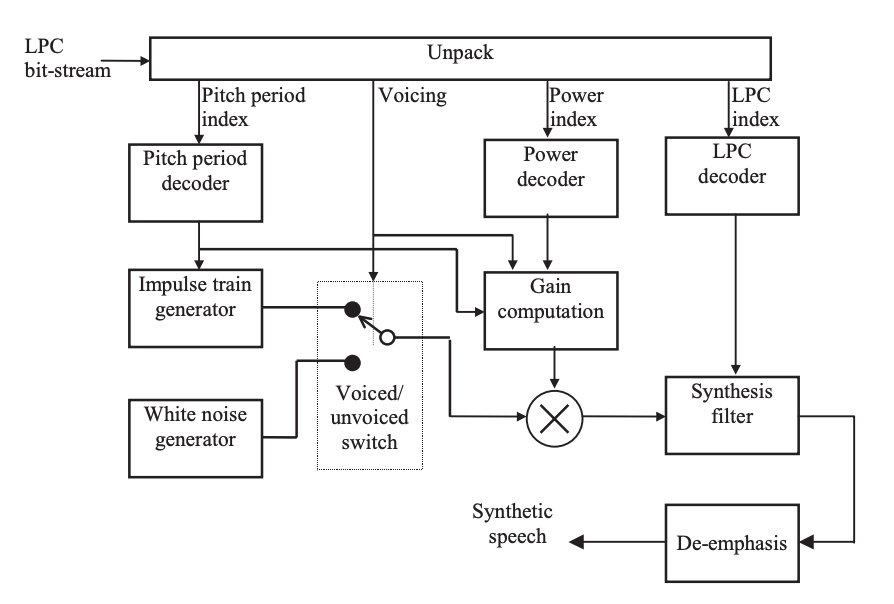
Fig 3: Block diagram of the LPC decoder

The power of an impulse train with an amplitude of g and a time of T, calculated over an interval of length [NIT]T, must equal p in the voiced case. Doing the procedure results in

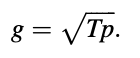
Finally, the synthesis filter's output is de-emphasized to produce synthetic expression.

Q5) Describe voice detection?

Ans: The voicing detector's job is to determine if a frame is voiced or not. In certain cases, determining whether a frame is voiced or unvoiced can be done simply by looking at the waveform: a frame with consistent periodicity is labeled as voiced, whereas a frame with a noise-like appearance is labeled as unvoiced.

However, in some cases, the distinction between voiced and unvoiced is blurred; this occurs during transition frames, as the signal switches from voiced to unvoiced or vice versa. One of the LPC model's most significant flaws is the need for a strict voiced/unvoiced classification.

In order to achieve a high degree of robustness, the detector must take into account as many parameters as possible. These parameters are fed into a binary-output linear classifier. Since misclassification of voicing states can have catastrophic effects on the quality of synthetic expression, the voicing detector is one of the most important components of the LPC coder.

Energy

This is the most clear and straightforward sign of "voicedness." Voiced sounds are usually many orders of magnitude more energetic than unvoiced signals. The energy is given by the frame (of length N) ending at instant m.

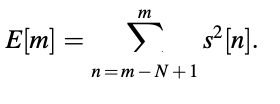
The magnitude sum function defined by is used for simplicity.

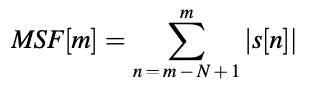
serves the same function.

Lowpass filtering the speech signal prior to energy measurement will improve discrimination because voiced speech has energy concentrated in the low-frequency area due to the comparatively low value of the pitch frequency. That is to say, only the energy of low-frequency components is considered.

Zero Crossing Rate

The frame ending at time instant m has a zero crossing rate described by

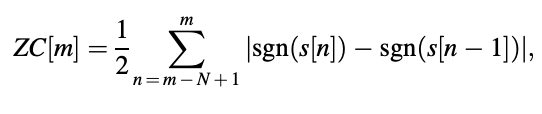
The sign function returns 土1 depending on the sign of the operand with sgn(.). A zero crossing is defined as when successive samples have different signs.

The zero crossing rate for voiced speech is low due to the existence of the pitch frequency component (of low-frequency nature), while the zero crossing rate for unvoiced speech is high due to the signal's noise-like appearance and a large portion of energy located in the high-frequency field.

Prediction Gain

The energy of the signal divided by the energy of the prediction error.

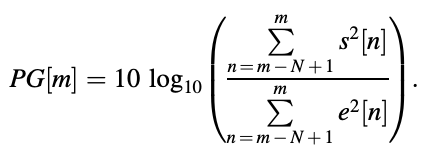
Voiced frames achieve a prediction benefit of 3 dB or more on average than unvoiced frames, owing to the fact that periodicity means higher sample correlation and hence more predictability. Unvoiced frames, on the other hand, are less predictable because they are more spontaneous.

To prevent numerical problems, prediction gain is usually not measured for very low-amplitude frames; in this case, the frame can be allocated as unvoiced simply by checking the energy level.

Voicing Detector Design

The parameters discussed thus far (energy, zero crossing rate, etc.) can be used by a voicing detector to make the appropriate decision. With only one parameter as input, a simple detector can be developed. The zero crossing rate, for example, can be used to detect voicing in the following way: if the rate is less than a certain threshold, the frame is voiced; otherwise, it is unvoiced.

The design issue is thus to determine the appropriate threshold for making a reliable voicing decision. It is possible to come up with a fair value for a judgment threshold by evaluating a large number of speech signals in order to minimize the overall classification error.

However, relying on only one parameter limits the system's robustness. Noise contamination may cause the zero crossing rate of the voicing detector to increase, causing voiced frames to be counted as unvoiced frames. As a result, more frame parameters must be used to increase voicing detection efficiency.

Consider the frame's parameters grouped into a type vector.

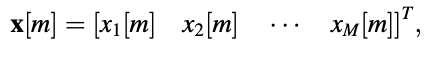
corresponding to the time instant m at which the frame ends. The vector's elements are the frame's parameters, which can be any of the previously described quantities. The elements of the vector are used by the voicing detector to make the appropriate decision.

This is a pattern classification problem, in which the pattern vector is categorized into two categories: voiced and unvoiced.

To accomplish the voicing detection job, a pattern classifier based on a linear combiner is a simple and effective process. The frame that ends at time m is labeled using this method.

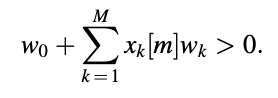
The frame is declared voiced if the quantity is greater than zero; otherwise, it is unvoiced. Finding the proper set of weights wk, k = 0,..., M simplifies the problem of voicing detector architecture.

The parameters of interest are derived and processed by processing a vast volume of speech data frame by frame. A human observer classifies each frame as voiced or unvoiced; that is, the human operator determines the voicing status based on a visual assessment of the waveform. The desired answer for which the pattern classifier is programmed is based on the human operator's decisions.

Q6) Write the application of LPC?

Ans: Application of LPC

●      In speech coding and synthesis, LPC is the most widely used process. It's also used for speech synthesis and analysis. Phone companies, for example, use it as a method of voice compression in the GSM standard. It's also used for protected wireless, where voice has to be digitized, encrypted, and transmitted over a small voice channel; the US government's Navajo I is an early example of this.

●      Musical instruments can be used as an excitation signal to a time-varying filter calculated from a singer's voice, and LPC synthesis can be used to create vocoders. This is a common occurrence in electronic music. Using linear predictive coding, Paul Lansky transformed the well-known computer music piece into something more than idle chatter.

●      Shorten, MPEG-4 ALS, FLAC, SILK audio codec, and other lossless audio codecs use LPC predictors.

●      LPC is gaining traction as a method for analyzing the tonal characteristics of violins and other stringed instruments.

Q7) What are the limitations of LPC?

Ans: Limitations of LPC

The efficiency of the LPC is constrained by both the method and the signal's local characteristics.

●      The spectral envelope is sub-sampled by the harmonic spectrum, resulting in spectral aliasing. These issues are most noticeable in voiced and high-pitched signals, and they affect the signal's first harmonics, which relate to perceived speech quality and formant dynamics.

●      It's difficult to get a good all-pole model for the signal spectrum.

●      We get too close to the original spectra to reflect the desired spectral detail, the spectral envelope. The LPC follows the spectrum's curve all the way down to the residual noise level in the space between two harmonics, or partials that are too far apart. It does not reflect the desired spectral information to be modeled since we are only interested in fitting the spectral envelope to the original spectra as closely as possible.

●      Instead of the "valleys" created by the harmonic peaks, the spectral envelope should be a smooth function moving through the prominent peaks of the spectrum, yielding a flat series.

Q8) Write the principle of LPC?

Ans: Principle of LPC

●      First, input and output sequences are observed, resulting in a model with a number of poles, or formants.

●      The resulting set of coefficients can then be used to define the behavior of an unknown system. It is used to predict the outcome of a study. This set of coefficients is an all-pole model, which is a simplified version of the speech production system's acoustic model.

●      The values of a discrete-time signal are then estimated as a linear function of previous samples. Using the information from the linear predictive model, the spectral envelope is expressed in compressed form.