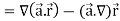Unit-4
Multivariable Calculus (Differentiation)
Question-1: (i) Evaluate 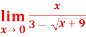
Ans 1)
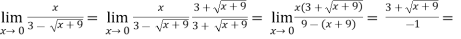 -6.
-6.
(ii) Evaluate 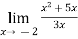
Sol.
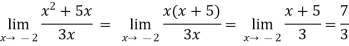
Question-2: Calculate 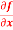 and
and 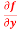 for the following function
for the following function
f(x , y) = 3x³-5y²+2xy-8x+4y-20
Ans 2) To calculate 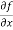 treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
treat the variable y as a constant, then differentiate f(x,y) with respect to x by using differentiation rules,
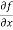 =
= 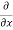 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 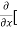 3x³] -
3x³] - 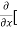 5y²] +
5y²] + 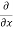 [2xy] -
[2xy] -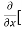 8x] +
8x] +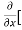 4y] -
4y] - 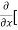 20]
20]
= 9x² - 0 + 2y – 8 + 0 – 0
= 9x² + 2y – 8
Similarly partial derivative of f(x,y) with respect to y is:
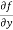 =
= 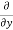 [3x³-5y²+2xy-8x+4y-20]
[3x³-5y²+2xy-8x+4y-20]
= 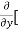 3x³] -
3x³] - 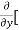 5y²] +
5y²] + 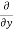 [2xy] -
[2xy] -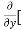 8x] +
8x] +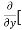 4y] -
4y] -  20]
20]
= 0 – 10y + 2x – 0 + 4 – 0
= 2x – 10y +4.
Question-3: if 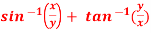 , then show that-
, then show that- 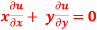
Ans 3) Here we have,
u = 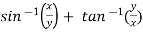 …………………..(1)
…………………..(1)
now partially differentiate eq.(1) w.r to x and y , we get
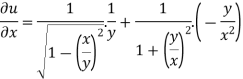
= 
Or

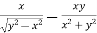 ………………..(2)
………………..(2)
And now,

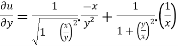
= 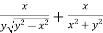
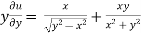 ………………….(3)
………………….(3)
Adding eq. (1) and (3) , we get
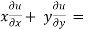
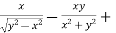
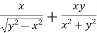 = 0
= 0
Hence proved.
Question-4: Find the directional derivative of
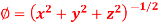
At the points (3, 1, 2) in the direction of the vector 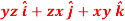 .
.
Ans 4) Here it is given that-
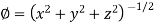
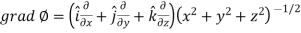
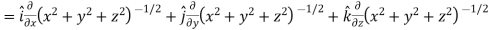

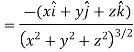
Now at the point (3, 1, 2)-
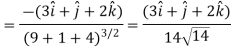
Let 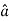 be the unit vector in the given direction, then
be the unit vector in the given direction, then
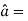
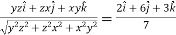 at (3, 1, 2)
at (3, 1, 2)
Now,


Question-5: let q = 4x + 3y and x = t³ + t² + 1 , y = t³ - t² - t
Then find 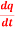 .
.
Ans 5)
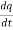 . =
. = 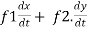
Where, f1 =  ,f2 =
,f2 = 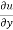
In this example f1 = 4 , f2 = 3
Also,
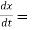 3t² + 2t ,
3t² + 2t , 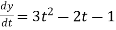
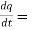 4(3t² + 2t) + 3(
4(3t² + 2t) + 3(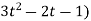
= 21t² + 2t – 3
Question-6: if w = x² + y – z + sint and x + y = t, find
(a)  y,z
y,z
(b) 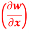 t, z
t, z
Ans 6) With x, y, z independent, we have
t = x + y, w = x² + y - z + sin (x + y).
Therefore,
 y,z = 2x + cos(x+y)
y,z = 2x + cos(x+y)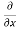 (x+y)
(x+y)
= 2x + cos (x + y)
With x, t, z independent, we have
Y = t-x, w= x² + (t-x) + sin t
thus 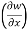 t, z = 2x - 1
t, z = 2x - 1
Question-7: If z is the function of x and y , and x =  , y =
, y = 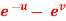 , then prove that,
, then prove that,
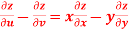
Ans 7) Here , it is given that, z is the function of x and y & x , y are the functions of u and v.
So that,
 ……………….(1)
……………….(1)
And,
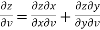 ………………..(2)
………………..(2)
Also there is,
x = 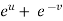 and y =
and y =  ,
,
now,
 ,
, 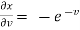 ,
, 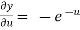 ,
, 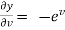
From equation(1) , we get
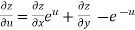 ……………….(3)
……………….(3)
And from eq. (2) , we get
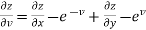 …………..(4)
…………..(4)
Subtracting eq. (4) from (3), we get
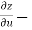
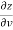 =
= 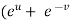 )
)  – (
– (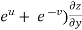
= x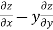
Hence proved.
Question-8: Find the equation of the tangent plane and normal line to the surface 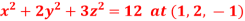
Ans 8)
Here,
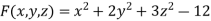
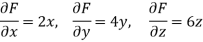
At point (1, 2, -1)-
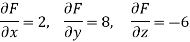
Therefore the equation of the tangent plane at (1, 2, -1) is-
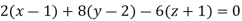
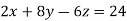

Equation of normal line is-
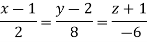
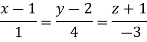
Question-9: Find out the maxima and minima of the function

Ans 9)
Given  …(i)
…(i)
Partially differentiating (i) with respect to x we get
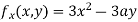 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
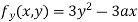 ….(iii)
….(iii)
Now, form the equations 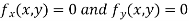
Using (ii) and (iii) we get
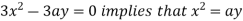
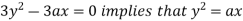
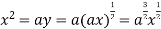 using above two equations
using above two equations
Squaring both side we get
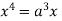
Or 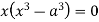
This show that 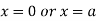
Also we get 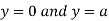
Thus we get the pair of value as 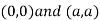
Now, we calculate
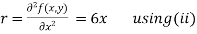
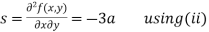
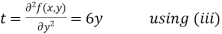
Putting above values in

At point (0,0) we get
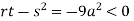
So, the point (0,0) is a saddle point.
At point 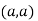 we get
we get
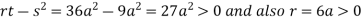
So the point 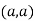 is the minimum point where
is the minimum point where 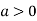
In case 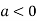
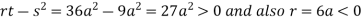
So the point 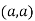 is the maximum point where
is the maximum point where 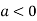
Question-10: If 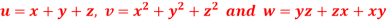 then prove that grad u, grad v and grad w are coplanar.
then prove that grad u, grad v and grad w are coplanar.
Ans 10)
Here- 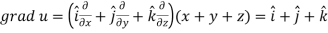
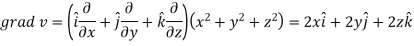
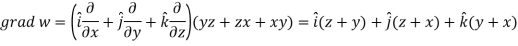
Now-
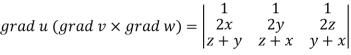
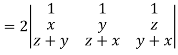
Apply 
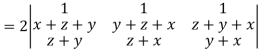
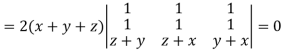
Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Question-11: If 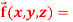
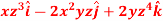 then find the divergence and curl of
then find the divergence and curl of 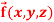 .
.
Ans 11) We know that-
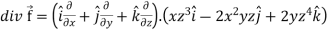
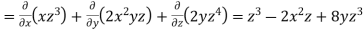
Now-

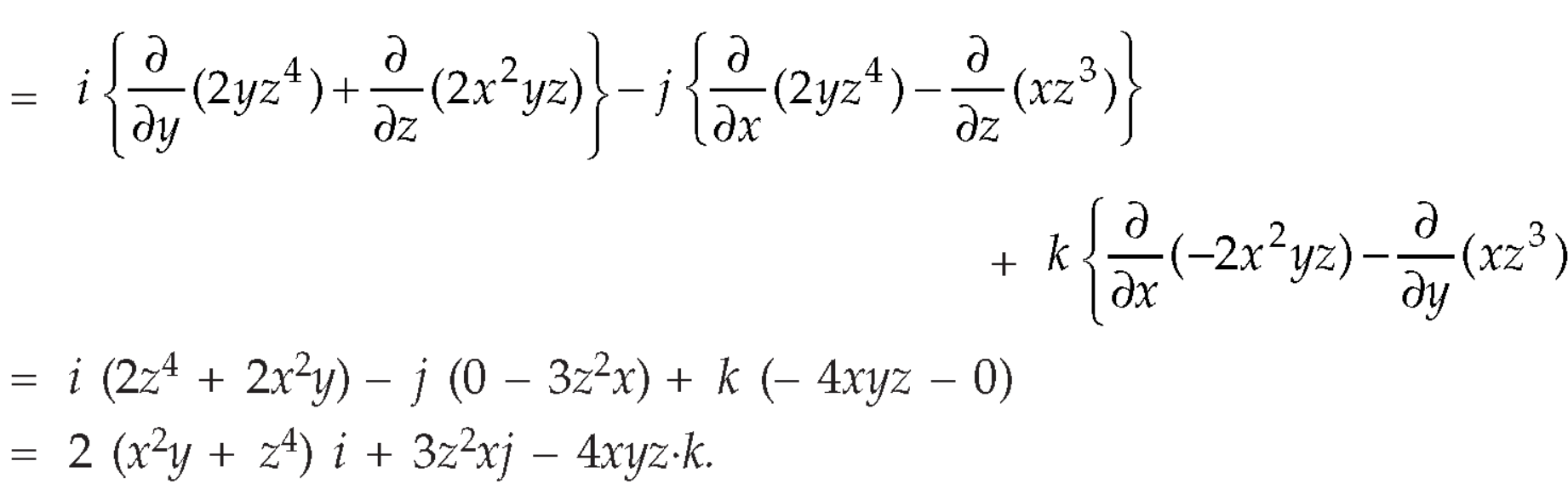
Question-12: Prove that 
Note- here  is a constant vector and
is a constant vector and 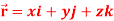
Ans 12) here 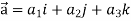 and
and 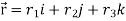
So that
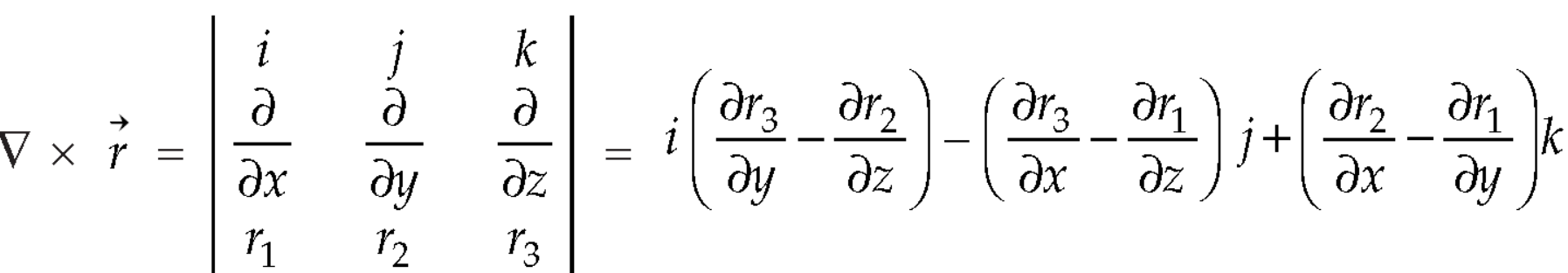
Now-
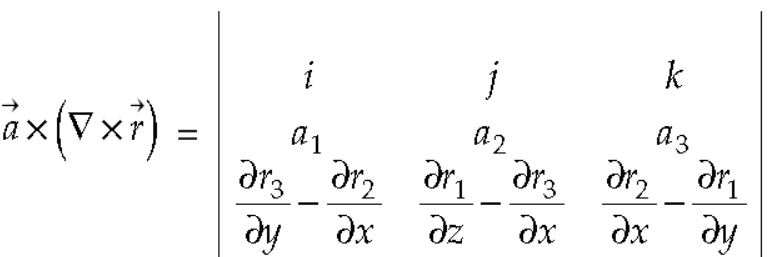
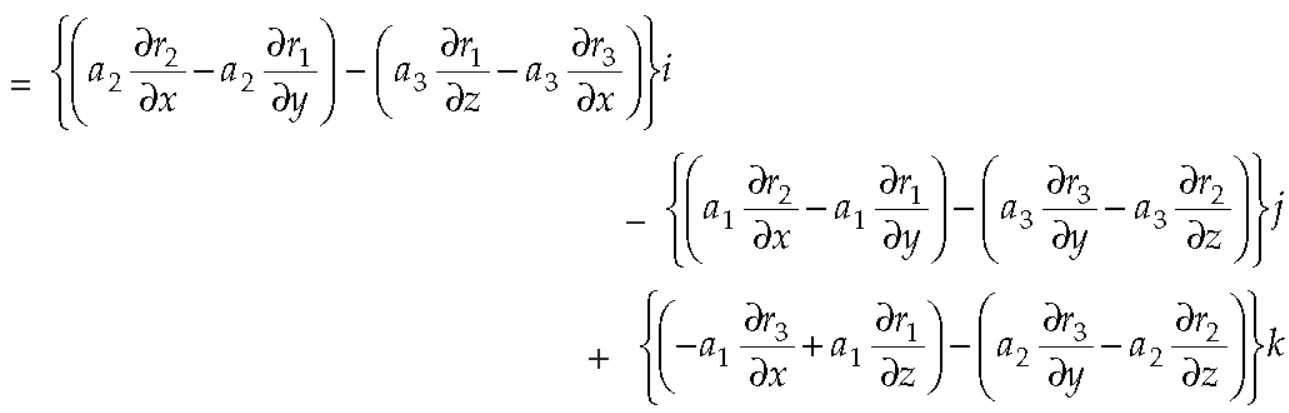
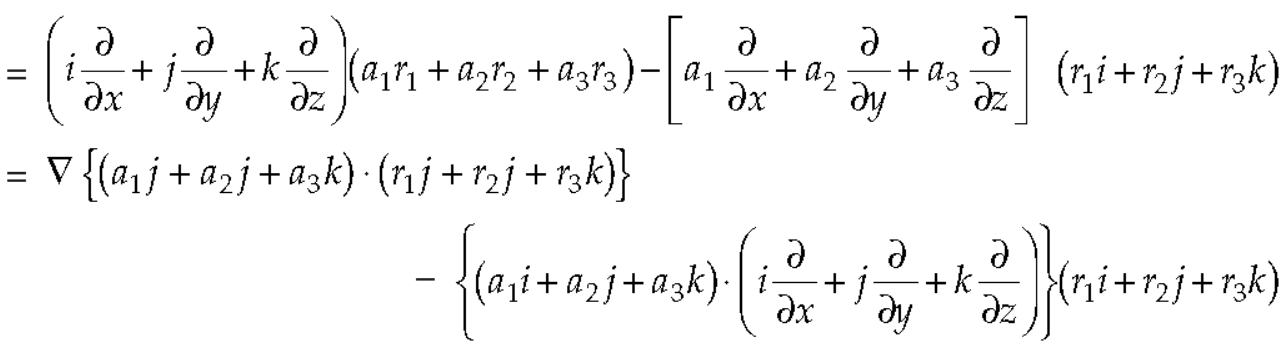
So that-