Unit – 4

Sections and Sectional Views of Right Angular Solids

Q1) Explain the step for Auxiliary Views in solids?

A1) Invisible features of an object are shown by dotted lines in their projected views. But when such features are too many, these lines make the views more complicated and difficult to interpret. In such cases, it is customary to imagine the object as being cut through or sectioned by planes. The part of the object between the cutting plane and the observer is assumed to be removed and the view is then shown in section.

The imaginary plane is called a section plane or a cutting plane. The surface produced by cutting the object by the section plane is called the section. It is indicated by thin section lines uniformly spaced and inclined at 45°.

The projection of the section along with the remaining portion of the object is called a sectional view. Sometimes, only the word section is also used to denote a sectional view.

(1) Section planes:

Section planes are generally perpendicular planes. They may be perpendicular to one of the reference planes and either perpendicular, parallel or inclined to the other plane. They are usually described by their traces. It is important to remember that the projection of a section plane, on the plane to which it is perpendicular, is a straight line. This line will be parallel, perpendicular or inclined to xy, depending upon the section plane being parallel, perpendicular or inclined respectively to the other reference plane.

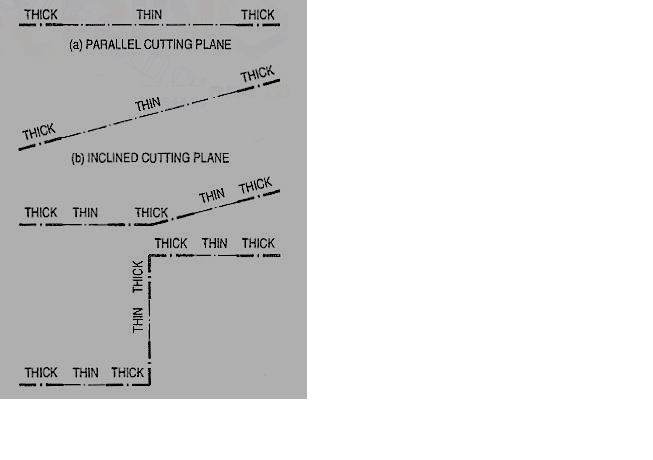
As per latest 8.1.S. Convention (SP: 46-2003), the cutting-plane line should be drawn as shown in fig.

(2) Sections: The projection of the section on the reference plane to which the section plane is perpendicular, will be a straight-line coinciding with the trace of the section plane on it. Its projection on the other plane to which it is inclined is called apparent section. This is obtained by

(i) projecting on the other plane, the points at which the trace of the section plane intersects the edges of the solid and

(ii) drawing lines joining these points in proper sequence.

(3) True shape of a section: The projection of the section on a plane parallel to the section plane will show the true shape of the section. Thus, when the section plane is parallel to the H.P. Or the ground, the true shape of the section will be seen in sectional top view. When it is parallel to the V.P., the true shape will be visible in the sectional front view.

But when the section plane is inclined, the section must be projected on an auxiliary plane parallel to the section plane, to obtain its true shape. When the section plane is perpendicular to both the reference planes, the sectional side view will show the true shape of the section. In this chapter sections of different solids are explained in stages by means of typical problems as follows:

1. Sections of prisms

2. Sections of pyramids

3. Sections of cylinders

4. Sections of cones

5. Sections of spheres.

Q2) Explain the steps on sections of prisms?

A2) These are illustrated according to the position of the section plane with reference to the principal planes as follows:

(1) Section plane parallel to the V.P.

(2) Section plane parallel to the H.P.

(3) Section plane perpendicular to the H.P. And inclined to the V.P.

(4) Section plane perpendicular to the V.P. And inclined to the H.P.

Q3) Write the step on Sections of Cones?

A3) (1) Section plane parallel to the base of the cone.

(2) Section plane passing through the apex of the cone.

(3) Section plane inclined to the base of the cone at an angle smaller than the angle of inclination of the generators with the base.

(4) Section plane parallel to a generator of the cone.

(5) Section plane inclined to the base of the cone at an angle greater than the angle of inclination of the generators with the base.

Q4) A cube of 35 mm long edges is resting on the H.P. On one of its faces with a vertical face inclined at 30° to the V.P. It is cut by a section plane parallel to the V.P. And 9 mm away from the axis and further away from the V.P. Draw its sectional front view and the top view.

A4) In fig the section plane is assumed to be transparent and the cube is shown with the cut-portion removed. Four edges of the cube are cut and hence, the section is a figure having four sides.

Draw the projections of the whole cube in the required position [fig.2(ii)]. As the section plane is parallel to the V.P., it is perpendicular to the H.P.; hence, the section will be a line in the top view coinciding with the H.T. Of the section plane.

(i) Draw a line H.T. In the top view (to represent the section plane) parallel to xy and 9 mm from o.

(ii) Name the points at which the edges are cut, viz. Ab at 1, be at 2, gf at 3 and fe at 4.

(iii) Project these points on the corresponding edges in the front view and join them in proper order.

As the section plane is parallel to the V.P., figure 1' 2' 3' 4' in the front view, shows the true shape of the section.

Show the views by dark but thin lines, leaving the lines for the cut-portion fainter.

(iv) Draw section lines in the rectangle for the section.

Q5) A triangular prism, base 30 mm side and axis 50 mm long, is lying on the H.P. On one of its rectangular faces with its axis inclined at 30° to the V.P. It is cut by a horizontal section plane, at 12 mm above the ground. Draw its front view and sectional top view.

A5) As the section plane is horizontal, i.e., parallel to the H.P., it is perpendicular to the V.P. Hence, the section will be a line in the front view, coinciding with the V. T. Of the section plane.

(i) Therefore, draw a line V.T. In the front view to represent the section plane, parallel to xy and 12 mm above it.

(ii) Name in correct sequence, points at which the edges are cut viz. a'b' at 1 ', a'c' at 2', d'f' at 3' and d'e' at 4'.

(iii) Project these points on the corresponding lines in the top view and complete the sectional top view by joining them in proper order.

As the section plane is parallel to the H.P., the figure 1 2 3 4 (in the top view) is the true shape of the section.

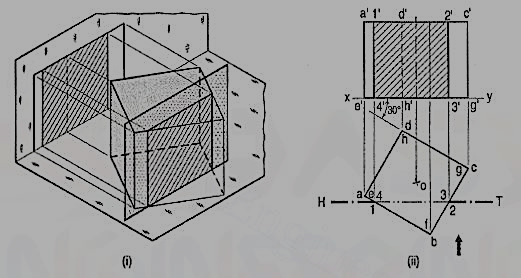
Q6) A cube in the same position as in problem 1, is cut by a section plane, inclined at 60° to the V.P. And perpendicular to the H.P., so that the face which makes 60° angle with the V.P. Is cut in two equal halves. Draw the sectional front view, top view and true shape of the section.

A6) The section will be a line in the top view coinciding with the H.T. Of the section plane.

(i) Draw the projections of the cube. Draw a line H.T. In the top view inclined at 60° to xy and cutting the line ad (or be) at its mid-point.

(ii) Name the corners at which the four edges are cut and project them in the front view. As the section plane is inclined to the V.P., the front view of the section viz. 1' 2' 3' 4' does not reveal its true shape. Only the vertical lines show true lengths, while the true lengths of the horizontal lines are seen in the top view. The true shape of the section will be seen when it is projected on an auxiliary vertical plane, parallel to the section plane.

(iii) Therefore, draw a new reference line x1y1 parallel to the H.T. And project the section on it. The distances of the points from x1y1 should be taken equal to their corresponding distances from xy in the front view. Thus 4" and 3" will be on x1y1. 1" 4" and 2" 3" will be equal to 1' 4' and 2' 3' respectively. Complete the rectangle 1" 2" 3"4" which is the true shape of the section and draw section lines in it.

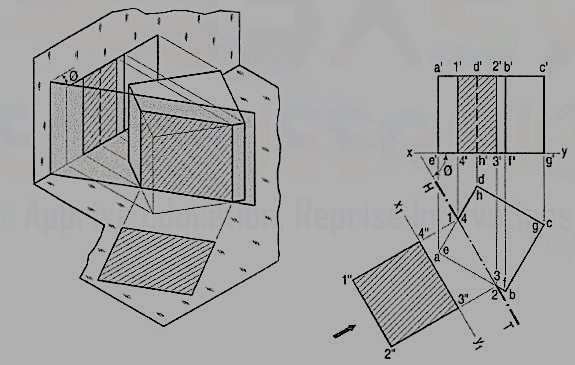
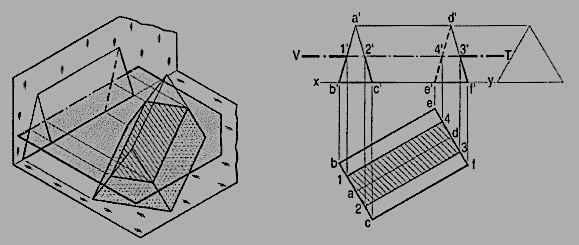
Q7) A cube in the same position as in problem 14-1 is cut by a section plane, perpendicular to the V.P., inclined at 45° to the H.P. And passing through the top end of the axis. (i) Draw its front view, sectional top view and true shape of the section. (ii) Project another top view on an auxiliary plane, parallel to the section plane.

A7) The section will be a line in the front view.

(i) Draw a line V.T. In the front view, inclined at 45° to xy and passing through the top end of the axis. It cuts four edges, viz. a' e' at 1 ', a' b' at 2', c'd' at 3' and d'h' at 4'.

(ii) Project the top view of the section, viz. The figure 1 2 3 4. It does not show the true shape of the section, as the section plane is inclined to the H.P. To determine the true shape, an auxiliary top view of the section should be projected on an A.I.P. Parallel to the section plane.

(iii) Assuming the new reference line for the A.I.P. To coincide with the V.T., project the true shape of the section as shown by quadrilateral 11 21 31 41. The distances of all the points from the V.T. Should be taken equal to their corresponding distances from xy in the top view, e.g., 111' = e'1, 414' = h'4 etc.

(iv) To project an auxiliary sectional top view of the cube, draw a new reference line x1 y1, parallel to the V.T. The whole cube may first be projected and the points for the section may then be projected on the corresponding lines for the edges. Join these points in correct sequence and obtain the required top view.

(v) Draw section lines in the cut-surface, in the views where it is seen. Keep the lines for the removed edges thin and fainter.

Sections of Pyramids:

The following cases are discussed in details.

(1) Section plane parallel to the base of the pyramid.

(2) Section plane parallel to the V.P.

(3) Section plane perpendicular to the V.P. And inclined to the H.P.

(4) Section plane perpendicular to the H.P. And inclined to the V.P.

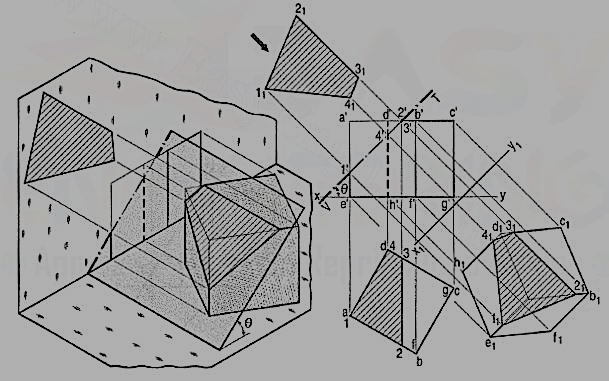
Q8) A square pyramid, base 40 mm side and axis 65 mm long, has its base on the H.P. And all the edges of the base equally inclined to the V.P. It is cut by a section plane, perpendicular to the V.P., inclined at 45° to the H.P. And bisecting the axis. Draw its sectional top view, sectional side view and true shape of the section.

A8)

(i) Draw the projections of the pyramid in the required position. The section plane will be seen as a line in the front view. Hence, draw a line V.T. Through the mid-point of the axis and inclined at 45° to xy. Name in correct sequence the points at which the four edges are cut and project them in the top view. Here also, points 2' and 4' cannot be projected directly.

Hence, assume a horizontal section through 2' and draw a line parallel to the base, cutting o' a' at 2'1. Project 2'1 to 21 on oa in the top view. From 21 draw a line parallel to ab and cutting ob at a point 2. Or, with o as centre and radius o 21, draw an arc cutting ob at 2 and ob at 4. Complete the section 1 2 3 4 by joining the points and draw section lines in it.

(ii) Assuming the V.T. To be the new reference line, draw the true shape of the section. Project the side view from the two views. The removed portion of the pyramid may be shown by thin and faint lines.

Q9) A cylinder of 40 mm diameter, 60 mm height and having its axis vertical, is cut by a section plane, perpendicular to the V.P., inclined at 45° to the H.P. And intersecting the axis32 mm above the base. Draw its front view, sectional top view, sectional side view and true shape of the section.

A9)

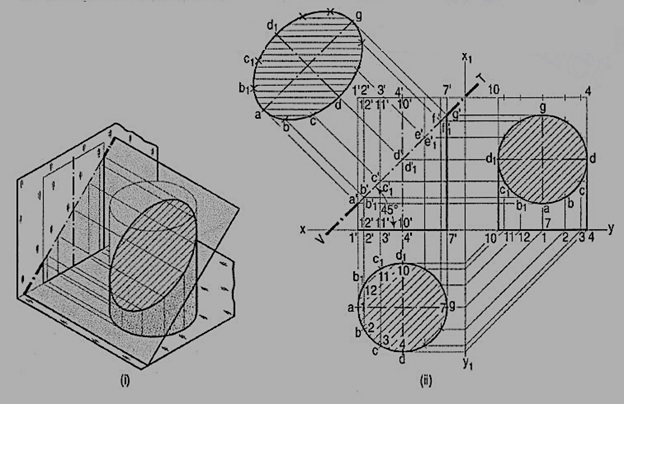
As the cylinder has no edges, many lines representing the generators may be assumed on its curved surface by dividing the base-circle into, say 12 equal parts.

(i) Name the points at which these lines are cut by the V.T. In the top view, these points lie on the circle and hence, the same circle is the top view of the section. The width of the section at any point, say c', will be equal to the length of the chord cc1 in the top view.

(ii) The true shape of the section may be drawn around the center line ag drawn parallel to V.T. As shown. It is an ellipse the major axis of which is equal to the length of the section plane viz. a'g', and the minor axis equal to the diameter of the cylinder viz. Dd1.

(iii) Project the sectional side view as shown. The section will be a circle because the section plane makes 45° angle with xy.

Sections of Cones:

(1) Section plane parallel to the base of the cone.

(2) Section plane passing through the apex of the cone.

(3) Section plane inclined to the base of the cone at an angle smaller than the angle of inclination of the generators with the base.

(4) Section plane parallel to a generator of the cone.

(5) Section plane inclined to the base of the cone at an angle greater than the angle of inclination of the generators with the base.

(1) Section plane parallel to the base of cone:

The cone resting on the H.P. On its base [fig.] is cut by a section plane parallel to the base. The true shape of the section is shown by the circle in the top view, whose diameter is equal to the length of the section viz. a'a'. The width of the section at any point, say b', is equal to the length of the chord bb1.

Q10) A cone, base 45 mm diameter and axis 55 mm long is resting on the H.P. On its base. It is cut by a section plane, perpendicular to both the H.P. And the V.P. And 6 mm away from the axis. Draw its front view, top view and sectional side view.

A10) The section will be a line, perpendicular to xy, in both the front view and the top view. The side view will show the true shape of the section. The width of the section at any point, say c', will be equal to cc1 obtained by the circle method [fig. (i) Draw the side view of the cone.

(ii) Project the points (on the section) in the side view taking the widths from the top view. For example, through c' draw a horizontal line. Mark on it points c" and c"1 equidistant from and on both sides of the axis so that c" c"1 = cc1.

(iii) Draw a curve through the points thus obtained. It will be a hyperbola.

Shows the views obtained by the generator method.

Sections of Spheres:

(1) Section plane parallel to the H.P.

(2) Section plane parallel to the V.P.

(3) Section plane perpendicular to the V.P. And inclined to the H.P.

(4) Section plane perpendicular to the H.P. And inclined to the V.P.