Module -1
Basic Probability
Question and Answer
- In poker, a full house (3 cards of one rank and two of another, e.g. 3 fours and 2 queens) beats a flush (five cards of the same suit).
Solution- A player is more likely to be dealt a flush than a full house. We will be able to precisely quantify the meaning of “more likely” here.
2. A coin is tossed repeatedly.
Solution- Each toss has two possible outcomes:
Heads (H) or Tails (T)
Bothequally likely. The outcome of each toss is unpredictable; so is the sequence of H and T.
3. A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
Solution- We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for 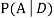 . We know:
. We know:

Now,
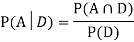
So we need
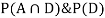
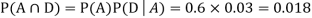
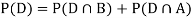
Since, D is the union of the mutually exclusive events  and
and  (the entire sample space is the union of the mutually exclusive events A and B)
(the entire sample space is the union of the mutually exclusive events A and B)
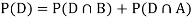

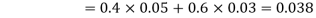
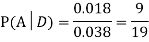
4. Two fair dice are rolled, 1 red and 1 blue. The Sample Space is
S = {(1, 1),(1, 2), . . . ,(1, 6), . . . ,(6, 6)}.Total -36 outcomes, all equally likely (here (2, 3) denotes the outcome where the red die show 2 and the blue one shows 3).
(a) Consider the following events:
A: Red die shows 6.
B: Blue die shows 6.
Find  ,
,  and
and  .
.
Solution:
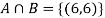

NOTE: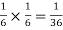 so
so  for this example. This is not surprising - we expect A to occur in
for this example. This is not surprising - we expect A to occur in  of cases. In
of cases. In  of these cases i.e. in
of these cases i.e. in 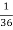 of all cases, we expect B to also occur.
of all cases, we expect B to also occur.
5. You are given a bag of marble. Inside the bag are 5 red marble, 4 white marble, 3 blue marble. Calculate the probability that with 6 trials you choose 3 marbles that are red, 1 marble that is white and 2 marble is blue. Replacing each marble after it is chosen.
Solution:


6. You are randomly drawing cards from an ordinary deck of cards. Every time you pick one you place it back in the deck. You do this 5 times. What is the probability of drawing 1 heart, 1 spade, 1club, and 2 diamonds?
Solution:
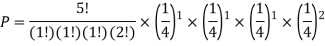
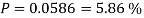
7. A plant places biscuits into boxes of 100. The probability that a biscuit is cracked is 0.03. Find the probability that a box contains 2 cracked biscuits
Solution
This is a binomial distribution by means of n = 100 besides p = 0.03.
These standards are external the range of the counters and include lengthy calculations.
Using the Poisson estimate (test: np = 100 x 0.3 = 3, which is less than 5)
Let X be the random variable of the number of cracked biscuits
The mean λ = np = 100 × 0.3 = 3
P(X = 2) = 0.224 (from counters)
8. If the probability that a light bulb is defective is 0.8, what is the probability that the light bulb is not defective?
Solution:
Probability that the bulb is defective, p = 0.8
Probability that the bulb is not defective, q = 1 - p = 1 - 0.8 = 0.2
9. The effect of the degree of risk on the portfolio is illustrated as follows: Portfolio risk is measured in this example when the correlation of the coefficients is -1, 1.5, -0.5, 9, + 1 when x = - 1, the risk is the lowest, the risk would be zero if the percentage of inversion in values X1 and Xj is modified so that the standard deviation becomes 0 and x = -1.
(i)When 

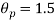
(ii)When 
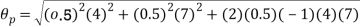

(iii)When 

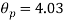
(iv)When, 
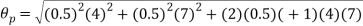
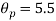
10. ![[eq13]](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1714217405_222458.png)
Let  be a random variable such that
be a random variable such that
Find a lower bound to its variance.
Solution
The lower bound can be derived thanks to Chebyshev's inequality:
