Unit – 1
Review Of Semiconductor Physics
Question and Answer
1) State E-K Diagram?
Answer:
Definition :An E-k diagram shows features of a particular semiconductor material. It shows the relationship between the energy(E) and momentum(p) of available quantum powered states for electrons in the material
Explanation:
The blue circle bend line shows the valence band while black circlecurve shows the conduction band .
Eg, known as energy band gap of Conduction and Valence band as well.
cogitate a basic E-k band figure like this one (the x-axis can be either momentum, p, or wave number, k, since p=ℏk
The E-k diagram of a direct band gap semiconductor such as GaAs.
The curve involves of many discrete points with each point matching to a possible state, the wave functionΨk(x), that is allowed to exist in the crystal.
The points are so close that we customarily draw the E-k relationship as a continuous curve.
2) Explain Density Of State with suitable graph and diagram?
Answer:
The density of states (DOS) is principally the number of unlike states at a particular energy level that electrons are permissible to occupy, i.e. the number of electron states per unit volume per unit energy or i.e. number of permissible state per unit volume per unit energy interval.
Bulk properties such as specific heat, paramagnetic susceptibility(χ), and other transport phenomena of conductive solids be contingent on this function.
DOS controls allow one to limit the general distribution of states as a function of energy and can also determine the spacing amid energy bands in semi-conductors.
Density of state is directly relational to root of energy given in overhead map here, E=
, P known as momentum and m is mass.
A free electron has a velocity (v) and a momentum( p) =m v . Its energy E encloses totally of kinetic energy (V=0) ,so
P2/2m
De-Broglie, hypothesised that if waves might exhibit particle-like belongings, then might particles also display wave-like properties?
This idea is expressed as particle-wave dual nature and allows us to give the electron a wave number k ,ђ(reduced Planck’s constant)
k =
These are the Heisenberg uncertainty principle and the Pauli exclusion principle.
Together, these two rules nasty that the wavefunction ( ) for the electron must satisfy the Schrödinger equation, subject to border conditions.
The answer of the Schrödinger equation leads to wavefunctions() of the form:
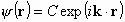
The explanation of the Schrödinger equation leads to wavefunctions () of the form:
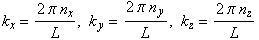
Where n x , n y , n z are integers.
3) What do you understand by Probability of occupation?
Answer:
Fermions such as, electrons shadow a, Fermi–Dirac distribution and bosons such as, phonons and photons track, a Bose–Einstein distribution
Occupation probability of the electronic states near W1.
Band assembly from above figure along three different momentum directions near the Weyl points (W1) in TaAs.
The black and red dashed dotted lines in each panel fits to the Fermi level and the energy of W1 ( 2 MeV), respectively.
The colour maps, which are calculated from the Fermi-Dirac distribution function f(E), denote the occupation probability of the electronic states at different temperatures(T) of 5 K (a to c), 150 K (d to f) and 300 K (g to i).
The red arrows represent the electronic transitions at the energy of the A 1 mode.
The thickness of each arrow schematically show the change amplitude.
We have equation of 4 dimensional i.e. 0D(Dot),1D(Wire),2D(Slab),3D(Bulk) along with numeral and equation in Probability of occupation
4) State Fermi Level and Quasi Fermi Level with the help of carrier concentration and temperature?
Answer:
Definition:When a semiconductor is in Thermal equilibrium, the supply function of the electrons at the energy level of E is presented by a Fermi –Dirac delivery function.
In this case the Fermi level is defined as the level in which the probability of work of electron at that energy is ½.
In thermal equipoise, there is no need to distinguish between conduction band quasi-Fermi level and valence band quasi-Fermi level as they are simply equivalent to the Fermi level.
The electron in conduction band which is in equilibrium is given by
ne = Neffe · exp – | EC – EF kT |
The holes in valance band which is in symmetry is given by
nh = Neffh · exp – | EF – EV kT |
Balance means -holes and electron are equal in band this resources fermi energy is same or equal for both bands
Carrier Concentration:
Now for the equation of Fermi we must write down f(E, EFe, T) or f(E, EFh, T) instead of f(E,Ef,T) or E f
.
The carrier concentration of electron or holes in conduction or valance band are as follow
ne = Neffe · [fe in C(E, EFe, T)]Neffe · exp - 
The carrier concentration of electron or holes in conduction or valance band are as follow
ne = Neffn · [fn in C(E, EFn, T)]Neffn · exp - 
This can be cured easily by simply setting 1 – f(E, EFh, T) =: fh in V(E, EFh, T) with fh in V existence the probability of finding holes on the available states in the valence band.
Formally, the electron density in the valence band (EV) then contains 1 – fh in V and so on.
5) Define P-N Junction diode? Draw suitable diagram and explain it?
Answer:
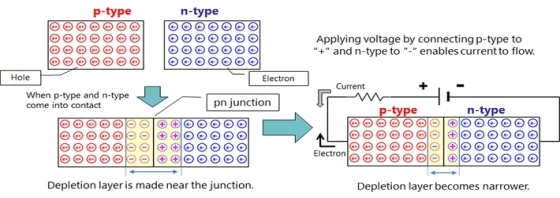
Definition: A p-n junction is an interface or a boundary between two semiconductor material types, namely the p-type and the n-type, inside a semiconductor.
p type semiconductor have hole as majority carrier while minority carrier electron
similarly n type have majority electron and minority carrier hole
When p-type and n-type come into contact depletion layer is made near the junction.
Connecting battery positive terminal at p type and n type then we can get narrower depletion layer this kind of bias is know as forward bias while after changing terminal we can get reverse bias.
Flow of electron and current are opposite to each other.
6) Explain Metal Semiconductor Junction by Ohmic and Schottky?
Answer:
Whenever a metal and a semiconductor come together, thereemerging of a potential barrier between the two that prevents most charge electrons or holes from passing from one to the other.
Small number of carriers have the energy to get over out of material.
When a bias is applied to the junction either it can make the barrier seem lower from the semiconductor side, or it can make it appear higher.
The bias neither change the barrier height from the metal side.
Finally, this is a Schottky Barrier (rectifying contact), where the junction conducts for one bias polarity, but not the other.
About all metal-semiconductor junctions exhibit some of this rectifying performance.
Schottky Contacts make good diodes and may even be used to make a sympathetic of transistor, but for getting signals into and out of a semiconductor device, we are interested in Ohmic contacts.
Ohmic contacts conduct the same for both polarities (negative and positive). (They follow Ohm's Law).
There are two ways to make a metal-semiconductor contact look ohmic enough to get signals into and out of a semiconductor (or doing the opposite makes a good Schottky contact).
Lower the barrier height
We will use those materials whose barrier height is minor.
Strengthening mayform an alloy between the semiconductor and the metal at the junction, which can also inferior the barrier height.
Make the barrier very narrow
One very interesting property of very tiny particles like electrons and holes is that they can "tunnel" through barriers that they don't have sufficient energy to just pass over.
The probability of tunneling becomes high for very thin barriers .
We make the barrier actual thinnest by doping it very heavily (1019 dopant atoms/cm3 or more).
7) Define Carrier Transport: Generation and Recombination ?
Answer:
Any disturbance of free carriers in a semiconductor form a current( I). This disturbance can be formed by an electric field due to an externally applied voltage(V), since the carriers are charged particles.
This istransfer as carrier drift. In addition, carriers also move from areas high to low carriers.
This carrier transport mechanism is reason by the thermal energy and the associated random motion of the carriers.
We will consider this carriage mechanism as carrier diffusion.
The overall current in a semiconductor generations the addition of the drift and the diffusion current.
After pass electric field to a semiconductor, the electrostatic force causes the carriers to first accelerate and then grasp a constant average velocity, v, due to collisions with impurities and lattice vibrations.
mobility is known as the ratio of the velocity to the practical field .
Diffusion of carriers is obtained by making a carrier density gradient.
Such gradient can be obtained by changing the doping density in a semiconductor or by applying a thermal gradient.
Both carrier transport mechanisms are connected since the same particles and scattering mechanisms are involved.
This leads to a association between the mobility and the diffusion constant called the Einstein relation.
Definition: In the solid-state physics of semiconductors, carrier generation and carrier recombination are developments by which mobile charge carriers (electrons and electron holes) are created and eliminated.
8) What is Semiconductor material of Interest ?
Answer:
Definition : A photo diode is a semiconductor light sensor that makes a voltage(V) or current(I) when light falls on the junction.
It includes an active P-N junction, which is functioned in reverse bias.
When a photon with plenty of energy strikes the semiconductor, an electron or hole pair is created.
The electrons diffuse to the junction to method an electric field.
9) Give one example of Opto electric Device ?
Answer:
Solar Cells:
A solar cell or photo-voltaic cell is an electronic device that directly converts sun’s energy into electricity.
When sunlight falls on a solar cell, it products both a current and a voltage to produce electric power.
Sunlight, which is composed of photons, radiates from the sun.
When photons hit the silicon atoms of the solar cell, they transmission their energy to lose electrons; and then, these high-energy electron flow to an external circuit.
10) Give suitable equation for Density Of States?
Answer:
Joint Density Of States:
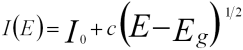for a direct band gap
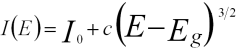for an indirect band gap
Where,
I0 and c -- The constants.
E -- The energy loss
