UNIT 2

1. Explain knowledge base agent

• An intelligent agent needs knowledge about the real world for taking decisions and reasoning to act efficiently.
• Knowledge-based agents are those agents who have the capability of maintaining an internal state of knowledge, reason over that knowledge, update their knowledge after observations and take actions. These agents can represent the world with some formal representation and act intelligently.
• Knowledge-based agents are composed of two main parts:
  • Knowledge-base and
  • Inference system.

A knowledge-based agent must able to do the following:

• An agent should be able to represent states, actions, etc.
• An agent Should be able to incorporate new percepts
• An agent can update the internal representation of the world
• An agent can deduce the internal representation of the world
• An agent can deduce appropriate actions.Knowledge base: Knowledge-base is a central component of a knowledge-based agent, it is also known as KB. It is a collection of sentences (here 'sentence' is a technical term and it is not identical to sentence in English). These sentences are expressed in a language which is called a knowledge representation language. The Knowledge-base of KBA stores fact about the world.

Why use a knowledge base?

Knowledge-base is required for updating knowledge for an agent to learn with experiences and take action as per the knowledge.

Inference system

Inference means deriving new sentences from old. Inference system allows us to add a new sentence to the knowledge base. A sentence is a proposition about the world. Inference system applies logical rules to the KB to deduce new information.

Inference system generates new facts so that an agent can update the KB. An inference system works mainly in two rules which are given as:

• Forward chaining
• Backward chaining

Operations Performed by KBA

Following are three operations which are performed by KBA in order to show the intelligent behavior:

1. TELL: This operation tells the knowledge base what it perceives from the environment.
2. ASK: This operation asks the knowledge base what action it should perform.
3. Perform: It performs the selected action.

A generic knowledge-based agent:

Following is the structure outline of a generic knowledge-based agents program:

1. Function KB-AGENT(percept):  
2. Persistent: KB, a knowledge base   
3.          t, a counter, initially 0, indicating time   
4. TELL(KB, MAKE-PERCEPT-SENTENCE(percept, t))   
5. Action = ASK(KB, MAKE-ACTION-QUERY(t))   
6. TELL(KB, MAKE-ACTION-SENTENCE(action, t))  
7. t = t + 1  
8. Return action   

The knowledge-based agent takes percept as input and returns an action as output. The agent maintains the knowledge base, KB, and it initially has some background knowledge of the real world. It also has a counter to indicate the time for the whole process, and this counter is initialized with zero.

Each time when the function is called, it performs its three operations:

• Firstly it TELLs the KB what it perceives.
• Secondly, it asks KB what action it should take
• Third agent program TELLS the KB that which action was chosen.

The MAKE-PERCEPT-SENTENCE generates a sentence as setting that the agent perceived the given percept at the given time.

The MAKE-ACTION-QUERY generates a sentence to ask which action should be done at the current time.

MAKE-ACTION-SENTENCE generates a sentence which asserts that the chosen action was executed.

2.     Explain various levels and approach of knowledge base agent

Various levels of knowledge-based agent:

A knowledge-based agent can be viewed at different levels which are given below:

1. Knowledge level

Knowledge level is the first level of knowledge-based agent, and in this level, we need to specify what the agent knows, and what the agent goals are. With these specifications, we can fix its behavior. For example, suppose an automated taxi agent needs to go from a station A to station B, and he knows the way from A to B, so this comes at the knowledge level.

2. Logical level:

At this level, we understand that how the knowledge representation of knowledge is stored. At this level, sentences are encoded into different logics. At the logical level, an encoding of knowledge into logical sentences occurs. At the logical level we can expect to the automated taxi agent to reach to the destination B.

3. Implementation level:

This is the physical representation of logic and knowledge. At the implementation level agent perform actions as per logical and knowledge level. At this level, an automated taxi agent actually implement his knowledge and logic so that he can reach to the destination.

Approaches to designing a knowledge-based agent:

There are mainly two approaches to build a knowledge-based agent:

1. 1. Declarative approach: We can create a knowledge-based agent by initializing with an empty knowledge base and telling the agent all the sentences with which we want to start with. This approach is called Declarative approach.
2. 2. Procedural approach: In the procedural approach, we directly encode desired behavior as a program code. Which means we just need to write a program that already encodes the desired behavior or agent.

However, in the real world, a successful agent can be built by combining both declarative and procedural approaches, and declarative knowledge can often be compiled into more efficient procedural code.

3.     Explain propositional logic with example

Propositional logic (PL) is the simplest form of logic where all the statements are made by propositions. A proposition is a declarative statement which is either true or false. It is a technique of knowledge representation in logical and mathematical form.

Example:

1. a) It is Sunday.  
2. b) The Sun rises from West (False proposition)  
3. c) 3+3= 7(False proposition)  
4. d) 5 is a prime number.   

Following are some basic facts about propositional logic:

• Propositional logic is also called Boolean logic as it works on 0 and 1.
• In propositional logic, we use symbolic variables to represent the logic, and we can use any symbol for a representing a proposition, such A, B, C, P, Q, R, etc.
• Propositions can be either true or false, but it cannot be both.
• Propositional logic consists of an object, relations or function, and logical connectives.
• These connectives are also called logical operators.
• The propositions and connectives are the basic elements of the propositional logic.
• Connectives can be said as a logical operator which connects two sentences.
• A proposition formula which is always true is called tautology, and it is also called a valid sentence.
• A proposition formula which is always false is called Contradiction.
• A proposition formula which has both true and false values is called
• Statements which are questions, commands, or opinions are not propositions such as "Where is Rohini", "How are you", "What is your name", are not propositions.

Syntax of propositional logic:

The syntax of propositional logic defines the allowable sentences for the knowledge representation. There are two types of Propositions:

1. Atomic Propositions
2. Compound propositions

• Atomic Proposition: Atomic propositions are the simple propositions. It consists of a single proposition symbol. These are the sentences which must be either true or false.

Example:

1. a) 2+2 is 4, it is an atomic proposition as it is a true fact.  
2. b) "The Sun is cold" is also a proposition as it is a false fact.   

• Compound proposition: Compound propositions are constructed by combining simpler or atomic propositions, using parenthesis and logical connectives.

Example:

1. a) "It is raining today, and street is wet."  
2. b) "Ankit is a doctor, and his clinic is in Mumbai."   

4. Explain Logical Connectives in detail

Logical connectives are used to connect two simpler propositions or representing a sentence logically. We can create compound propositions with the help of logical connectives. There are mainly five connectives, which are given as follows:

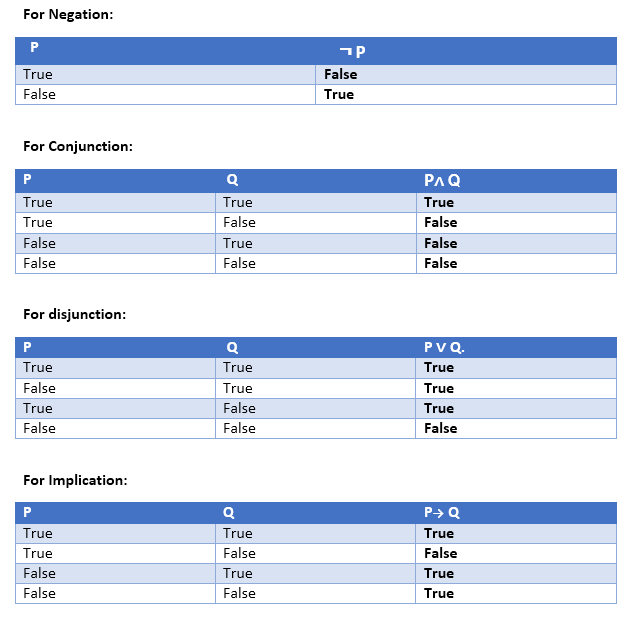
1. Negation: A sentence such as ¬ P is called negation of P. A literal can be either Positive literal or negative literal.
2. Conjunction: A sentence which has ∧ connective such as, P ∧ Q is called a conjunction.
   Example: Rohan is intelligent and hardworking. It can be written as,
   P= Rohan is intelligent,
   Q= Rohan is hardworking. → P∧ Q.
3. Disjunction: A sentence which has ∨ connective, such as P ∨ Q. Is called disjunction, where P and Q are the propositions.
   Example: "Ritika is a doctor or Engineer",
   Here P= Ritika is Doctor. Q= Ritika is Doctor, so we can write it as P ∨ Q.
4. Implication: A sentence such as P → Q, is called an implication. Implications are also known as if-then rules. It can be represented as
               If it is raining, then the street is wet.
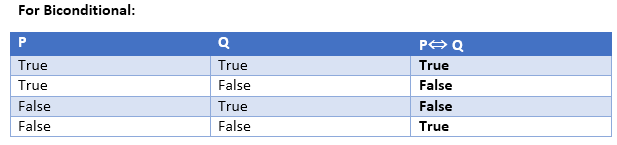
           Let P= It is raining, and Q= Street is wet, so it is represented as P → Q
5. Biconditional: A sentence such as P⇔ Q is a Biconditional sentence, example If I am breathing, then I am alive
               P= I am breathing, Q= I am alive, it can be represented as P ⇔ Q.

Following is the summarized table for Propositional Logic Connectives:

Truth Table:

In propositional logic, we need to know the truth values of propositions in all possible scenarios. We can combine all the possible combination with logical connectives, and the representation of these combinations in a tabular format is called Truth table. Following are the truth table for all logical connectives:

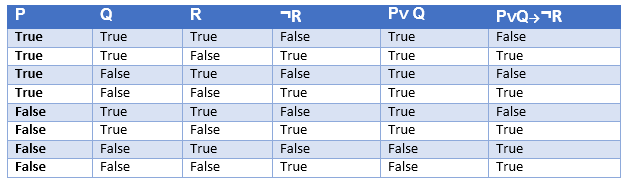
Truth table with three propositions:

We can build a proposition composing three propositions P, Q, and R. This truth table is made-up of 8n Tuples as we have taken three proposition symbols.

Precedence of connectives:

Just like arithmetic operators, there is a precedence order for propositional connectors or logical operators. This order should be followed while evaluating a propositional problem. Following is the list of the precedence order for operators:

Note: For better understanding use parenthesis to make sure of the correct interpretations. Such as ¬R∨ Q, It can be interpreted as (¬R) ∨ Q.

5.     Explain First-Order logic in detail with some examples

• First-order logic is another way of knowledge representation in artificial intelligence. It is an extension to propositional logic.
• FOL is sufficiently expressive to represent the natural language statements in a concise way.
• First-order logic is also known as Predicate logic or First-order predicate logic. First-order logic is a powerful language that develops information about the objects in a more easy way and can also express the relationship between those objects.
• First-order logic (like natural language) does not only assume that the world contains facts like propositional logic but also assumes the following things in the world:
  • Objects: A, B, people, numbers, colors, wars, theories, squares, pits, wumpus, ......
  • Relations: It can be unary relation such as: red, round, is adjacent, or n-any relation such as: the sister of, brother of, has color, comes between
  • Function: Father of, best friend, third inning of, end of, ......
• As a natural language, first-order logic also has two main parts:
  1. Syntax
  2. Semantics

Syntax of First-Order logic:

The syntax of FOL determines which collection of symbols is a logical expression in first-order logic. The basic syntactic elements of first-order logic are symbols. We write statements in short-hand notation in FOL.

Basic Elements of First-order logic:

Following are the basic elements of FOL syntax:

Atomic sentences:

• Atomic sentences are the most basic sentences of first-order logic. These sentences are formed from a predicate symbol followed by a parenthesis with a sequence of terms.
• We can represent atomic sentences as Predicate (term1, term2, ......, term n).

Example: Ravi and Ajay are brothers: => Brothers(Ravi, Ajay).
                Chinky is a cat: => cat (Chinky).

Complex Sentences:

• Complex sentences are made by combining atomic sentences using connectives.

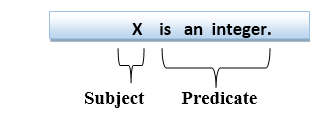
First-order logic statements can be divided into two parts:

• Subject: Subject is the main part of the statement.
• Predicate: A predicate can be defined as a relation, which binds two atoms together in a statement.

Consider the statement: "x is an integer.", it consists of two parts, the first part x is the subject of the statement and second part "is an integer," is known as a predicate.

Quantifiers in First-order logic:

• A quantifier is a language element which generates quantification, and quantification specifies the quantity of specimen in the universe of discourse.
• These are the symbols that permit to determine or identify the range and scope of the variable in the logical expression. There are two types of quantifier:
  1. Universal Quantifier, (for all, everyone, everything)
  2. Existential quantifier, (for some, at least one).

Universal Quantifier:

Universal quantifier is a symbol of logical representation, which specifies that the statement within its range is true for everything or every instance of a particular thing.

The Universal quantifier is represented by a symbol ∀, which resembles an inverted A.

Note: In universal quantifier we use implication "→".

If x is a variable, then ∀x is read as:

• For all x
• For each x
• For every x.

Existential Quantifier:

Existential quantifiers are the type of quantifiers, which express that the statement within its scope is true for at least one instance of something.

It is denoted by the logical operator ∃, which resembles as inverted E. When it is used with a predicate variable then it is called as an existential quantifier.

Note: In Existential quantifier we always use AND or Conjunction symbol (∧).

If x is a variable, then existential quantifier will be ∃x or ∃(x). And it will be read as:

• There exists a 'x.'
• For some 'x.'
• For at least one 'x.'

Points to remember:

• The main connective for universal quantifier ∀ is implication →.
• The main connective for existential quantifier ∃ is and ∧.

Properties of Quantifiers:

• In universal quantifier, ∀x∀y is similar to ∀y∀x.
• In Existential quantifier, ∃x∃y is similar to ∃y∃x.
• ∃x∀y is not similar to ∀y∃x.

Some Examples of FOL using quantifier:

1. All birds fly.
In this question the predicate is "fly(bird)."
And since there are all birds who fly so it will be represented as follows.
              ∀x bird(x) →fly(x).

2. Every man respects his parent.
In this question, the predicate is "respect(x, y)," where x=man, and y= parent.
Since there is every man so will use ∀, and it will be represented as follows:
              ∀x man(x) → respects (x, parent).

3. Some boys play cricket.
In this question, the predicate is "play(x, y)," where x= boys, and y= game. Since there are some boys so we will use ∃, and it will be represented as:
              ∃x boys(x) → play(x, cricket).

4. Not all students like both Mathematics and Science.
In this question, the predicate is "like(x, y)," where x= student, and y= subject.
Since there are not all students, so we will use ∀ with negation, so following representation for this:
              ¬∀ (x) [ student(x) → like(x, Mathematics) ∧ like(x, Science)].

5. Only one student failed in Mathematics.
In this question, the predicate is "failed(x, y)," where x= student, and y= subject.
Since there is only one student who failed in Mathematics, so we will use following representation for this:
              ∃(x) [ student(x) → failed (x, Mathematics) ∧∀ (y) [¬(x==y) ∧ student(y) → ¬failed (x, Mathematics)].

Free and Bound Variables:

The quantifiers interact with variables which appear in a suitable way. There are two types of variables in First-order logic which are given below:

Free Variable: A variable is said to be a free variable in a formula if it occurs outside the scope of the quantifier.

Example: ∀x ∃(y)[P (x, y, z)], where z is a free variable.

Bound Variable: A variable is said to be a bound variable in a formula if it occurs within the scope of the quantifier.

6.     Explain Inference in first order logic with examples

Inference in First-Order Logic is used to deduce new facts or sentences from existing sentences. Before understanding the FOL inference rule, let's understand some basic terminologies used in FOL.

Substitution:

Substitution is a fundamental operation performed on terms and formulas. It occurs in all inference systems in first-order logic. The substitution is complex in the presence of quantifiers in FOL. If we write F[a/x], so it refers to substitute a constant "a" in place of variable "x".

Note: First-order logic is capable of expressing facts about some or all objects in the universe.

Equality:

First-Order logic does not only use predicate and terms for making atomic sentences but also uses another way, which is equality in FOL. For this, we can use equality symbols which specify that the two terms refer to the same object.

Example: Brother (John) = Smith.

As in the above example, the object referred by the Brother (John) is similar to the object referred by Smith. The equality symbol can also be used with negation to represent that two terms are not the same objects.

Example: ￢(x=y) which is equivalent to x ≠y.

FOL inference rules for quantifier:

As propositional logic we also have inference rules in first-order logic, so following are some basic inference rules in FOL:

• Universal Generalization
• Universal Instantiation
• Existential Instantiation
• Existential introduction

1. Universal Generalization:

• Universal generalization is a valid inference rule which states that if premise P(c) is true for any arbitrary element c in the universe of discourse, then we can have a conclusion as ∀ x P(x).
• It can be represented as: .
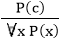• This rule can be used if we want to show that every element has a similar property.
• In this rule, x must not appear as a free variable.

Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true.

2. Universal Instantiation:

• Universal instantiation is also called as universal elimination or UI is a valid inference rule. It can be applied multiple times to add new sentences.
• The new KB is logically equivalent to the previous KB.
• As per UI, we can infer any sentence obtained by substituting a ground term for the variable.
• The UI rule state that we can infer any sentence P(c) by substituting a ground term c (a constant within domain x) from ∀ x P(x) for any object in the universe of discourse.
• It can be represented as:.

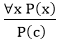Example:1.

IF "Every person like ice-cream"=> ∀x P(x) so we can infer that
"John likes ice-cream" => P(c)

Example: 2.

Let's take a famous example,

"All kings who are greedy are Evil." So let our knowledge base contains this detail as in the form of FOL:

∀x king(x) ∧ greedy (x) → Evil (x),

So from this information, we can infer any of the following statements using Universal Instantiation:

• King(John) ∧ Greedy (John) → Evil (John),
• King(Richard) ∧ Greedy (Richard) → Evil (Richard),
• King(Father(John)) ∧ Greedy (Father(John)) → Evil (Father(John)),

3. Existential Instantiation:

• Existential instantiation is also called as Existential Elimination, which is a valid inference rule in first-order logic.
• It can be applied only once to replace the existential sentence.
• The new KB is not logically equivalent to old KB, but it will be satisfiable if old KB was satisfiable.
• This rule states that one can infer P(c) from the formula given in the form of ∃x P(x) for a new constant symbol c.
• The restriction with this rule is that c used in the rule must be a new term for which P(c ) is true.
• It can be represented as:

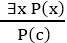
Example:

From the given sentence: ∃x Crown(x) ∧ OnHead(x, John),

So we can infer: Crown(K) ∧ OnHead( K, John), as long as K does not appear in the knowledge base.

• The above used K is a constant symbol, which is called Skolem constant.
• The Existential instantiation is a special case of Skolemization process.

4. Existential introduction

• An existential introduction is also known as an existential generalization, which is a valid inference rule in first-order logic.
• This rule states that if there is some element c in the universe of discourse which has a property P, then we can infer that there exists something in the universe which has the property P.
• It can be represented as:
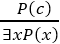
• Example: Let's say that,
  "Priyanka got good marks in English."
  "Therefore, someone got good marks in English."

7.     What is Generalized Modus Ponens Rule?

For the inference process in FOL, we have a single inference rule which is called Generalized Modus Ponens. It is lifted version of Modus ponens.

Generalized Modus Ponens can be summarized as, " P implies Q and P is asserted to be true, therefore Q must be True."

According to Modus Ponens, for atomic sentences pi, pi', q. Where there is a substitution θ such that SUBST (θ, pi',) = SUBST(θ, pi), it can be represented as:

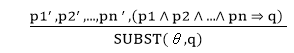
Example:

We will use this rule for Kings are evil, so we will find some x such that x is king, and x is greedy so we can infer that x is evil.

1. Here let say, p1' is king(John)        p1 is king(x)  
2. p2' is Greedy(y)                       p2 is Greedy(x)  
3. θ is {x/John, y/John}                  q is evil(x)  

SUBST(θ,q).      

8.     Explain Resolution with examples

Resolution is a theorem proving technique that proceeds by building refutation proofs, i.e., proofs by contradictions. It was invented by a Mathematician John Alan Robinson in the year 1965.

Resolution is used, if there are various statements are given, and we need to prove a conclusion of those statements. Unification is a key concept in proofs by resolutions. Resolution is a single inference rule which can efficiently operate on the conjunctive normal form or clausal form.

Clause: Disjunction of literals (an atomic sentence) is called a clause. It is also known as a unit clause.

Conjunctive Normal Form: A sentence represented as a conjunction of clauses is said to be conjunctive normal form or CNF.

Note: To better understand this topic, firstly learns the FOL in AI.

The resolution inference rule:

The resolution rule for first-order logic is simply a lifted version of the propositional rule. Resolution can resolve two clauses if they contain complementary literals, which are assumed to be standardized apart so that they share no variables.

Where li and mj are complementary literals.

This rule is also called the binary resolution rule because it only resolves exactly two literals.

Example:

We can resolve two clauses which are given below:

[Animal (g(x) V Loves (f(x), x)]       and       [￢ Loves(a, b) V ￢Kills(a, b)]

Where two complimentary literals are: Loves (f(x), x) and ￢ Loves (a, b)

These literals can be unified with unifier θ= [a/f(x), and b/x] , and it will generate a resolvent clause:

[Animal (g(x) V ￢ Kills(f(x), x)].

Steps for Resolution:

1. Conversion of facts into first-order logic.
2. Convert FOL statements into CNF
3. Negate the statement which needs to prove (proof by contradiction)
4. Draw resolution graph (unification).

To better understand all the above steps, we will take an example in which we will apply resolution.

Example:

1. John likes all kind of food.
2. Apple and vegetable are food
3. Anything anyone eats and not killed is food.
4. Anil eats peanuts and still alive
5. Harry eats everything that Anil eats.
   Prove by resolution that:
6. John likes peanuts.

9.     Explain in detail steps involved in resolution

Step-1: Conversion of Facts into FOL

In the first step we will convert all the given statements into its first order logic.

Step-2: Conversion of FOL into CNF

In First order logic resolution, it is required to convert the FOL into CNF as CNF form makes easier for resolution proofs.

• Eliminate all implication (→) and rewrite
  1. ∀x ¬ food(x) V likes(John, x)
  2. Food(Apple) Λ food(vegetables)
  3. ∀x ∀y ¬ [eats(x, y) Λ ¬ killed(x)] V food(y)
  4. Eats (Anil, Peanuts) Λ alive(Anil)
  5. ∀x ¬ eats(Anil, x) V eats(Harry, x)
  6. ∀x¬ [¬ killed(x) ] V alive(x)
  7. ∀x ¬ alive(x) V ¬ killed(x)
  8. Likes(John, Peanuts).
• Move negation (¬)inwards and rewrite
  1. ∀x ¬ food(x) V likes(John, x)
  2. Food(Apple) Λ food(vegetables)
  3. ∀x ∀y ¬ eats(x, y) V killed(x) V food(y)
  4. Eats (Anil, Peanuts) Λ alive(Anil)
  5. ∀x ¬ eats(Anil, x) V eats(Harry, x)
  6. ∀x ¬killed(x) ] V alive(x)
  7. ∀x ¬ alive(x) V ¬ killed(x)
  8. Likes(John, Peanuts).
• Rename variables or standardize variables
  1. ∀x ¬ food(x) V likes(John, x)
  2. Food(Apple) Λ food(vegetables)
  3. ∀y ∀z ¬ eats(y, z) V killed(y) V food(z)
  4. Eats (Anil, Peanuts) Λ alive(Anil)
  5. ∀w¬ eats(Anil, w) V eats(Harry, w)
  6. ∀g ¬killed(g) ] V alive(g)
  7. ∀k ¬ alive(k) V ¬ killed(k)
  8. Likes(John, Peanuts).
• Eliminate existential instantiation quantifier by elimination.
  In this step, we will eliminate existential quantifier ∃, and this process is known as Skolemization. But in this example problem since there is no existential quantifier so all the statements will remain same in this step.
• Drop Universal quantifiers.
  In this step we will drop all universal quantifier since all the statements are not implicitly quantified so we don't need it.
  1. ¬ food(x) V likes(John, x)
  2. Food(Apple)
  3. Food(vegetables)
  4. ¬ eats(y, z) V killed(y) V food(z)
  5. Eats (Anil, Peanuts)
  6. Alive(Anil)
  7. ¬ eats(Anil, w) V eats(Harry, w)
  8. Killed(g) V alive(g)
  9. ¬ alive(k) V ¬ killed(k)
  10. Likes(John, Peanuts).

Note: Statements "food(Apple) Λ food(vegetables)" and "eats (Anil, Peanuts) Λ alive(Anil)" can be written in two separate statements.

• Distribute conjunction ∧ over disjunction ¬.
  This step will not make any change in this problem.

Step-3: Negate the statement to be proved

In this statement, we will apply negation to the conclusion statements, which will be written as ¬likes(John, Peanuts)

Step-4: Draw Resolution graph:

Now in this step, we will solve the problem by resolution tree using substitution. For the above problem, it will be given as follows:

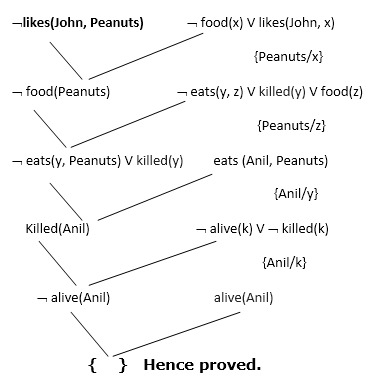
Hence the negation of the conclusion has been proved as a complete contradiction with the given set of statements.

Explanation of Resolution graph:

• In the first step of resolution graph, ¬likes(John, Peanuts) , and likes(John, x) get resolved(canceled) by substitution of {Peanuts/x}, and we are left with ¬ food(Peanuts)
• In the second step of the resolution graph, ¬ food(Peanuts) , and food(z) get resolved (canceled) by substitution of { Peanuts/z}, and we are left with ¬ eats(y, Peanuts) V killed(y) .
• In the third step of the resolution graph, ¬ eats(y, Peanuts) and eats (Anil, Peanuts) get resolved by substitution {Anil/y}, and we are left with Killed(Anil) .
• In the fourth step of the resolution graph, Killed(Anil) and ¬ killed(k) get resolve by substitution {Anil/k}, and we are left with ¬ alive(Anil) .
• In the last step of the resolution graph ¬ alive(Anil) and alive(Anil) get resolved.

10. What is theorem proving explain in detail with examples?

Reasoning by theorem proving is a weak method, compared to experts systems, because it does not make use of domain knowledge. This, on the other hand, may be a strength, if no domain heuristics are available (reasoning from first principles). Theorem proving is usually limited to sound reasoning.

Differentiate between

• Theorem provers: fully automatic
• Proof assistants: require steps as input, take care of bookkeeping and sometimes 'easy' proofs.

Theorem proving requires

• a logic (syntax)
• a set of axioms and inference rules
• a strategy on when how to search through the possible applications of the axioms and rules

Examples of axioms
p -> (q->p)
(p->(q->r)) -> ((p->q) ->(p->r))
p \/ ~p
p->(~p->q)
Notation: I use ~ for "not", since it's on my keyboard.

Examples of inference rules
 

Strategies
forwards - start from axioms, apply rules
backwards - start from the theorem (in general: a set of goals), work backwards to the axioms

Depth-first or breadth-first

When to apply which rule

General questions:
are the rules correct (sound)?
is there a proof for every logical consequence (complete)?
can we remove rules (redundant)?
Having redundant rules may allow shorter proofs, but a larger search space.

Resolution and refutation

We want to prove theory -> goal.
The theory is usually a set of facts and rules, that can be treated as axioms (by the rule called implication above). A theory is usually quite stable, and used to prove various goals.

• We use contradiction, add ~goal to the axioms, and try to prove false.
• The theory and ~goal are put in clausal form - a set (conjunction) of  clauses
  [see Luger p 558-560]
• Use resolution and unification to derive false

Clauses
a clause is a universially quantified disjunction of literals
a literal is an atomic formula or its negation
examples of clauses: p \/ q, p(X) \/ q(Y), ~p(X) \/ q(X).
A special case is Horn-clauses: they have at most one positive (not negated) literal.
Three subclasses:
facts (1 pos, 0 neg): p(a,b).
rules (1 pos, > 0 neg): ~p \/ ~q \/ r - often written as: p /\ q -> r
goals(0 pos): ~p \/ ~q - if we want to prove p/\q from the theory, we add this clause - can be written as p /\ q -> false

Skolemization (p. 559)
How to remove existential quantification? Use function symbols!
Example: every person has a mother: (for all X) person(X) -> (exists Y) mother(X,Y)
Give a name to Y: the mother of X. (for all X) person(X) -> mother(X,mother_of(X))

This allows us to define datastructures in the logic.
Example: if X is an element and Y a list, then there is a list with head X and tail Y.
(for all X,Y) elt(X) /\ list(Y) -> (exists Z) list(Z) /\ head(Z,X) /\ tail(Z,Y)
first we name Z the cons of X and Y, then we get 3 rules:
elt(X) /\ list(Y) -> list(cons(X,Y)).
elt(X) /\ list(Y) -> head(cons(X,Y), X).
elt(X) /\ list(Y) -> tail(cons(X,Y), Y).

Unification

Unification (2.3.2) is used to perform instantiation before (during) resolution.

Simple case:
Resolve list(nil) with ~elt(X) \/ ~list(Y) \/ list(cons(X,Y)).
First we must instantiate Y to nil, then we can derive ~elt(X) \/ list(cons(X,nil)).

Hard case:
I want to prove that there is a list that has the head mother_of(john).
So I take as a goal its negation ~(exists X)(list(X) /\ head(X,mother_of(john)))
This gives the clause  ~list(X) \/ ~head(X,mother_of(john))
We can resolve with ~elt(X) \/ ~list(Y) \/ head(cons(X,Y),X).
Problem 1: the X's in both clauses "accidentally" have the same name.
Solution 1: rename to ~elt(Z) \/ ~list(Y) \/ head(cons(Z,Y),Z).
Problem 2: what is the common instance of head(cons(Z,Y),Z) and head(X,mother_of(john))?
Answer - the result of unification: head(cons(mother_of(john),Y),mother_of(john))
The unifier is: {Z/mother_of(john), X/cons(mother_of(john),Y)}
The resolvent (resulting clause) is
(~list(X) \/ ~elt(Z) \/ ~list(Y)){Z/mother_of(john), X/cons(mother_of(john),Y)} =
~list(cons(mother_of(john),Y)) \/ ~elt(mother_of(john)) \/ ~list(Y)

Exercise: use the first list-rule and the facts elt(mother_of(john)) and list(nil)to complete the proof.

Unification as rewriting
the algorithm maintains a set of equalities. Each time, remove an equality and apply the applicable  rule.

• Var1 = Var1 - nothing (just remove the equality)
• Var1 = Expr - in all other equalities, replace Var1 by Expr, keep Var1 = Expr
  exception: if Var1 occurs in Expr, then FAIL
• f(A1,..,An) = f(B1,..,Bn) - add {A1 = B1, .., An = Bn}
• f(A1,..,An) = g(B1,..,Bm) - FAIL

Example (the equality selected is underlined)
{head(cons(Z,Y),Z) = head(X,mother_of(john))} - use the first f-rule, f=head, n=2.
{cons(Z,Y) = X, Z = mother_of(john)}
{cons(mother_of(john),Y) = X, Z = mother_of(john)}
no more applicable rules, and no FAIL, so we have a unifier.

Resolution and Prolog

A Prolog program consists of Horn-clauses: facts and rules.
We give the program a goal, which it turns into a Horn clause with only negative literals.
Prolog uses linear resolution:
it takes the goal and a rule/fact, and produces a new goal, until it derives false. This proves the goal.
(Other outcomes are that Prolog runs out of options and cannot prove the goal, or that it goes into an infinite loop.)
Linear resolution is not complete for predicate logic in general, but it is complete in this special case.
Prolog uses depth-first search in a search tree - choices arise when more than one rule is applicable.