undefined | unit 1 introduction

FLAT

UNIT 1

Explain Context Free Grammars

Simplifying Context Free Grammars

A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production rules satisfy one of the following conditions:

A non-terminal generating a terminal (e.g.; X->x)

A non-terminal generating two non-terminals (e.g.; X->YZ)

Start symbol generating ε. (e.g.; S->ε)

Consider the following grammars,

G1 = {S->a, S->AZ, A->a, Z->z}

G2 = {S->a, S->aZ, Z->a}

The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.

Note –

CNF is a pre-processing step used in various algorithms.

For generation of string x of length ‘m’, it requires ‘2m-1’ production or steps in CNF.

2. How to convert CFG to CNF?

Step 1. Remove start from RHS. If start symbol S is at the RHS of any production in the grammar, create a new production as:S0->S where S0 is the new start symbol.

Step 2. Remove null, unit and useless productions. If CFG comprises of any production rules, remove them.

Step 3. Remove terminals from RHS. For eg; production rule X->xY can be decomposed as: X->ZY Z->x

Step 4. Remove RHS with more than two non-terminals. e.g,; production rule X->XYZ can be decomposed as:
X->PZ
P->XY

3. Explain Regular expressions and languages

A Regular Expression can be recursively defined as follows −

ε is a Regular Expression indicates the language containing an empty string. (L (ε) = {ε})

φ is a Regular Expression denoting an empty language. (L (φ) = { })

x is a Regular Expression where L = {x}

If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then

X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).
X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)
R* is a Regular Expression corresponding to the language L(R*) where L(R*) = (L(R))*

If we apply any of the rules several times from 1 to 5, they are Regular Expressions.

UNIX Operator Extensions

Regular expressions are used frequently in Unix:

In the command line

Within text editors

In the context of pattern matching programs such as grep and egrep

Additional operators are recognized by unix. These operators are used for convenience only.

character classes: '[' <list of chars> ']'

start of a line: '^'

end of a line: '$'

Wildcard matching any character except newline: '.'

Optional instance: R? = epsilon | R

one or more instances: R+ == RR*

4. What is Deterministic finite automata (DFA) and equivalence with regular expressions?

In DFA, for each input symbol, one can determine the state to which the machine will move. Hence, it is called Deterministic Automaton. As it has a finite number of states, the machine is called Deterministic Finite Machine or Deterministic Finite Automaton.

An automaton can be represented by a 5-tuple (Q, ∑, δ, q0, F), where −

Q is a finite set of states.

∑ is a finite set of symbols, called the alphabet of the automaton.

δ is the transition function.

q0 is the initial state from where any input is processed (q0 ∈ Q).

F is a set of final state/states of Q (F ⊆ Q).

A Review (supplemental)

Recall the example of designing a vending machine selling 20-dolllar food packs in Figure 1.3.2.What abstract concepts are involved in the design?  See the definition next.

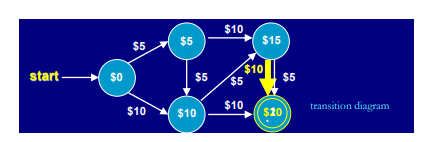
Figure Recall the example

Advantages and disadvantages

DFAs were invented to model of a Turing machine, which was too general to study properties of real world machines.

DFAs are one of the most practical models of computation, since there is a trivial linear time, constant-space, online algorithm there are efficient algorithms to find a DFA recognizing:

The union/intersection of the languages recognized by two given DFAs.

The complement of the language recognized by a given DFA.

On the other hand, finite state automata are of strictly limited power in the languages they can recognize; many simple languages, including any problem that requires more than constant space to solve, cannot be recognized by a DFA. • The classical example of a simply described language that no DFA can recognize is bracket language, i.e., language that consists of properly paired brackets such as word "(( )( ))".

5. What is Non deterministic finite automata (NFA) and equivalence with DFA?

In NDFA, for a particular input symbol, the machine can move to any combination of the states in the machine. In other words, the exact state to which the machine moves cannot be determined. Hence, it is called Non-deterministic Automaton. As it has finite number of states, the machine is called Non-deterministic Finite Machine or Non-

deterministic Finite Automaton.

Q → Finite non-empty set of states.
∑ → Finite non-empty set of input symbols.
∂ → Transitional Function.
q0 → Beginning state.
F → Final State

Review of a previous example of DFA

Original version --- see Fig. (the same as Fig.)

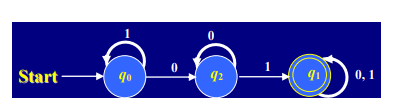
Figure Step 1 For NDFA Example

A nondeterministic finite automaton (NFA) version of the above DFA --- see Fig. 2.

More intuitive!

How to design an NFA will be described later.

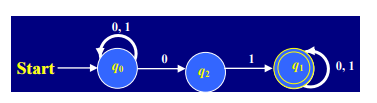
Figure Step 1 For NDFA Example

Some properties of NFA’s (see Fig. 2.6 for the illustration) ---

Some transitions may “die,” like ˆ  (q2, 0).

Some transitions have multiple choices, like ˆ  (q0, 0) = q0 and q2.

Example --- Design an NFA accepting the following language L = {w | w{0, 1}* and ends in 01}.

6. DFA vs NDFA

The following table lists the differences between DFA and NDFA.

DFA	NDFA
The transition from a state is to a single particular next state for each input symbol. Hence it is called deterministic.	The transition from a state can be to multiple next states for each input symbol. Hence it is called non-deterministic.
Empty string transitions are not seen in DFA.	NDFA permits empty string transitions.
Backtracking is allowed in DFA	In NDFA, backtracking is not always possible.
Requires more space.	Requires less space.
A string is accepted by a DFA, if it transits to a final state.	A string is accepted by a NDFA, if at least one of all possible transitions ends in a final state.

7. Explain Regular grammars and equivalence with finite automata

Regular expressions and finite automata have equivalent expressive power:

For every regular expression R, there is a corresponding FA that accepts the set of strings generated by R.

For every FA A there is a corresponding regular expression that generates the set of strings accepted by A.

The proof is in two parts:

an algorithm that, given a regular expression R, produces an FA A such that L(A) == L(R).

an algorithm that, given an FA A, produces a regular expression R such that L(R) == L(A).

Our construction of FA from regular expressions will allow "epsilon transitions" (a transition from one state to another with epsilon as the label). Such a transition is always possible, since epsilon (or the empty string) can be said to exist between any two input symbols. We can show that such epsilon transitions are a notational convenience; for every FA with epsilon transitions there is a corresponding FA without them.

Constructing an FA from an RE

We begin by showing how to construct an FA for the operands in a regular expression.

If the operand is a character c, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and a transition from s0 to sF with label c.

If the operand is epsilon, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and an epsilon transition from s0 to sF.

If the operand is null, then our FA has two states, s0 (the start state) and sF (the final, accepting state), and no transitions.

Given FA for R1 and R2, we now show how to build an FA for R1R2, R1|R2, and R1*. Let A (with start state a0 and final state aF) be the machine accepting L(R1) and B (with start state b0 and final state bF) be the machine accepting L(R2).

The machine C accepting L(R1R2) includes A and B, with start state a0, final state bF, and an epsilon transition from aF to b0.

The machine C accepting L(R1|R2) includes A and B, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and b0, and from aF and bF to cF.

The machine C accepting L(R1*) includes A, with a new start state c0, a new final state cF, and epsilon transitions from c0 to a0 and cF, and from aF to a0, and from aF to cF.

Eliminating Epsilon Transitions

If epsilon transitions can be eliminated from an FA, then construction of an FA from a regular expression can be completed.

Epsilon transitions offers a choice: It allows us to stay in a state or move to a new state, regardless of the input symbol.

If starting in state s1, state s2 can be reached via a series of epsilon transitions followed by a transition on input symbol x, replacement of the epsilon transitions with a single transition from s1 to s2 on symbol x.

Algorithm for Eliminating Epsilon Transitions

A finite automaton F2 can be build with no epsilon transitions from a finite automaton F1 as follows:

The states of F2 are all the states of F1 that have an entering transition labeled by some symbol other than epsilon, plus the start state of F1, which is also the start state of F2.

For each state in F1, determine which other states are reachable via epsilon transitions only. If a state of F1 can reach a final state in F1 via epsilon transitions, then the corresponding state is a final state in F2.

For each pair of states i and j in F2, there is a transition from state i to state j on input x if there exists a state k that is reachable from state i via epsilon transitions in F1, and there is a transition in F1 from state k to state j on input x.

8. Write some Properties of regular languages

Regular languages are closed under a wide variety of operations.

Union and intersection

Pick DFAs recognizing the two languages and use the cross-product construction to build a DFA recognizing their union or intersection. See Sipser Theorem 1.25. Also see Sipser 1.45 for another way to do union.

Set complement

Pick a DFA recognizing the language, then swap the accept/non-accept markings on its states.

String reversal

Pick an NFA recognizing the language. Create a new final state, with epsilon transitions to it from all the old final states. Then swap the final and start states and reverse all the transition arrows.

Set difference

Re-write set difference using a combination of intersection and set complement

Concatenation and Star

Pick an NFA recognizing the language and modify it as described in Sipser Theorems 1.47 and 1.49

Homomorphism

A homomorphism is a function from strings to strings. What makes it a homomorphism is that its output on a multi-character string is just the concatenation of its outputs on each individual character in the string. Or, equivalently, h(xy) = h(x)h(y) for any strings x and y. If S is a set of strings, then h(S) is {w : w = h(x) for some x in S}.

To show that regular languages are closed under homomorphism, choose an arbitrary regular language L and a homomorphism h. It can be represented using a regular expression R. But then h(R) is a regular expression representing h(L). So h(L) must also be regular.

Notice that regular languages are not closed under the subset/superset relation. For example, 0*1* is regular, but its subset {On1n : n >= 0} is not regular, but its subset {01, 0011, 000111} is regular again.

9. What is Pumping lemma for regular languages, minimization of finite automata?

Lemma: The language 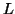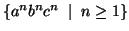$L$ = $\{a^nb^nc^n\; \mid\; n \geq 1\}$ is not context free.

Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let 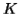$K$ be the constant of the Pumping Lemma.
Considering the string 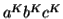$a^Kb^Kc^K$ , where 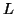$L$ is length greater than $K$ .
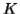By the Pumping Lemma this is represented as 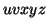$uvxyz$ , such that all 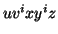$uv^ixy^iz$ are also in 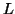$L$ , which is not possible, as:

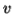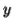either $v$ or $y$ cannot contain many letters from 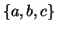$\{a,b,c\}$ ; else they are in the wrong order .

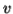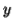if $v$ or $y$ consists of a's, b's or c's, then 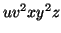$uv^2xy^2z$ cannot maintain the balance amongst the three letters.

Lemma: The language 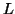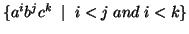$L$ = $\{a^ib^jc^k\; \mid\; i < j\; and\; i < k\}$ is not context free.

Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.

Let 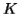$K$ be the constant of the Pumping Lemma.
Considering the string 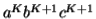$a^Kb^{K+1}c^{K+1}$ , which is $L$ > $K$ .
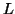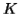By the Pumping Lemma this must be represented as 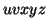$uvxyz$ , such that all 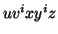$uv^ixy^iz$ are also in $L$ .

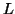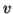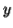-As mentioned previously neither $v$ nor $y$ may contain a mixture of symbols.

-Suppose 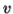$v$ consists of a's.
Then there is no way 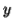$y$ cannot have b's and c's. It generate enough letters to keep them more than that of the a's (it can do it for one or the other of them, not both).
Similarly 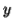$y$ cannot consist of just a's.

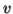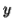-So suppose then that $v$ or $y$ contains only b's or only c's.
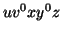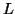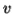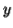Consider the string $uv^0xy^0z$ which must be in $L$ . Since we have dropped both $v$ and $y$ , we must have at least one b' or one c' less than we had in 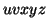$uvxyz$ , which was 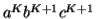$a^Kb^{K+1}c^{K+1}$ . Consequently, this string no longer has enough of either b's or c's to be a member of $L$ .

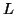10. Define: (i) Finite Automaton(FA) (ii)Transition diagram

FA consists of a finite set of states and a set of transitions from state to state that occur on input symbols chosen from an alphabet ∑. Finite Automaton is denoted by a

5- tuple(Q,∑,δ,q0,F), where Q is the finite set of states , ∑ is a finite input alphabet, q0 in

Q is the initial state, F is the set of final states and δ is the transition mapping function

Q * Σ to Q.

Transition diagram is a directed graph in which the vertices of the graph correspond to the states of FA. If there is a transition from state q to state p on input a, then there is an arc labeled ‘ a ‘ from q to p in the transition diagram.

Sign Up