UNIT 2
CFLs are used by the compiler in the parsing phase as they define the syntax of a programming language and are used in many editors.
There are four important components in a grammatical description of a language:
- A variable that is being defined by the production. This variable is often called the head of the production.
- The production symbol ->.
- A string of zero or more terminals and variable.
Formal definition
A context-free grammar (CFG) is a 4-tuple G=(Vn, Vt, S, P), where Vn and Vt are disjoint finite sets, S is an element of Vn, and P is a finite set of formulas of the form A -> α, where A ϵ Vn and α ϵ (Vn U Vt)*.
2. What is Chomsky normal forms?
A context free grammar (CFG) is in Chomsky Normal Form (CNF) if all production rules satisfy one of the following conditions:
Consider the following grammars,
G1 = {S->a, S->AZ, A->a, Z->z}
G2 = {S->a, S->aZ, Z->a}
The grammar G1 is in CNF as production rules satisfy the rules specified for CNF. However, the grammar G2 is not in CNF as the production rule S->aZ contains terminal followed by non-terminal which does not satisfy the rules specified for CNF.
Note –
3. What is Greibach normal forms?
A CFG is in Greibach Normal Form if the Productions are in the following forms −
A → b
A → bD1…Dn
S → ε
where A, D1,....,Dn are non-terminals and b is a terminal.
Algorithm to Convert a CFG into Greibach Normal Form
Step 1 − If the start symbol S occurs on some right side, create a new start symbol S’ and a new production S’ → S.
Step 2 − Remove Null productions. (Using the Null production removal algorithm discussed earlier)
Step 3 − Remove unit productions. (Using the Unit production removal algorithm discussed earlier)
Step 4 − Remove all direct and indirect left-recursion.
Step 5 − Do proper substitutions of productions to convert it into the proper form of GNF.
4. Problem
Convert the following CFG into CNF
S → XY | Xn | p
X → mX | m
Y → Xn | o
Solution
Here, S does not appear on the right side of any production and there are no unit or null productions in the production rule set. So, we can skip Step 1 to Step 3.
Step 4
Now after replacing
X in S → XY | Xo | p
with
mX | m
we obtain
S → mXY | mY | mXo | mo | p.
And after replacing
X in Y → Xn | o
with the right side of
X → mX | m
we obtain
Y → mXn | mn | o.
Two new productions O → o and P → p are added to the production set and then we came to the final GNF as the following −
S → mXY | mY | mXC | mC | p
X → mX | m
Y → mXD | mD | o
O → o
P → p
5. Explain Parse trees
Figure Parse trees
A parse tree is an entity which represents the structure of the derivation of a terminal string from some non-terminal. Key features to define are the root ∈ V and yield ∈ Σ* of each tree.
Here, parse trees are constructed from bottom up, not top down.
The actual construction of "adding children" should be made more precise, but we intuitively know what's going on.
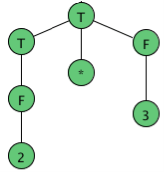
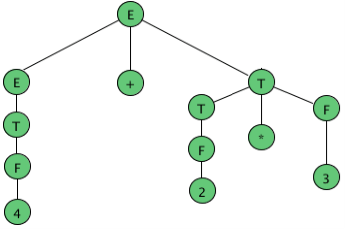
As an example, here are all the parse (sub) trees used to build the parse tree for the arithmetic expression 4 + 2 * 3 using the expression grammar
E → E + T | E - T | T
T → T * F | F
F → a | ( E )
where a represents an operand of some type, be it a number or variable. The trees are grouped by height.
|
|
|
| |
| ||||
Figure Example of Parse trees
6. Explain Parse Trees and Derivations
A derivation is a sequence of strings in V* which starts with a non-terminal in V-Σ and ends with a string in Σ*.
Let's consider the sample grammar
E → E+E | a
We write:
E ⇒ E+E ⇒ E+E+E ⇒a+E+E⇒a+a+E⇒a+a+a
but this is incomplete, because it doesn't tell us where the replacement rules are applied.
We actually need "marked" strings which indicate which non-terminal is replaced in all but the first and last step:
E ⇒ Ě+E ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a
In this case, the marking is only necessary in the second step; however it is crucial, because we want to distinguish between this derivation and the following one:
E ⇒ E+Ě ⇒ Ě+E+E ⇒a+Ě+E ⇒a+a+Ě ⇒a+a+a
We want to characterize two derivations as "coming from the same parse tree."
The first step is to define the relation among derivations as being "more left-oriented at one step". Assume we have two equal length derivations of length n > 2:
D: x1⇒ x2⇒ ... ⇒xn
D′: x1′ ⇒ x2′ ⇒ ... ⇒xn′
Where x1 = x1′ is a non-terminal and
xn = xn′ ∈ Σ*
Namely they start with the same non-terminal and end at the same terminal string and have at least two intermediate steps.
Let’s say D < D′ if the two derivations differ in only one step in which there are 2 non-terminals, A and B, such that D replaces the left one before the right one and D′ does the opposite. Formally:
D < D′ if there exists k, 1 < k < n such that
xi = xi′ for all i ≠ k (equal strings, same marked position)
xk-1 = uǍvBw, for u, v, w ∈ V*
xk-1′ = uAvB̌w, for u, v, w ∈ V*
xk =uyvB̌w, for production A → y
xk′ = uǍvzw, for production B → z
xk+1 = xk+1′ = uyvzw (marking not shown)
Two derivations are said to be similar if they belong to the reflexive, symmetric, transitive closure of <.
7. Explain Ambiguity in CFG
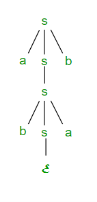
Suppose we have a context free grammar G with production rules: S->aSb|bSa|SS|ɛ
Left most derivation (LMD) and Derivation Tree:
Leftmost derivation of a string from staring symbol S is done by replacing leftmost non-terminal symbol by RHS of corresponding production rule.
For example: The leftmost derivation of string abab from grammar G above is done as:
S =>aSb =>abSab =>abab
The symbols in bold are replaced using production rules.
Derivation tree: It explains how string is derived using production rules from S and is shown in Figure.
Figure Derivation tree
Right most derivation (RMD):
It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.
For Example: The rightmost derivation of string abab from grammar G above is done as:
S => SS =>SaSb =>Sab =>aSbab =>abab
The symbols in bold are replaced using production rules.
The derivation tree for abab using rightmost derivation is shown in Figure.
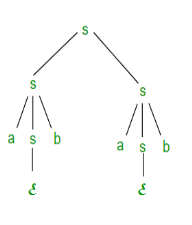
Figure Right most derivation
A derivation can be either LMD or RMD or both or none. For Example:
S =>aSb =>abSab =>abab is LMD as well as RMD
butS => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.
Ambiguous Context Free Grammar:
S => SS =>SaSb =>Sab =>aSbab =>abab
S =>aSb =>abSab =>abab
8. Explain Pumping lemma for context-free languages
Lemma: The language 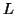 =
= 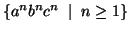 is not context free.
is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let 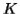 be the constant of the Pumping Lemma.
be the constant of the Pumping Lemma.
Considering the string 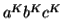 , where
, where 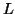 is length greater than
is length greater than 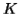 .
.
By the Pumping Lemma this is represented as 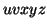 , such that all
, such that all 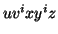 are also in
are also in 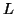 , which is not possible, as:
, which is not possible, as:
either 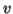 or
or 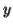 cannot contain many letters from
cannot contain many letters from 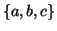 ; else they are in the wrong order .
; else they are in the wrong order .
if 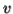 or
or  consists of a's, b's or c's, then
consists of a's, b's or c's, then 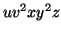 cannot maintain the balance amongst the three letters.
cannot maintain the balance amongst the three letters.
Lemma: The language  =
= 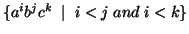 is not context free.
is not context free.
Proof (By contradiction)
Assuming that this language is context-free; hence it will have a context-free grammar.
Let  be the constant of the Pumping Lemma.
be the constant of the Pumping Lemma.
Considering the string  , which is
, which is 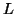 >
> 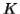 .
.
By the Pumping Lemma this must be represented as 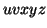 , such that all
, such that all 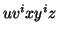 are also in
are also in 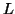 .
.
-As mentioned previously neither 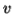 nor
nor 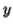 may contain a mixture of symbols.
may contain a mixture of symbols.
-Suppose 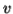 consists of a's.
consists of a's.
Then there is no way 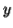 cannot have b's and c's. It generate enough letters to keep them more than that of the a's (it can do it for one or the other of them, not both).
cannot have b's and c's. It generate enough letters to keep them more than that of the a's (it can do it for one or the other of them, not both).
Similarly  cannot consist of just a's.
cannot consist of just a's.
-So suppose then that 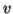 or
or 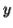 contains only b's or only c's.
contains only b's or only c's.
Consider the string 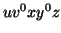 which must be in
which must be in 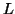 . Since we have dropped both
. Since we have dropped both 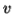 and
and 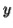 , we must have at least one b' or one c' less than we had in
, we must have at least one b' or one c' less than we had in  , which was
, which was 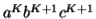 . Consequently, this string no longer has enough of either b's or c's to be a member of
. Consequently, this string no longer has enough of either b's or c's to be a member of 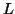 .
.
9. Brief Deterministic pushdown automata

10. Write Closure properties of CFLs
They are closed under −
Union
Let A1 and A2 be two context free languages. Then A1 ∪ A2 is also context free.
Example
Let A1 = { xnyn , n > 0}. Corresponding grammar G1 will have P: S1 → aAb|ab
Let A2 = { cmdm , m ≥ 0}. Corresponding grammar G2 will have P: S2 → cBb| ε
Union of A1 and A2, A = A1 ∪ A2 = { xnyn } ∪ { cmdm }
The corresponding grammar G will have the additional production S → S1 | S2
Concatenation
If A1 and A2 are context free languages, then A1A2 is also context free.
Example
Union of the languages A1 and A2, A = A1A2 = { anbncmdm }
The corresponding grammar G will have the additional production S → S1 S2
Kleene Star
If A is a context free language, then A* is also context free.
Example
Let A = { xnyn , n ≥ 0}. Corresponding grammar G will have P: S → aAb| ε
Kleene Star L1 = { xnyn }*
The corresponding grammar G1 will have additional productions S1 → SS1 | ε
Context-free languages are not closed under −