Unit - 3

Finite Fields and Confidentiality

Q1) What is Finite Fields?

A1) If you don't grasp what a finite field is, it's nearly impossible to properly comprehend any component of modern cryptography or several critical areas of general computer security.

 For example, you won't be able to understand AES (Advanced Encryption Standard) in Lecture 8 if you don't understand the concept of a finite field. AES is designed to be a modern successor for DES, as you recall from Lecture 3. The concept of a multiplicative inverse in a finite field underpins the substitution stage in AES.

For another example, if you don't comprehend finite fields, you won't be able to: You will be unable to comprehend the derivation of the RSA algorithm for public-key cryptography, which we shall discuss in the next sections.

12th Lesson

And if you don't know what public-key cryptography is, You won't be able to comprehend cryptography if you don't know what it's all about. A collection of current protocols (such as the SSH protocol you use)every day for secure access to other computers). communication over the internet You won't be able to comprehend why certificate-based user and document authentication has become so vital in computer security.

ˆ Digital rights management is another modern term that will perplex you if you are unfamiliar with public key cryptography. And, as I previously stated, you cannot comprehend public key cryptography without first understanding finite fields.

ˆ For another example, you will never comprehend the up-and-coming ECC algorithm (ECC stands for Elliptic Curve Encryption), which is currently in widespread usage and is often seen as a replacement for RSA in public key cryptography.

As you yourself can see, if you do not understand the concepts in this and the next three lectures, you might as well give up on learning computer and network security.

To put it very simply, a finite field is a finite set of numbers in which you can carry out the operations of addition, subtraction, multiplication, and division without error. In ordinary computing, division particularly is error prone and what you see is a high-precision approximation to the true result. Such high-precision approximations do not suffice for cryptography work. For cryptography, all arithmetic operations must be error-free. Here are some helpful hints for grasping the concept of a finite field:

1. set

2. group

3. abelian group

4. ring

5. commutative ring

6. integral domain

7. field

We'll start with the concepts of set and group in the next section.

Finite Groups vs. Infinite Groups (Permutation Groups) Infinite groups, or groups based on infinitely large sets, are a type of permutation group.

It's not difficult to imagine. Consider the following scenario:

– The set of all positive, negative, and zero integers

Addition, combined with the arithmetic process, makes up a

group.

– All even numbers (positive, negative, and zero) are included in this collection.

— is a group under the arithmetic addition operation.

The preceding two instances of groups demonstrate that a

A subset of a group can exist as its own entity. So that we can converse

regarding a group's subgroup

The set of all N N matrices over a given value of N

A group of real numbers is formed by the action of matrix addition.

- A group is defined as the set of all N N matrices over real numbers that are added together for a given value of N.

– The set of all three nonsingular matrices, as well as the set of all three nonsingular matrices plus the set of all three nonsingular matrices plus the set of all

8

Avi Kak's Computer and Network Security Lecture 4

As an operator, matrix multiplication creates a group.

RINGS We have a ring if we can define one more operation on an abelian group, provided the elements of the set satisfy specified conditions.

This new operation has its own set of attributes.

To distinguish it from the operation defined for the abelian,

We'll call the new operation multiplication in this group.

It's worth noting that the new method is referred to as "multiplication."

The term "operation" is just a notational convenience.

A ring is usually symbolised by the letters R, +, where R signifies the set.

'+' is the operator with respect to which R is an object.

R requires an additional operator, the abelian group.

make a ring.

Rings: Elements' Properties in Relation to the Ring Operator R must be closed in relation to the extra operator ".

R must be associative with the added variables.

‘' is an operator.

The extra operator (sometimes known as the "multiplication operator")

The group addition operator must be used to distribute. That is correct.

a × (b + c) = a × b + a × c

(a + b) × c = a × c + b × c

In such equations, the "multiplication" action is commonly depicted by simply concatenation:

a(b + c) = ab + ac

(a + b)c = ac + bc

Rings as examples

The set of all N N square matrices over the real numbers under the operations of matrix addition and matrix multiplication defines a ring for a given value of N.

A ring is the set of all even integers, positive, negative, and zero, under the operations of arithmetic addition and multiplication. A ring is the set of all integers under the operations of arithmetic addition and multiplication.

Q2) What do you mean by Fields?

A2) A field, indicated by the letters F, +, is an integral domain whose members meet the extra property:

ˆ Except for the element marked 0 (which is the identity element for the '+' operator), there must be a multiplicative inverse for every element an in F. That instance, if a F and a 6 equal 0, then there must be an element b F such that ab = ba = 1, where ‘1' symbolically signifies the element that serves as the multiplication operation's identity element. Such a b is frequently labelled as a 1 for a particular a. Remember that every element in a field has a multiplicative inverse, with the exception of the one that serves as the group operator's identity element.

Examples of Positive and Negative Fields

Q3) What do you mean by Modules Arithmetic?

A3) Many sophisticated encryption techniques are based on relatively simple modular arithmetic. The numbers we're working with in modular arithmetic are all integers, and the operations we're using are addition, subtraction, multiplication, and division. The only difference between modular arithmetic and the mathematics you learnt in elementary school is that all operations in modular arithmetic are done on a positive integer, i.e., the modulus.

Let's go over some fundamental topics before diving into modular arithmetic. According to the division theorem, there are always unique integers q and r such that a = qb + r and 0 r |b| exist for two integers a and b when b is 0.

Negative numbers must be handled with caution. As you can see from the examples above, they are frequently incongruent with their positive counterparts. Congruence is an equivalence relation that states that if a and b are congruent modulo n, they have no difference in modular arithmetic. As a result, we normally employ only n integers in modular n arithmetic: 0, 1, 2,..., n-1. All of the other numbers are congruent with at least one of the n numbers.

So, how do you use moduli to execute arithmetic operations? It's straightforward to compute addition, subtraction, and multiplication as in traditional arithmetic and reduce the result to the smallest positive value by dividing the modulus. Consider the following scenario:

12+9 ≡ 21 ≡ 1 mod 5

12-9 ≡ 3 mod 5

12+3 ≡ 15 ≡ 0 mod 5

15-23 ≡ -8 ≡ 2 mod 5

35*7 ≡ 245 ≡ 0 mod 5

-47*(5+1) ≡ -282 ≡ 3 mod 5

373 ≡ 50653 ≡ 3 mod 5 (exponentiation is just a shorthand for repeated multiplication)

Because we know that a1 b1 mod n and a2 b2 mod n hold for each integer a1, b1, a2, and b2, the following always holds for any integer a1, b1, a2, and b2:

a1+a2 ≡ b1+b2 mod n

a1-a2 ≡ b1-b2 mod n

a1*a2 ≡ b1*b2 mod n

For example, 35 ≡ 0 mod 5 therefore 35*7 ≡ 0*7 ≡ 0 mod 5. Also 37 ≡ 2 mod 5 so 373 ≡ 23 ≡ 8 ≡ 3 mod 5.

However, division is more difficult because division is not defined for all numbers. This implies that division in modular arithmetic is not always achievable. To begin with, division by zero is not defined in regular arithmetic, hence 0 cannot be the divisor. The tough part is that the modulus multiples are all congruent to 0. When the modulus is 6, for example, 6, -6, 12, -12, and so on are all congruent to 0. So not only is 4/0 not acceptable, but neither is 4/12 when the modulus is 6. Second, let's go back to the beginning: what does "division" in ordinary arithmetic mean? When we say 12 divided by 4 equals 3, we're referring to a number 3 that equals 3*4 = 12.

Q4) Describe Euclidean algorithms?

A4) The greatest number that divides two numbers is called the GCD. Factorizing both numbers and multiplying common prime factors is a straightforward approach to find GCD.

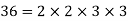
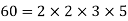
GCD = Multiplication of common factors

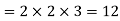
GCD Basic Euclidean Algorithm

The algorithm is based on the information below.

GCD remains same when a smaller number is subtracted from a larger one (a larger number is reduced). As a result, if we keep subtracting the larger of two, we get GCD.

Instead of subtracting, we can divide the smaller integer and the procedure will finish when we get to 0.

Q5) Describe Polynomial Arithmetic?

A5) We must first introduce the fascinating subject of polynomial arithmetic before moving on to our study of finite fields. We're dealing with polynomials in a single variable x, and there are three types of polynomial arithmetic to consider:

Ordinary polynomial arithmetic utilizing algebra's core rules

Polynomial arithmetic in which the coefficients' arithmetic is done modulo p; that is, the coefficients are in GF (p)

The coefficients in polynomial arithmetic are in GF(p), and the polynomials are defined modulo a polynomial m(x) whose largest power is some number n.

The first two classes are covered in this section, while the last class is covered in the next section.

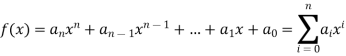
where the ai are elements of a known set of numbers called the coefficient set, and the 0 is a constant. Such polynomials are said to be defined over the coefficient set. A constant polynomial is a zeroth-degree polynomial that is merely a component of the set of coefficients. If a = 1, an nth-degree polynomial is said to be a monic polynomial.

We normally aren't interested in evaluating a polynomial for a specific value of x in abstract algebra [e.g., f(7)]. The variable x is frequently referred to as the indeterminate to underline this point.

The operations of addition, subtraction, and multiplication are all included in polynomial arithmetic.

As though the variable x were an element of S, these operations are defined in a natural fashion. Division is defined similarly, except it requires S to be a field. Real numbers, rational numbers, and Zp for p prime are examples of fields. It's worth noting that the set of all integers isn't a field and hence doesn't enable polynomial division.

By adding or deleting appropriate coefficients, addition and subtraction are performed. If this is the case,

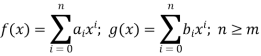
Then addition is defined as,

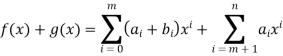
And multiplication is defined as:

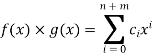
where

ck = a0bk1 + a1bk1 + ... + ak1b1 + akb0

For I > n, we treat ai as zero, and for I > m, we treat bi as zero. It's worth noting that the product's degree equals the total of the degrees of the two polynomials.

Q6) Define Placement of Encryption Function?

A6) We must decide what to encrypt and where the encryption function should be situated if encryption is to be used to counter attacks on confidentiality. This section begins by looking at the potential targets of security threats, then moves on to the two main ways of encryption placement: link and end to end.

Locations Where Confidentiality Attacks Could Happen

Consider a typical business organization's user workstation as an example. Figure depicts the many sorts of communications facilities that such a workstation might use, as well as the potential points of vulnerability.

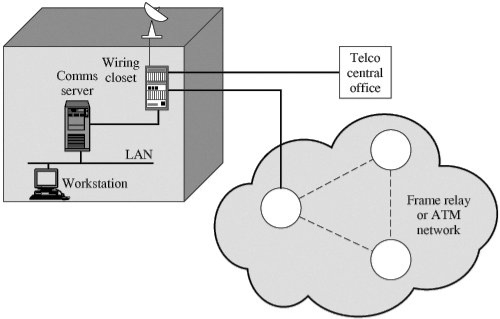
Figure: Points of Vulnerability

Workstations are typically connected to local area networks in most organizations (LANs). Typically, the user can connect to other workstations, hosts, and servers directly on the LAN or via bridges and routers to other LANs in the same building. This, then, is the first point of weakness. The key concern in this scenario is eavesdropping by another employee. A LAN is often a broadcast network, with transmissions from any station to any other station visible to all stations on the LAN medium. Frames are used to send data, with each frame including the source and destination addresses. An eavesdropper can monitor the traffic on the LAN and capture any traffic desired on the basis of source and destination addresses. If some or all of the LAN is wireless, then the opportunity for eavesdropping is increased.

Furthermore, the eavesdropper does not have to be a building employee. An intruder could get access to the LAN and monitor traffic if the LAN has a dial-in capability, which could be provided by a communications server or one of the LAN's hosts.

A router that links to the Internet, a bank of dial-out modems, or some other type of communications server nearly invariably provides access to the outside world from the LAN.

A line runs from the communications server to the wiring closet. The wire closet functions as a patch panel for connecting internal data and phone lines, as well as a staging area for exterior communications.

The wiring closet is vulnerable in and of itself. If an intruder gains access to the closet, he or she can probe each wire to see which ones are used for data transfer. The intruder can attach a low-power radio transmitter after isolating one or more wires. Signals generated as a result can be picked up from a nearby site (e.g., a parked van or a nearby building).

There are several ways to get out of the wiring closet. A basic arrangement offers access to the local telephone company's nearest central office. The wires in the closet are bundled together into a cable, which is then consolidated with other cables in the building's basement. A larger cable runs underground from there to the central office.

A link to a microwave antenna, either an earth station for a satellite link or a point-to-point terrestrial microwave link, may also be provided by the wire closet. The antenna link can be a local bypass to connect to a long-distance carrier or it can be part of a private network.

A link to a packet-switching network node may also be provided through the wire closet. This link could be a leased line, for example. a switched connection over a public telecommunications network or a direct private line Data travel across the network via a series of nodes and linkages between nodes until it reaches the node to which the destination end system is attached.

Q7) Define Traffic Confidentiality?

A7) Users may be concerned about security as a result of traffic analysis, as we described in Chapter 1. An opponent who knows the amount and length of messages sent and received between nodes may be able to figure out who is talking to whom. In a military conflict, this has clear ramifications. Even in commercial applications, traffic analysis may reveal data that the traffic generators would prefer to keep hidden. The following categories of information can be acquired from a traffic analysis attack, according to [MUFT89]:

Partners' identities

What is the frequency of communication between the partners?

Pattern of messages, length of messages, etc.

The occurrences that are linked to certain dialogues between two people.

or a large number of messages indicating the exchange of critical information

The occurrences that correspond to specific dialogues between certain partners.

Another issue with traffic is the creation of a covert channel using traffic patterns. A covert channel is a method of communication that is not intended by the communications facility's creators. Typically, the channel is used to send data in a way that is in violation of a security policy.

For example, an employee may seek to send information to an outsider in a way that is undetectable to management and involves only simple eavesdropping on the outsider's part. The two parties could devise a code in which a seemingly genuine message of less than a specific length corresponds to binary zero, while a larger message corresponds to binary one. Other schemes of this nature are possible.

Q8) Describe Key distribution?

A8) Traditionally, symmetric encryption had one major flaw: either the sender or the recipient had to produce a key and then deliver it to the other. A third party may steal or copy the key while it was in transit, allowing them to decipher any ciphertexts encrypted with that key.

Another issue is that communication parties require a high number of key pairs. The more people there are, the more difficult it becomes to manage. The formula is n(n-1)/2, where n denotes the number of communication parties.

If ten parties want to communicate securely with one another, they'll require 45 different key pairs: 10(10-1)/2 = 45.

If there were 100 communicating parties, this number would rise to 4,950!

This problem, known as the key distribution problem, afflicted anyone who wanted to use encryption until the 1970s, when GCHQ in the United Kingdom and Whitfield Diffie and Martin Hellman in the United States independently developed a method of distributing keys without actually sending the keys themselves. The approach is currently known as the Diffie–Hellman key exchange mechanism, after the British discovery was kept hidden for many years.

Symmetric encryption methods have the advantage of being highly quick at both encryption and decryption, making them excellent for sending huge amounts of protected data.

Q9) Describe Random number generation?

A9) We'll need to be able to produce random numbers sequences in order to apply the simulation-based techniques outlined in this book. The majority of the time, the programme we're using has a function that will take care of this for us. The runif() function in R, for example, can be used to create evenly distributed random integers over a defined interval.

Nonetheless, there are two points worth addressing in this context:

It's helpful to understand what goes on behind the scenes of these random number generators. How does a numerical sequence come to be?

R's built-in functions are only useful for distributions that are well-known or well-characterized. With many simulation-based techniques, though, we'll wish to create random numbers from distributions we've never seen before and for which no built-in function exists.

Q10) Describe Pseudo Random number?

A10) The truth is that R, like most other analytics software, does not produce true random numbers. R creates pseudo-random integers that look to be random but are actually deterministic. This method appears to be worse, but it is actually superior for two reasons. To begin with, creating true random numbers is time consuming and frequently requires the use of an external source of entropy/randomness. Second, true random numbers cannot be replicated.

As a result, if you wanted to recreate any simulation outcomes, you would never be able to do so.

We shall not go over the history of pseudo-random number generators (PRNGs). One thing to keep in mind is that this is a difficult field to enter and begin constructing your own PRNGs. It's helpful to understand how the systems function, but it's best to leave the details to the specialists.

The linear congruential generator is the most frequent type of PRNG used in scientific applications. The basic principle behind an LCG is that we start with a seed and then use a recurrence relation to generate pseudo-random integers. The form is found in the majority of LCGs.

Xn+1=(aXn+c) mod m