Unit - 5

Number theory and Public Key cryptography

Q1) Describe the Theory of Algorithmic numbers?

A1) Even if mathematics cannot be used to examine the security of cryptographic methods, it can be used to identify candidates for one-way and trapdoor one-way issues, such as integer factorization and discrete logarithm problems.

The Factorization of Integers

The factorization of integers is a simple candidate that comes to mind first:

While multiplying two prime integers p and q to get the product n = pq is simple,

Factoring n into its prime factors p and q is a difficult task.

Indeed, the multiplication of two integers of size k, p and q, yields

In k, it takes a quadratic amount of time. The factorization of any number of variables, however, is a complex process.

It's a little more complicated to write n as a product of prime numbers, such as n =. n = Q p vi

To begin, any integer n 2 has a factorization as a product of prime powers n = Q p vi,

where the pi are separate primes (which can only be divided by 1 and themselves) and vi are the valuations, which are represented by positive integers. Furthermore, up to a permutation of the factors, this factorization is unique.

Techniques that are generic

Many methods for factoring numbers have existed for a long time, ranging from trial-division through Pollard's approaches [57]. However, their complexity is really high: consider some of them for the integer n, where p is the lowest prime factor.

the trial-division requires p divisions to find the first prime factor, and up

to √ n divisions to fully factorize n – the Pollard’s ρ method [57], later improved by Brent [11], finds p after O(√p) iterations and fully factorizes n in O(n 0.106), on average– then some methods have been dedicated to special integers, such as the p−1-method which is quite fast when p−1 is smooth, and the p+ 1-method [80].

Anyway, all these methods that simply consist in trying to divide n by many primes provide algorithms which require an exponential amount of time w.r.t. k the size of n (k = ln n), typically exp(k/2) or exp(k/4) in the special case that n = pq, the product of two primes of similar size. Indeed, those numbers seem the strongest to factorize, then they will be used for cryptographic purpose.

Q2) Describe Fermat’s Theorems?

A2) Fermat’s Theorem Fermat’s theorem states the following: If p is prime and a is a positive integer not divisible by p, then

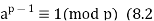
Proof: Consider the set of positive integers less than p: {1, 2, ......., p - 1} and multiply each element by a, modulo p, to get the set X = {a mod p, 2a mod p, ..... , (p - 1)a mod p}. None of the elements of X is equal to zero because p does not divide a. Furthermore, no two of the integers in X are equal. To see this, assume that ja == ka (mod p)), where 1 <= j < k <= p - 1. Because a is relatively prime5 to p, we can eliminate a from both sides of the equation [see Equation (4.3)] resulting in j === k (mod p). This last equality is impossible, because j and k are both positive integers less than p. Therefore, we know that the (p - 1) elements of X are all positive integers with no two elements equal. We can conclude the X consists of the set of integers {1, 2, ...., p - 1} in some order. Multiplying the numbers in both sets (p and X) and taking the result mod p yields.

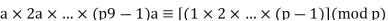
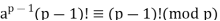
Because the ((p - 1)! term is substantially prime to p, we can cancel it is the result, and the proof is now complete.

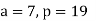
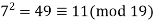
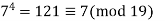
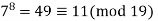
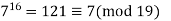
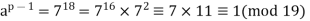
Fermat's theorem can also be expressed in a different way: If an is a positive integer and p is prime, then

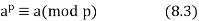
It's worth noting that the first form of the theorem [necessitates that a be relatively prime to p, but this form does not.

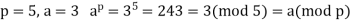
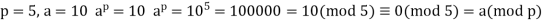
The Totient Function of Euler

Before presenting Euler's theorem, it's necessary to establish a key concept in number theory: Euler's totient function, denoted ϕ (n), which is defined as the number of positive integers less than n that are relatively prime to n. ϕ(1) = 1 is the standard convention.

DETERMINE ϕ(37) AND ϕ(35)

All positive numbers from 1 to 36 are re- latively prime to 37 since 37 is prime. As a result, ϕ(37) = 36.

To find ϕ(35), we make a list of all the positive numbers less than 35 that are related to it:

1, 2, 3, 4, 6, 8, 9, 11, 12, 13, 16, 17, 18 19, 22, 23, 24, 26, 27, 29, 31, 32, 33, 34, 

The list contains 24 numbers, thus ϕ(35) = 24.

The first 30 values of are listed in ϕ(n). The value ϕ(1) is devoid of meaning, however it is specified to be 1.

It should be obvious that when p is a prime number,

ϕ(p) = p - 1

Assume we have two prime numbers, p and q, where p!= q. Then, for n = pq, we can establish that

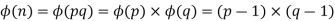
To see that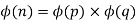

Consider that the set of positive integers less that n is the set [1, …, (pq-1)]. The integers in this set that are not relatively prime to n are the set { p, 2p, … (q-1)p } and the set {q, 2q, …,(p-1)q}. Accordingly,

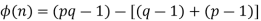
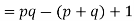
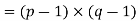
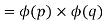
n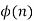
1	1
2	1
3	2
4	2
5	4
6	2
7	6
8	4
9	6
10	4

n
11	10
12	4
13	12
14	6
15	8
16	8
17	16
18	6
19	18
20	8

n
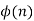21	12
22	10
23	22
24	8
25	20
26	12
27	18
28	12
29	28
30	8

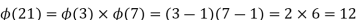
Where the 12 integers are {1,2,4,5,8,10,11,13,16,17,19,20}

Q3) Describe Euler’s Theorems?

A3) Euler’s theorem states that for every a and n that are relatively prime: Proof: Equation is true if n is prime, because in that case, ϕ(n) = (n - 1) and Fermat’s theorem holds. However, it also holds for any integer n.

 Recall that f(n) is the number of positive integers less than n that are relatively prime to n. Consider the set of such integers, labeled as R = {x1, x2, ...... , xϕ(n)} That is, each element xi is a unique positive integer less than n with gcd(xi, n) = 1. Now multiply each element by a, modulo n: S = {(ax1 mod n), (ax2 mod n), ....., (axϕ(n) mod n)} The set S is a permutation6 of R, by the following line of reasoning: 1. Because a is relatively prime to n and xi is relatively prime to n, axi must also be relatively prime to n. Thus, all the members of S are integers that are less than n and that are relatively prime to n. 1. There are no duplicates in S. Refer to Equation (4.5). If axi mod n = axj mod n, then xi = xj. Therefore,

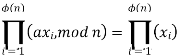
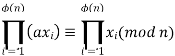
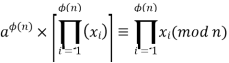
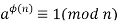
which brings the proof to a close. This is the same argument that was used to prove Fermat's theorem.

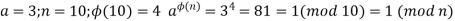
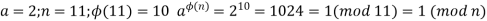
An alternative form of the theorem is also useful, as it is for Fermat's theorem:

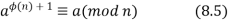
The first form of Euler's theorem [Equation] needs that a be relatively prime to n, just like Fermat's theorem, but this form does not.

Q4) What do you mean by Testing for primality?

A4) Many cryptographic algorithms require the random selection of one or more very big prime numbers. As a result, we must determine whether or not a particular huge integer is prime. There is no simple yet effective way to complete this assignment.

In this section, we'll look at a popular and appealing algorithm. You might be surprised to hear that this algorithm produces a number that isn't always a prime. The method, on the other hand, can produce a number that is virtually surely a prime. This will be clarified shortly. A deterministic approach for obtaining primes is also mentioned. The section comes to a close with a consideration of prime distribution.

Q5) What do you mean by Algorithm of Miller-Rabin?

A5) Also known as the Rabin-Miller algorithm, Rabin-Miller test, or Miller-Rabin test in the literature.

Miller and Rabin's approach [MILL75, RABI80] is commonly used to test a large number for primality. We need some context before we can explain the algorithm. To begin, any positive odd integer n 3 can be written as:

n 1 = 2kq, where k is greater than zero and q is odd

Note that (n 1) is an even number to see this. Then divide (n 1) by 2 until you have an odd integer q, which will take a total of k divisions. If n is a binary number, the result is obtained by shifting the number to the right until the rightmost digit is a 1, resulting in a total of k shifts.

Q6) What are the Characteristics of Prime Numbers?

A6) The first characteristic is as follows:

 If p is prime and an is a positive integer less than p, a2 mod p = 1 if and only if a mod p = 1 or a mod p = 1 mode p = p 1. (a mode p) (a mode p) = a2 mod p, according to modular arithmetic standards. As a result, if either a mode p or a mod p = 1, a2 mod p = 1. In contrast, if a2 mod p = 1, then (a mod p)2 = 1, which is only true if mod p = 1 or mod p = 1.

The second characteristic is as follows:

Let p be a prime number that is greater than or equal to 2. With k > 0 q odd, we can write p 1 = 2kq. Let a be any number between 1 and 1 a p 1. Then one of the following two conditions applies:

1 modulo p is congruent to aq. That is, aq mod p = 1, or aq 1 (mod p) = 1.

1 modulo p is congruent to one of the numbers aq, a2q, a4q,..., a2k-1q. That is, there is a number j in the range (1 a2j-1q mod p = 1 mod p = p 1, or equivalently, a2j-1q 1 (mod p Proof: According to Fermat's theorem [Equation an1 1 (mod n) is prime. p 1 = 2kq is the answer. As a result, we can deduce that ap1 mod p = a2kq mod p = 1. As a result, if we examine the numerical series, we can see that

Equation

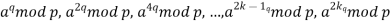
The value of the last number in the list is 1. In addition, each number in the list is the square of the one before it. As a result, one of the following scenarios must be true:

The first number on the list equals 1, as do all subsequent numbers on the list.

Some of the numbers on the list do not add up to 1, but their square mod p does. We know that the only number that meets this criterion p 1 is due to the first property of prime numbers, as mentioned above. As a result, the list has an element equal to p 1 in this situation.

The proof is now complete.

Algorithm Specifications

As a result of these considerations, we may conclude that if n is prime, The first member in the list of residues, or remainders, (aq, a2q,..., a2k-1q, a2kq) modulo n equals 1; otherwise, n is composite (i.e., not a prime). On the other hand, just because the criterion is met does not mean that n is prime. If n = 2047 = 23 x 89, for example, n 1 = 2 x 1023. 21023 mod 2047 = 1, indicating that 2047 satisfies the criterion but is not prime.

Q7) Describe the Chinese remainder theorem?

A7) We are given two arrays num[0..k-1] and rem[0..k-1]. In num[0..k-1], every pair is coprime (gcd for every pair is 1). We need to find minimum positive number x such that:

 x % num[0] = rem[0],

 x % num[1] = rem[1],

.......................

 x % num[k-1] = rem[k-1]

Basically, we are given k numbers which are pairwise coprime, and given remainders of these numbers when an unknown number x is divided by them. We need to find the minimum possible value of x that produces given remainders.

 Examples:

 Input: num[] = {5, 7}, rem[] = {1, 3}

Output: 31

Explanation:

31 is the smallest number such that:

 Input: num[] = {3, 4, 5}, rem[] = {2, 3, 1}

Output: 11

 Explanation:

11 is the smallest number such that:

Chinese Remainder Theorem states that there always exists an x that satisfies given congruences. Below is theorem statement adapted from wikipedia. Let num[0], num[1], …num[k-1] be positive integers that are pairwise coprime. Then, for any given sequence of integers rem[0], rem[1], … rem[k-1], there exists an integer x solving the following system of simultaneous congruences.

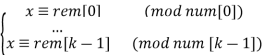
Furthermore, all solutions x of this system are congruent modulo the product,

prod=num[0]*num[1]*…*num[k-1]. Hence

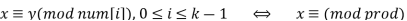
The existence of an x is obvious in the first part. When the by-product of n[0], num[1],... num[k-1] is divided by-product of n[0], num[1],... num[k-1], all solutions (including the minimum one) generate the same remainder. The product in the case above is 3*4*5 = 60. And 11 is one among the options; others include 71, 131, and so on. When divided by 60, all of these answers generate the same remainder, i.e., they are of the type 11 + m*60 where m >= 0.

To find x, a naive approach is to start with 1 and increase it one by one, checking to see if dividing it by given items in num[] gives comparable remainders in rem[]. We return the x once we've found one.

Q8) Define Discrete Logarithms in Cryptography?

A8) We discussed how to build numerous public-key cryptosystems that depended on the computational difficulty of factoring huge integers, and we introduced public-key cryptography. In this chapter, we'll look at another computationally challenging number theory problem: computing discrete logarithms.

The idea is to use that problem as the foundation for cryptographic systems in the future. We'll talk about it in detail.

The ElGamal public-key cryptosystem and the Die-Hellman key exchange technique are described, followed by some approaches for key exchange.

Discrete logarithms are computed.

Definition: If b is a modulo m unit and a is another unit with a ≡ b d (mod m), we say d is the d is the discrete logarithm of a modulo m to the base b, and write d = logb(a)

Note that we implicitly consider the discrete logarithm to be defined only modulo b's order. Some The discrete logarithm, on the other hand, is defined as the lowest positive integer such that a ≡ b d(mod m) if one exists; nonetheless, this definition is somewhat ambiguous (as is the case with the definition of modular congruence).

Too constricting

The discrete logarithm gets its name from the fact that its denition is similar to that of the discrete logarithm.

logb is a common logarithm.

(a)              = d (mod k) is the same a ≡ b d where k is the order of b modulo m. (Compare to the denition of the real-valued logarithm: logb (y) = x is equivalent to y = b x .) ◦ Example: Modulo 14, we have log3 11 = 4 since 3 4 ≡ 11 (mod 14). It is better to write log3 11 ≡ 4 (mod 6), since the order of 3 modulo 14 is 6.

Q9) Define Public Key Cryptanalysis?

A9) Public Key Cryptography is a cryptographic technology that encrypts and decrypts data using "two different keys." As a result, it's often referred to as asymmetric-key cryptography. Public key cryptography differs from traditional symmetric key cryptography in that it is entirely based on a "invertible mathematical" function.

It's not that symmetric key cryptography is inefficient compared to public key cryptography, or that public key cryptography is superior. The length of the key and the calculation required to crack the encrypted cypher text determine the security of any cryptosystem. In this section, we'll go over public key cryptography in general, as well as its requirements.

To avoid a brute force attack, the key size should be kept large enough that calculating encryption and decryption is hard for an adversary. However, the key size should not be so huge that computing practical encryption and decryption becomes impossible.

Another sort of public key cryptography attack is when an adversary tries to compute the private key using the public key.

A possible message assault is another form of attack. If an adversary knows that a 56-bit key is used to encrypt a message from a specific sender. Then, because the sender's public key is available to everyone, he would simply encrypt all feasible 56-bit keys using the sender's public key.

Q10) Describe Public Key Cryptosystem Principles?

A10) Any cryptosystem must adhere to two key principles: confidentiality and authenticity. The symmetric cryptosystem has a difficulty with these two concepts, as we've seen.

The problem with confidentiality in symmetric cryptography is that we all know that a secret key is needed to encrypt and decrypt the message in symmetric encryption. As a result, this key must be shared by both communication parties by any means possible, or they must rely on a third party, such as a key distribution centre, to distribute the key. However, relying on a third party puts the secret key's confidentiality at risk once more.

Authentication was also a problem with Symmetric Key. To become widely used, digital signatures were required, which assure all parties that a certain communication was sent by a specific individual.

Both of these principles, namely confidentiality and authenticity, are successfully achieved by the public key cryptosystem. Let's talk about it.

The first step is to encrypt the message with the sender's private key. Now that the message has been encrypted with the sender's private key, it can be verified that the message was written by the sender. This fulfils the role of the digital signature.

Q11) Describe Cryptosystem with Public Keys?

A) The following are the six elements of any public key cryptography algorithm:

Text in Plain Language

This is a legible message that the algorithm receives as input. The plain text is encrypted in blocks using a public key technique.

Algorithm for Encryption

The encryption algorithm is applied to plain text, which undergoes a number of modifications.

Keys that are both public and private

These are a group of keys, one of which is used for encryption and the other for decryption. The encryption algorithm's modification of plain text is determined by the key picked from the set to encrypt the plain text.

Cipher Text

The output of the encryption algorithm is Cipher Text. The resulting cypher text is entirely dependent on the key chosen from the public and private key sets. Both of these keys would yield separate cypher texts if used with plain text one at a time.

Algorithm for Decryption

This would accept the cypher text as the output of the encryption technique and apply the relevant key to generate the original plain text.

Q12) What do you mean by RSA algorithm?

A12) The RSA algorithm utilizes asymmetric cryptography, which means it employs both a public and a private key (i.e. two different, mathematically linked keys). A public key is shared openly, but a private key is kept private and must not be shared with anybody.

The RSA algorithm is named after Ron Rivest, Adi Shamir, and Leonard Adleman, who devised it in 1978.

How does it work?

In the example above, the RSA technique ensures that the keys are as secure as possible. The steps below demonstrate how it works:

The first step is to generate the keys.

xx and yy are two huge prime numbers. The prime numbers should be large enough that figuring them out will be tough.

Calculate n = x * yn=x∗y.

The totient function is calculated as phi(n) = (x-1) (y-1) ϕ(n)=(x−1) (y−1).

Choose an integer ee such that it is co-prime to phi(n)(n) and 1 < e < \phi(n)1<e<ϕ(n). The public key is made up of the numbers (n,e)(n,e).

Note: If the sole positive integer that divides two integers is 1, they are co-prime. The extended Euclidean technique can be used to find dd such that e.d = 1e.d=1 modmod \phi(n)ϕ(n).. The private key is made up of the pairs (n,d)(n,d).

2. The use of encryption

The ciphertext CC is calculated from a plaintext PP, which is represented as a number:

C=P​e​​ mod n.

3. Unlocking the code

The plaintext can be found using the private key (n, d) (n, d):

P=C​d​​ mod n.