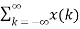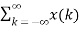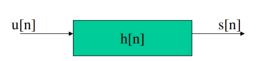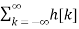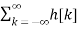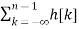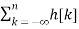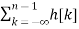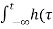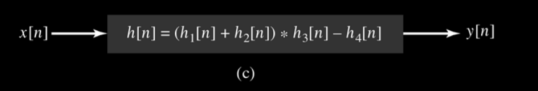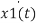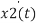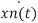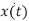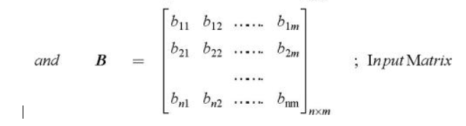x(n) = Then the output y(n) = T [
Figure . Step response The step response of a discrete-time LTI system is the convolution of the unit step with the impulse response- s[n]=u[n]*h[n]. -------------------(1) commutative property of convolution, s[n]=h[n]*u[n]. ----------------------------------------(2) That means s[n] is the response to the input h[n] of a discrete-time LTI system with unit impulse response u[n].
Figure . LTI discrete time
s[n] = Since u [n- k]< 0 is for n- k< 0, i.e. k> n and 1 for n -k> 0, i.e. k≤ n. Therefore, That is the step response of the discrete LTI system is the running sum of its impulse response. s[n-1] = s[n] – s[n-1] = h[n] = s[n] – s[n-1] From here h[n] can be recovered from s[n] , the impulse response of discrete-time LTI system is the first difference of its step response. For continuous time system The unit step response is the running integral of its impulse response. s(t) = The unit impulse response is the first derivative of the unit step response: - h(t) = ds(t)/dt = s’(t)
|
Figure . I/O relation
|
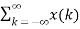 ∂(n-k) Then the output y(n) = T [
∂(n-k) Then the output y(n) = T [ 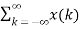 ∂(n-k)]Using linear property of the system, interchange the system operator T with the summation x(k) to obtain y(n) =
∂(n-k)]Using linear property of the system, interchange the system operator T with the summation x(k) to obtain y(n) = 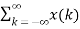 T [ ∂(n-k)]Now y(n) =
T [ ∂(n-k)]Now y(n) = 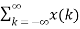 h(n,k)For a time-invariant system h(n,k) = h(n-k)Therefore y(n) =
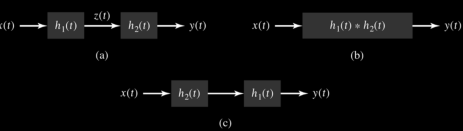
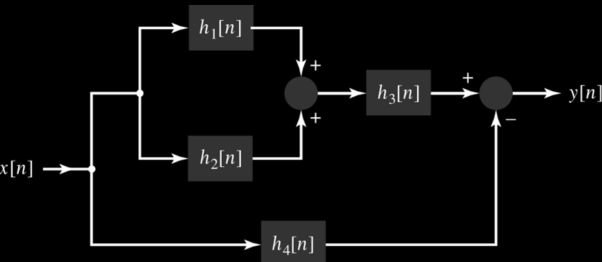
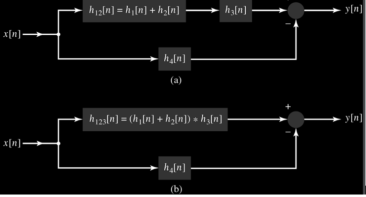
h(n,k)For a time-invariant system h(n,k) = h(n-k)Therefore y(n) = 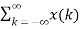 h(n-k)Thus, the output of the LTI system is given by the weighted sum of the time-shifted responses. This sum is termed as convolution sum represented as y(n) = x(n) * h(n) where * denotes convolution. Q3) Explain cascade connections?A3) Consider the cascade connection of two LTI systems, as illustrated in Fig. (a). Let z(t) be the output of the first system and therefore the input to the second system in the cascade. The output is expressed in terms of z(t) as 𝑦 (𝑡) = 𝑧(𝑡) ∗ ℎ2(𝑡)Substituting for z(t), we gety(t) =
h(n-k)Thus, the output of the LTI system is given by the weighted sum of the time-shifted responses. This sum is termed as convolution sum represented as y(n) = x(n) * h(n) where * denotes convolution. Q3) Explain cascade connections?A3) Consider the cascade connection of two LTI systems, as illustrated in Fig. (a). Let z(t) be the output of the first system and therefore the input to the second system in the cascade. The output is expressed in terms of z(t) as 𝑦 (𝑡) = 𝑧(𝑡) ∗ ℎ2(𝑡)Substituting for z(t), we gety(t) = 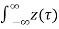 h2(t-τ) dτPutting for z(t) we get y(t) =
h2(t-τ) dτPutting for z(t) we get y(t) = 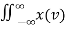 h1(τ-v) h2(t-τ) dv dτ =
h1(τ-v) h2(t-τ) dv dτ = 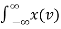 h(t-τ) dv= h(t) * h(t)
h(t-τ) dv= h(t) * h(t)
|
|
|
|
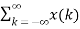 h(n-k) = =
h(n-k) = = 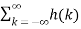 x(n-k)----------------------(1)The magnitude of the output is given by |y(n)| = |
x(n-k)----------------------(1)The magnitude of the output is given by |y(n)| = | 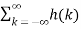 x(n-k)|-------------------------(2)We know that the magnitude of the sum of terms is less than or equal to the sum of the magnitudes, hence |y(n)| = |
x(n-k)|-------------------------(2)We know that the magnitude of the sum of terms is less than or equal to the sum of the magnitudes, hence |y(n)| = | 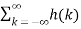 x(n-k)|≤
x(n-k)|≤ 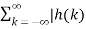 || x(n-k)| --------------------(3)Let the bounded value of the input be equal to M then eq(3) can be written as |y(n) | ≤ M
|| x(n-k)| --------------------(3)Let the bounded value of the input be equal to M then eq(3) can be written as |y(n) | ≤ M 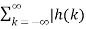 |------------------------------(4)The above condition is satisfied when
|------------------------------(4)The above condition is satisfied when 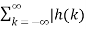 | < ∞ ------------------------(5)Therefore, the necessary and sufficient condition for stability is
| < ∞ ------------------------(5)Therefore, the necessary and sufficient condition for stability is 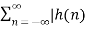 | < ∞ -----------------------(6)Therefore, the LTI system is stable if its impulse response is absolutely summable. Q5) Explain causality of LTI system?A5) If x(t) = ∂(t) then according to convolution theorem y(t) = x(t) * h(t) = h(t) * ∂(t) = h(t)A casual system is one where the output at the present instant does not anticipate input from future instants. X(t) , t<to ------- y(t) , t<to An LTI system is casual if and only if h(t) = L (δ(t)) = 0 , t<0 The impulse response of the system has to be zero for negative time for the system to be casual. For discrete time system the impulse response of the sequence h[n] of LTI system has to be right -sided sequence h[n] = L (δ[n]) = 0 , n<0 Q6) Explain the system representation for differential equation?A6) An LTI system is specified by equation d 2 y(t)/ dt 2 + 5 d y(t) /dt + 6 y(t) = dx(t) / dt + 4 x(t) The input is x(t) = e -t u(t) Find the natural response for initial conditions:y (0+) = 3 d y(0+)/dt =0Forced response Total response.Given d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t) = d x(t)/dt + 4 x(t)The natural response can be obtained by equating input terms in differential equation to zero. d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t)=0The characteristic equation is
| < ∞ -----------------------(6)Therefore, the LTI system is stable if its impulse response is absolutely summable. Q5) Explain causality of LTI system?A5) If x(t) = ∂(t) then according to convolution theorem y(t) = x(t) * h(t) = h(t) * ∂(t) = h(t)A casual system is one where the output at the present instant does not anticipate input from future instants. X(t) , t<to ------- y(t) , t<to An LTI system is casual if and only if h(t) = L (δ(t)) = 0 , t<0 The impulse response of the system has to be zero for negative time for the system to be casual. For discrete time system the impulse response of the sequence h[n] of LTI system has to be right -sided sequence h[n] = L (δ[n]) = 0 , n<0 Q6) Explain the system representation for differential equation?A6) An LTI system is specified by equation d 2 y(t)/ dt 2 + 5 d y(t) /dt + 6 y(t) = dx(t) / dt + 4 x(t) The input is x(t) = e -t u(t) Find the natural response for initial conditions:y (0+) = 3 d y(0+)/dt =0Forced response Total response.Given d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t) = d x(t)/dt + 4 x(t)The natural response can be obtained by equating input terms in differential equation to zero. d 2 y(t) / dt 2 + 5 d y(t)/dt + 6 y(t)=0The characteristic equation is 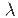 + 6=0
+ 6=0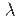 2 = -3
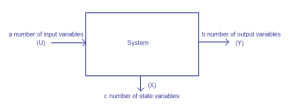
2 = -3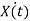 = AX(t) + B U(t) ------ state equations Y(t) = CX(t) + DU(t) --------- output equations X
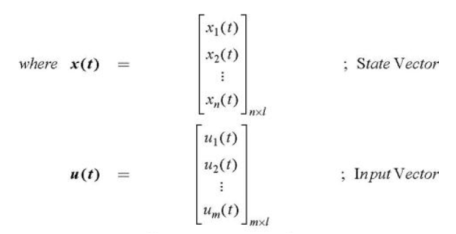
= AX(t) + B U(t) ------ state equations Y(t) = CX(t) + DU(t) --------- output equations X 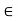 R n : state vector U
R n : state vector U 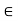 R m : input vector Y
R m : input vector Y 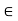 R p : output vector A nxn : System Matrix B nxm : Input matrix C pxn : Output matrix D pxm : Coupling matrix Number of states usually equals to degree of the system. Set of states in not unique for the system.
R p : output vector A nxn : System Matrix B nxm : Input matrix C pxn : Output matrix D pxm : Coupling matrix Number of states usually equals to degree of the system. Set of states in not unique for the system.
|
…….
Similarly the output variables can be written as a linear combination of system states and inputs that is y1(t) = c11 x1(t) + c12 x2(t) +……..+ c1n xn(t) +d11 u1(t) + d12 u2(t) + …+ d1mum(t) ---------------------------------------(1) y2(t) = c21 x1(t) + c22 x2(t) +……..+ c2n xn(t) +d21 u1(t) + d22 u2(t) + …+ d2mum(t)--------------------------------------------(2) ------ yp(t)= cp1x1(t) + cp2x2(t) + ………..+ cpnxn(t) + dp1u1(t) + dp2u2(t) +….+dpmum(t) where coeffecients cij = i=1,2,p; j=1,2,p: k=1,2,m are constants. In vector form y(t)= Cx(t) + D u(t) ---------Output Equation. |
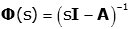 where I is the identity matrix. The time domain state transition matrix, φ(t), is simply the inverse Laplace Transform of Φ(s). Q10) Explain the notion of frequency response and its relation to impulse response?A10) The output given by the convolution sum is y(n) =
where I is the identity matrix. The time domain state transition matrix, φ(t), is simply the inverse Laplace Transform of Φ(s). Q10) Explain the notion of frequency response and its relation to impulse response?A10) The output given by the convolution sum is y(n) = 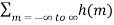 x (n-m) --------------------------(1)Suppose that the input is a complex exponential function, where for all n ∈ Integers, then x(n) = e jwn ----------------------------------(2)Then y(n)=
x (n-m) --------------------------(1)Suppose that the input is a complex exponential function, where for all n ∈ Integers, then x(n) = e jwn ----------------------------------(2)Then y(n)= 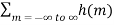 ejw(n-m) -----------(3) = e jwn
ejw(n-m) -----------(3) = e jwn 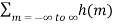 e-jwm -------(4)When the input is the complex exponential with frequency ω , then the output is given by y(n) = H(w) e jwn -----------------------(5)where H(ω ) is called the frequency response. Comparing these two expressions for the output we see that the frequency response is related to the impulse response by H(w) =
e-jwm -------(4)When the input is the complex exponential with frequency ω , then the output is given by y(n) = H(w) e jwn -----------------------(5)where H(ω ) is called the frequency response. Comparing these two expressions for the output we see that the frequency response is related to the impulse response by H(w) = 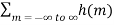 eimw -----------(6)H(ω ) is called the discrete-time Fourier transform (DTFT) of h(n).
eimw -----------(6)H(ω ) is called the discrete-time Fourier transform (DTFT) of h(n).