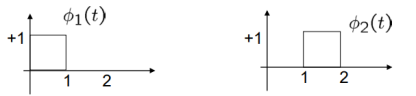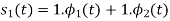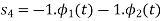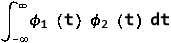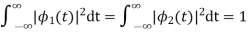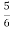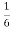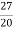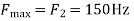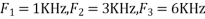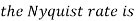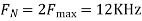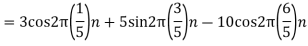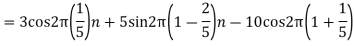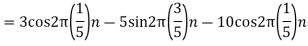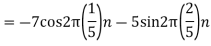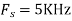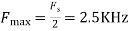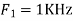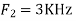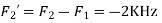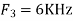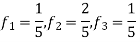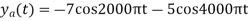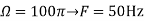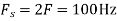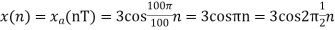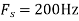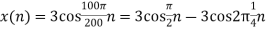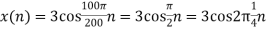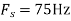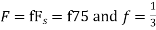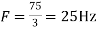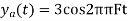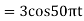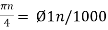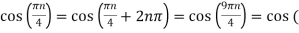|
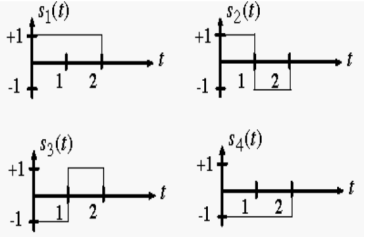
By inspection, the signals can be expressed in terms of the following two basis functions:
Note that the basis is orthogonal
Also note that each these functions have unit energy
We say that they form an orthonormal basis.
|
 y[n-1]+
y[n-1]+ y[n-2]=1+3-n. Given y[-2] = 0 and y[-1]=2
y[n-2]=1+3-n. Given y[-2] = 0 and y[-1]=2A2) For homogeneous solution Y[n] = rn rn- rn-2(r2- Solving above equation we get r= Roots are distinct so the solution will be of the form y[n] = p1 y[n] = p12-n + Particular Solution:
The complete solution of any difference equation is the sum of homogeneous solution and the particular solution. |
 y[n-1]-
y[n-1]-  y[n-2]?
y[n-2]?A3) As x[n] = 3n From table the particular solution will be y[n] = k3n y[n] = x[n]+ k3nu(n) = 3nu(n)+ Finding k for n≥2 K 32 = 32+ 9k- k= 27/20 y[n]= |
A4)
We know, X[n] =x(nT) = cos(200πnT) = cos(2πn/3) , where n= -1,0,1,2……
The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3. |

A6) The frequency in the analog signal
The largest frequency is
The Nyquist rate is
|

 . What is discrete time signal obtained after sampling?
. What is discrete time signal obtained after sampling?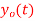 we can reconstruct from the sample if we use ideal interpolation?
we can reconstruct from the sample if we use ideal interpolation?A7)
For Hence
So that normalizing frequencies are
The analog signal that we can recover is
|

 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling?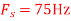 , what is the discrete time signal after sampling?
, what is the discrete time signal after sampling?A8) a. The minimum sampling rate is
And the discrete time signal is
b. if
c. If Fs=75Hz , the discrete time signal is
d. For the sampling rate
So, the analog sinusoidal signal is
|
A9) Taking T= 1/1000s cos(πn/4) =x[n] = x(nT) = cos (Ø0n/1000) Ø1 is easily computed as Ø1 = 250π
Ø2 can be obtained by noting the periodicity of a sinusoid:
Ø2 = 2250π |
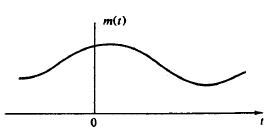
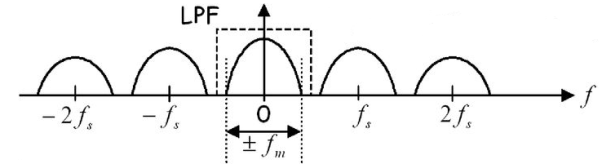
A10) In sampling the signal m(t) is multiplied with periodic pulse train. Let M(ω) the spectrum of the input signal be band limited with the maximum frequency of fm as shown in figure 1.
Figure: 1 Spectrum of input Signal
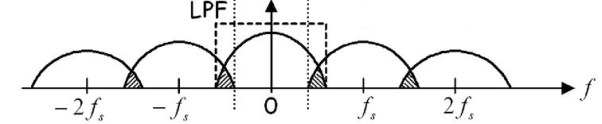
Figure: 2 (fs>2 fm) Figure: 3 (fs<2 fm) The frequency spectrum of this signal when impulse sampled is plotted in figure 2 (for fs>2 fm). In figure 3 for (fs<2 fm). From figure 2 and figure 3 we can conclude that as long as fs≥2fm the original signal is preserved in the sampled signal and can be extracted from it by the low pass filter. This is known as Shannon’s Sampling theorem. This theorem states that the information contained in a signal is fully preserved in the sampled form as long as the sampling frequency is at least twice the maximum frequency contained in the signal. |