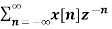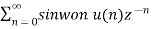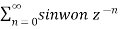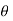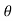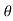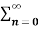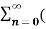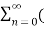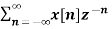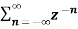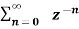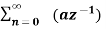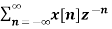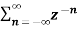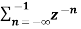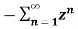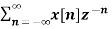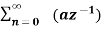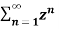A1) X(z) =
X(z) =
=
= 1/2j
= 1/2j
1/2j[ 1/1-ejw0z-1 – 1/1-e-jw0z-1]
= sin w0 z-1/ 1-2cos(wo)z-1 + z-2 ROC |z| >1
|
A2) We know that x(n) = an u(n) is
X(z) = 1/1/az-1
By using time shifting property we have Z{ x(n-k)} = z-k X(z)
Therefore
Z{an-1 u(n-1)} = z-1/ 1-az-1 = 1/z-a. ROC |z| > |a| |
A3) Z{ cos w0n} = 1- (cos w0) z-1/ 1 –(2 cos w0) z-1 + z-2
Since w0=π/2
Z{ cos π/2 n u(n)} = 1/1 + z-2
Using exponential sequence property
Z{ an x(n) } = X(a-1 z)
Z{ an cos nπ/2} = 1/1+(a-1z)-2 = 1/ 1 + a2/z2 = z2/ a2 + z2
|
A4) The z-transform of unit step sequence is given by
Z{u(n)} = z/z-1
Z{ n u(n)} = -z d/dz (z/z-1)
= z/(z-1)2 |
A5) X1(z) = 1/ 1- (1/3)z-1 X2(z) = 1/1- (1/5) z-1
X(z) = 1/1-(1/3)z-1 . 1/1-(1/5) z-1
Using z-transform find the convolution of two sequences.
x1(n) = {1,2,-1,0,3} x2(n) = { 1,2,-1}
Z{ x1(n) * x2(n)} = X1(z) . X2(z)
X1(z) = 1 + 2z-1 – z-2 + 3 z-4
X2(z) = 1 + 2z-1 – z-2
(1 + 2z-1 – z-2 + 3 z-4 ) (1 + 2z-1 – z-2 )
= 1 + 4z-1 + 2z-2 – 4 z- 3 + 4 z-4 + 6 z- 5 – 3 z-6
|
A6) Z{(sin w0n ) u(n)} = sin w0 z-1/ 1 -2 (cos w0) z-1 + z-2
Z{an x(n)} = X(a-1 z)
Therefore
Z{ rn sin(w0n) u(n) } = (sin w0) (r-1 z)-1/ 1- 2 (cos w0)(r-1z)-1 + (r-1z)-2
= r(sinw0) z-1/ 1-2r(cos w0) z-1 + r2 z-2
|
A7) X(z)= log(1-az-1)
Differentiating both side we get
d/dz X(z) = 1/1-az-1 (a z-2) = az-2/1- az-1
-z d/dz { X(z)} = -az-1/1-az-1
= -az-1[ 1/1-az-1]
= -a Z[ a n-1 u(n-1)] -------- (1)
From differentiation property
Z{ n x(n)} = -z d/dz [ X(z)] ------- (2)
Comparing (1) and (2) we get
n x(n) = -a [ a n-1 u(n-1)]
or x(n) = -a [a n-1 u(n-1)]/n |
A8) x(n) =1/2 (n2 + n) (1/3) n-1 u(n-1)
=½ n2 (1/3) n-1 u(n-1) +1/2 n (1/3) n-1 u(n-1)
We know that
Z[(1/3) n u(n)] = z/ z-1/3
Using time-shifting property
Z{(1/3) n-1 u(n-1)] = 1/ z- 1/3
Z [ n (1/3) n-1 u(n-1)] = -z d/dz [1/z-(1/3)]
=-z d/dz( 1/z-1/3)= -z [-1/(z-1/3) 2]= z/ (z-1/3)2
Z [ n2 (1/3) u(n-1)] = -z d/dz [ z/(z-1/3)2]
= z(z+1/3)/(z-1/3)2
= -z [ (z-1/3)2 -2z(z-1/3)/(z-1/3)4
= z(z+1/3)/(z-1/3)3
X(z) = ½[z(z+1/3)/(z-1/3)3 + z/ (z-1/3)2]
= z2/(z-1/3)3 |
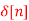 + 3
+ 3 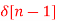 + 5
+ 5 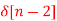 + 2
+ 2 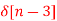
A9)
X(z) = 2 + 3 z-1 + 5 z -2 + 2 z -3
|
A10) X(z) =
= 1 for n≥0
=
=
This is a geometric series of infinite length that is
a + ar + ar2 + ………….. ∞ = a /1-r if |r| <1
Then from equation (3) it converges when |az-1| < 1 or |z| >|a|
Therefore
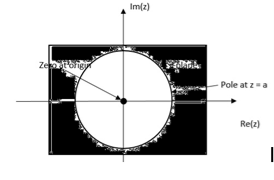
X(z) = 1/ 1-az-1: ROC |z| > |a|
Fig 2 ROC |z|>|a|
|
A11)X(z) =
X(z) = = 1 for n ≤ -1 =
= b-1z/1- b-1z = z/ z-b = 1/ 1-bz-1 |z| < |b|
Fig 3 ROC |z|<|b|
|
A12) X(z) =
=
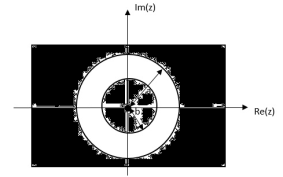
= z/z-a + z/z-b ROC |a| < |z| < |b|
Fig 4 ROC |a| < |z| < |b|
|b|< |a|
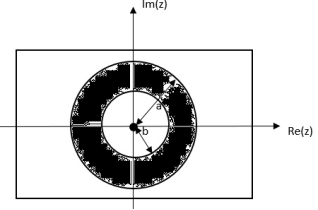
Fig 5 ROC |b|< |a|
|b| >|a|
|
A13)
X(z) = A + B Z (1-1/2z-1) (1 – ¼ z-1)
By solving A= 1 and B=-1
Therefore,
X(z) = z - z z-1/2 z-1/4
x(n) = (1/2) n u(n) – (1/4) n u(n)
|