undefined | unit 3 discrete fourier transform - Goseeko

Back to Study material

DSP

Unit-3Discrete Fourier Transform Q1) Draw block diagram for the function using parallel form H(z)=

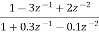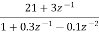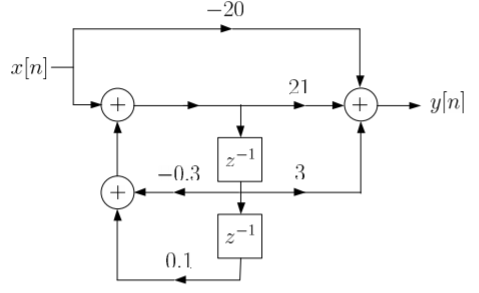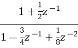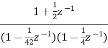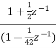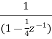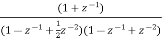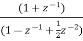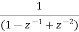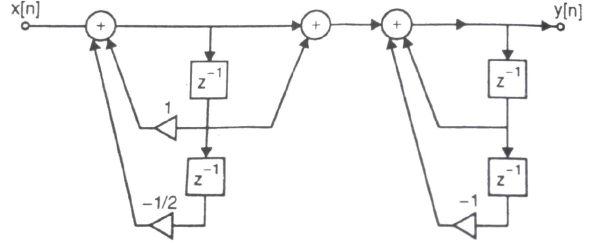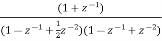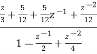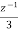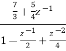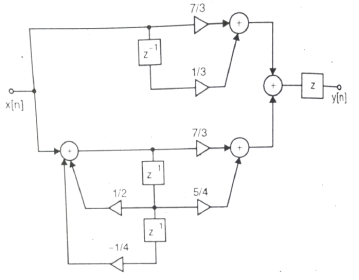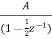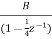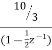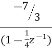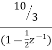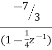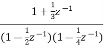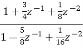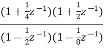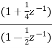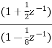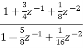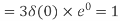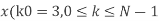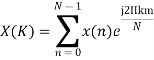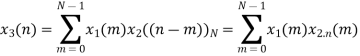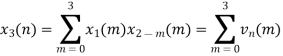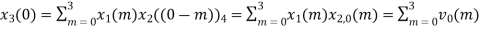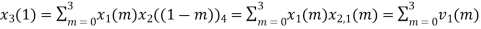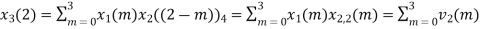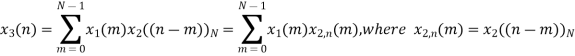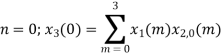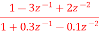
A1)

H(z)=

Writing above transfer function in standard form for parallel realisation we get

H(z)=-20+

The structure is shown below

Fig 1 Parallel Realisation of H(z)=

Q2) For the following LTI system H(z)=

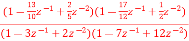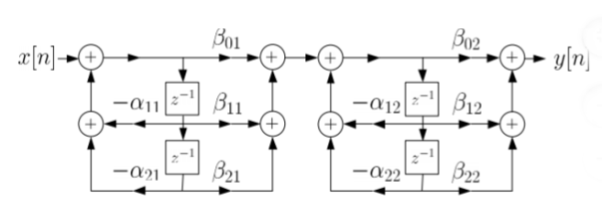
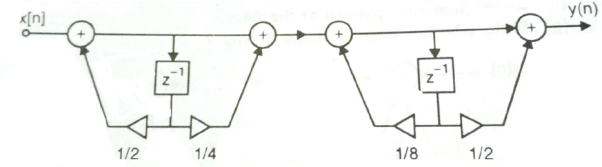
. Realise the cascade form IIR filter.

A2) H(z)=

The above function can be simplified as

H(z)=

Fig 2 Cascade IIR Form

Hence, using the above structure and placing the values of …. And similarly,

Q3) For the system given y(n) -

y(n-1) +

y(n-2) = x(n) +

x(n-1) realise using cascade form?

A3) The system transfer function is given as

H(z) = Y(z)/X(z)

Taking z transform of y(n) -y(n-1) + y(n-2) = x(n) + x(n-1)

Y(z) - z-1Y(z) + z-2 Y(z) = X(z) + z-1 X(z)

H(z)=

Again, simplifying the above function to get into standard cascade form we ca write

H(z) =

= H1(z)+H2(z)

H1(z)=

H2(z)=

The final structure is shown below

Fig 3 Cascade Form of H(z) =

Q4) For the following LTI system H(z)=

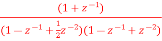. Realise the cascade form?

A4) H(z)=

Writing the above in standard form for cascade realisation

H1(z)=

H2(z)=

The cascade structure is shown below

Fig 4 Cascade Form of H(z)=

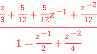
Q5) Realize the system transfer function using parallel structure H(z)=

A5) H(z)=

Taking Z common and then dividing the above function to convert it into standard form for parallel realisation we get

H(z)=Z [ ++]

The parallel structure is shown below

Fig 5 Parallel Realisation of H(z)=

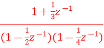
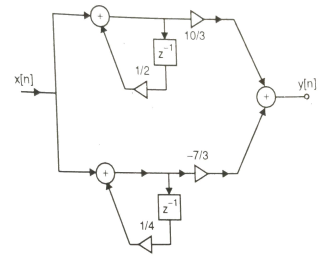
Q6) Realize the system transfer function using parallel structure H(z)=

A6) Converting the above function to standard form using partial fraction technique

H(z)= +

Solving for A and B we get

A= 10/3

B= -7/3

H(z) = +

H1(z) =

H2(z) =

The parallel form realisation is shown below

Fig 6 Parallel Realisation of H(z)=

Q7) For the transfer function H(z) =

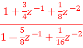. Realise using cascade form?

A7) H(z) =

Writing in standard form

H(z) =

H1(z) =

H2(z) =

The cascade structure is shown below

Fig 7 Cascade Form of H(z) =

Q8) Compute the N-point DFT of x(n)=3δ(n).

A8)

Q9) Compute the N-point DFT of x(n)=7(n−n0)

A9) We know that,

Substituting the value of x(n),

Q10) Perform circular convolution of the two sequences, x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}

A10)

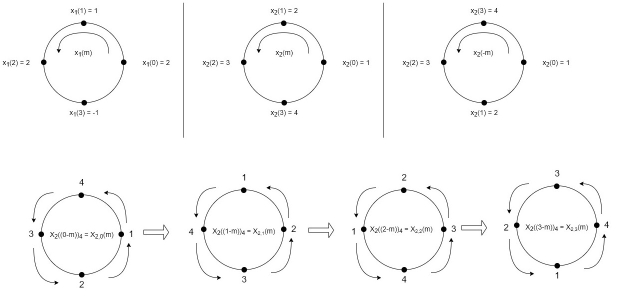
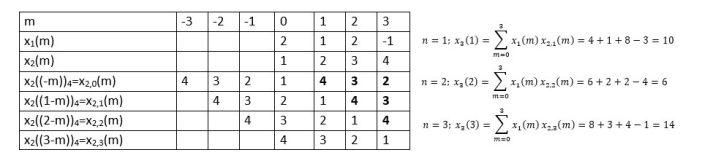
Fig 1 Circular Convolution of x1(n)= {2,1,2,-1} and x2(n)= {1,2,3,4}

(2)

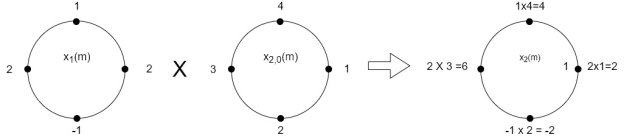
When n=0;

The sum of samples of v0(m) gives x3(0)

⸫ x3(0)=2+4+6-2=10

When n=1;

The sum of samples of v1(m) gives x2(1)

⸫ x3(1)=4 + 1 +8-3=10

(3)When n=2;

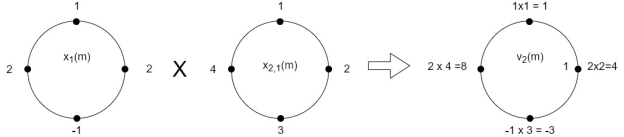
The sum of samples of v2(m) gives x3(2)

⸫ x3(2)=6+2+2-4=6

(4) When n=3;

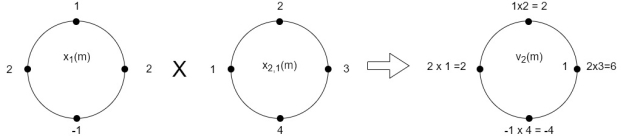
The sum of samples of v3(m) gives x3(3)

⸫ x3(3)=8+ 3+ 4-1= 14

x3(n)={10,10,6,14}

= x1(0) x x2,0(0) + x1(1) x2,0(1) + x1(2) x2,0(2) + x1(3) x2,0(3)

= 2 x 1 + 1 x 4 + 2 x 3 + (-1) x 2 = 2 +4 +6 -2 =10