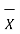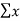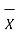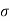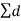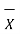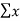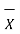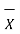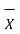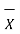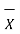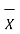Where
x1,x2……xn = readings or variates or samples n = number or readings. |
S.D = |
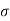 while if it less than 20 the symbol used is s. The Standard deviation of finite number of data is given by:
while if it less than 20 the symbol used is s. The Standard deviation of finite number of data is given by:s = √d1 2 + d2 2 + d3 2 + ………………… + dn2 / n-1 = √ d2 / n-1 |
(a) Arithmetic mean
(b) Deviations : d1 = x1 - d2 = x2 - d3 = x3 - d4 = x4 – d5 = x5 - d6 = x6 - ( c ) Average deviation = D = 0.283 A ( d ) Standard deviation S = √ S=0.399 A |
|
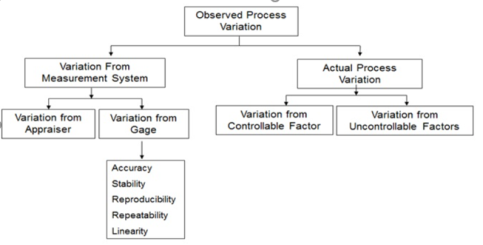
Figure 2. Six Sigma Process Variation
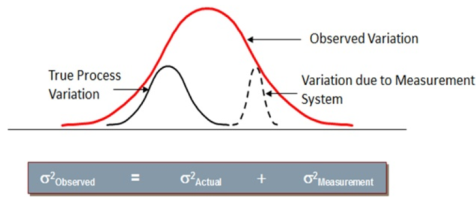
Figure 3. Observed Variation vs True Variation |
Cpk= Process Capability Index. Adjustment of Cp for the effect of non-centered distribution.Cpk is an index which measures how close a process is running to its specification limits, relative to the natural variability of the process. The larger the index, the less likely it is that any item will be outside the specs.” Q7) Determine the mean for the data values 5, 3,7, 8, 4, 9.A7):
Given data values are 5, 3, 7, 8, 4, 9. We know that the procedure to calculate the mean deviation. First, find the mean for the given data: Mean, µ = ( 5+3+7+8+4+9)/6 µ = 36/6 µ = 6 Therefore, the mean value is 6. |
A9)
|