For a balanced condition we can write | unit 5 measurements of r l and c

Back to Study material

Unit 5Measurements of R,L and CQ1) What is a Wheatstone bridge?A1) Wheatstone bridge is an important device used in the measurement of medium resistances. It has four resistive arms, consisting of resistances P, Q R and S together with a source of emf that is battery and null detector galvanometer G or another sensitive current meter. The current through the galvanometer depends on the potential difference between points c and d. The bridge is said to be balanced when there is no current through the galvanometer or when the potential difference across galvanometer is zero. Q2) Explain the working of Wheatstone’s bridge?A2) The balanced condition occurs when voltage from point b to point ‘a’ equal to voltage from point ‘d’ to point ‘b’ or by referring to the other battery terminal when the voltage from point ‘d’ to point ‘c’ equals the voltage from point ‘b’ to point ‘c’.

Figure 1. Wheatstone bridge for measurement of medium resistance.

For a balanced condition, we can write,

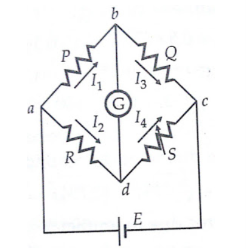
I1 P = I2 R ---------------------(1)

For the galvanometer current to be zero, the following conditions also exist:

I1 = I3 = E/P+Q-----------------------------(2)

I2 = I4 = E/R+S ---------------------------------(3)
where E = emf of the battery

Combining the above three equations we get,

P/P+Q = R/R+S --------------------------------(4)

from which Q.R = P.S ----------------------------------------------------------------(5)
If three resistance are known, the unknown resistance can be obtained by

R = S*(P/Q)

where R is the unknown resistance, S is called the 'standard arm' of the bridge and P and Q are called the 'ratio arms'.Q3)

The following unbalanced Wheatstone Bridge is constructed. Calculate the output voltage across points C and D and the value of resistor R4 required to balance the bridge circuit.

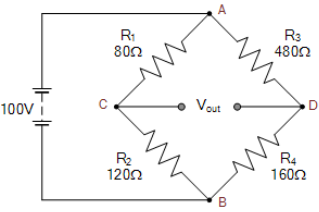
wheatstone bridge example

For the first series arm, ACB

Vc = R2/(R1+R2) x Vs

Vc = 120Ω/ 80Ω + 120 Ω x 100 = 60 volts

For the second series arm, ADB

VD = R4/(R3+R4) x Vs

VD = 160Ω/ 480Ω + 160Ω x 100 = 25 volts

The voltage across points C-D is given as:

Vout = VC – VD

Vout = 60 -25 = 35 volts

The value of resistor, R4 required to balance the bridge is given as:

R4 = R2R3/R1 = 120Ω x 480Ω/80Ω = 720 Ω

Q4) A Wheatstone bridge is used for measuring the value of change of resistance of a strain gauge which forms one of the arms of the bridge. All the arms of the bridge including the strain gauge have a resistance of 100 Ω each. The maximum allowable power dissipation from the strain gauge is 250mW. Determine the value of maximum permissible current through the strain gauge and maximum allowable value of bridge supply voltage. Suppose a source of 20V is available find the value of series resistance to be connected between the source and the bridge to limit the input voltage of the bridge to permissible level.A4)The resistance of strain gauge R = 100Ω. Suppose I is the current through each arm under balanced conditions I 2 R = P where P = power dissipation Hence maximum permissible current =

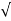P/R =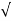

250 x 10 -3 /100 = 0.05A = 50 mA. The maximum allowable voltage which can be applied to the bridge = 2 x 50 x 10 -3 x 100 = 10VVoltage across the series resistor = 20 – 10 = 10V Current through the series resistor = 2 x 50 x 10 -3 x 100 x 10 -3 Resistance of series resistor Rs = 10/100 x 10 -3 = 100ΩQ5) Explain Maxwells bridge?

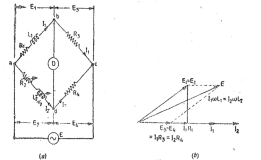
A5) Thes bridge circuit measure an inductance by comparison with a variable standard self-inductance. The connections and the phasor diagrams for balance conditions are shown in Fig. Let Li =unknown inductance of resistance Ri,L2=variable inductance of fixed resistance r2, Ra=variable resistance connected in series with inductor L2, and R3,R4=known non-inductive resistances .

Figure 2. Maxwells Inductance BridgeAt balance

L1 = R3/R4 L2

R1 = R3/R4 (R2+r2)

Q6) Explain capacitance bridge?

Figure 3. Schering Bridge (low voltage)A6) Let C1 = capacitor whose capacitance is to be determined r1 = series resistance representing the loss in the capacitor C1. C2 = standard capacitor. R3 = non-inductive resistance C4 = variable capacitor R4 = variable non-inductive resistance in parallel with variable capacitor C4.

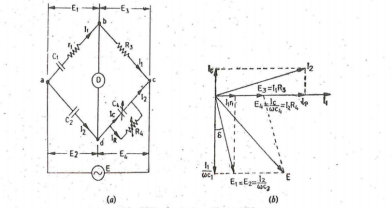
At Balance

(r1+1/jwC1) (R4/ 1+jwC4R4) = 1/jwC2. R3

( r1 + 1/jwC1) R4 = R3 / jwC2 (1+jwC4R4)

r1R4 – jR4/wC1 = -jR3/wC2 + R3R4C4/ C2

Equating real and imaginary terms we obtain r1 = C4/C5 xR3

And C1 = R4/R3 x C2

Two independent balance equations are obtained if C4 and R4 are chosen as the variable elements

Dissipation factor D1 = tan ɸ = w C1 r1 = w . R4/R3 . C2 . C4/C2 . R3 = wC4R4

Q7) What are the advantages of AC bridges ?A7) A.C. bridges form the most convenient method of measuring effective resistance, self-inductance, mutual inductance, capacitance, and other associated quantities such as the Q-factor of coils and loss angles of capacitors at frequencies up to the lower radio-frequency range.Q8) What are the advantages of Maxwells bridge?A8)

The frequency does not appear in the final expression of both equations; hence it is independent of frequency.

Maxwell's inductor capacitance bridge is very useful for the wide range of measurement of inductor at audio frequencies.

Q9) What are the advantages of Wheatstone’s bridge?A9) The main advantage of the Wheatstone bridge is that it can be easily interfaced into various combinations. The Wheatstone bridge is traditionally called ohmmeter as the results are measured in terms of resistance and also are accurate and precise.Q10) What are the applications of bridge circuits?A10) The basic applications of a bridge circuits are instrumentation and as signal rectifiers. Advanced applications would be like for DC motor control or as envelope detectors in receivers with amplitude modulation, where information lies in the envelope. But in any circuit topology you have to generalize the idea behind it. For example, in the bridge circuit's case, the idea is to use the difference potential across the bridge points or the difference current flowing through the bridge, for getting output.

Sign Up