undefined | unit 2 resistance

EEM

Unit- 2ResistanceQ1) Explain the measurement of low resistance?A1) Measurement of Low Resistance by Kelvins Double Bridge.The ratio of the arms p and q are used to connect the galvanometer at the right place between the point j and k. The j and k are used to reduce the effect of connecting lead. The P and Q is the first ratio of the arm and p and q is the second arm ratio.

Figure . Kelvins Double BridgeThe galvanometer is connected between the arms p and q at a point d. The point d places at the centre of the resistance r between the point m and n for removing the effect of the connecting lead resistance which is placed between R the unknown resistance and S the standard resistance S.The ratio of p/q is made equal to P/Q. Under balance condition zero current flows through the galvanometer. The potential difference between the point a and b is equivalent to the voltage drop between the points Eamd.Eab = P/P+Q . Eac Eac= I[ R + S + (p+q)r/p+q+r] -----------------------------(1)Eamd = I[ R + p/(p+q) {(p+q)r/ p+q+r}]Eac = I[ pr/p+q+r] ------------------------------------------(2)Now,For zero galvanometer deflection, Eac = Eamd

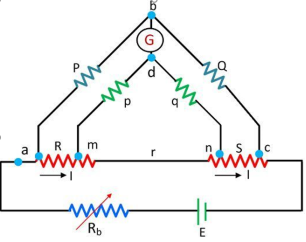
P/P+Q. I[ R + p/(p+q) { (p+q)r/ p+q+r}] = I[pr/p+q+r]

R= P/Q.S + pr/p+q+r[ P/Q -p/q]

As we known, P/Q = p/q then above equation becomes

R=P/Q.S

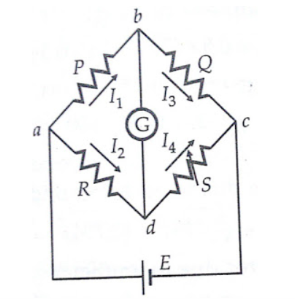
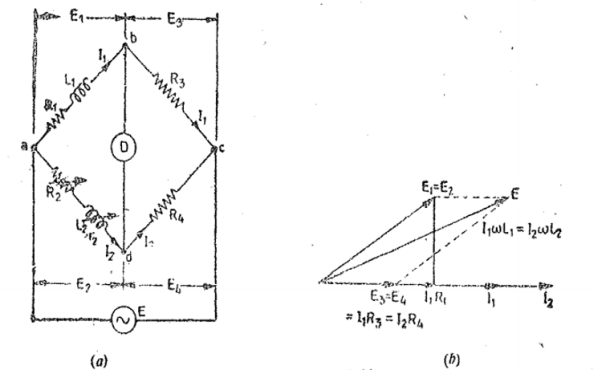
The equation shows that the result obtains from the Kelvin double bridge is free from the impact of the connecting lead resistance.Q2) Explain the measurement of medium resistance?A2) Wheatstone bridge is an important device used in the measurement of medium resistances. The figure below shows the basic circuit of a Wheatstone bridge. It has four resistive arms, consisting of resistances P, Q R and S together with a source of emf that is battery and null detector galvanometer G or another sensitive current meter. The current through the galvanometer depends on the potential difference between points c and d.
The bridge is said to be balanced when there is no current through the galvanometer or when the potential difference across galvanometer is zero. The balanced condition occurs when voltage from point b to point a equals to voltage from point d to point b or by referring to the other battery terminal when the voltage from point d to point c equals the voltage from point b to point c.

Figure . Wheatstone bridge for measurement of medium resistance. For a balanced condition, we can write, I1 P = I2 R ---------------------(1) For the galvanometer current to be zero, the following conditions also exist:      I1 = I3 = E/P+Q-----------------------------(2)     I2 = I4 = E/R+S ---------------------------------(3)
where E = emf of the battery
Combining the above three equations we get,   P/P+Q = R/R+S --------------------------------(4)

from which Q.R = P.S ----------------------------------------------------------------(5)

If three resistance are known, the unknown resistance can be obtained by
   R = S*(P/Q)
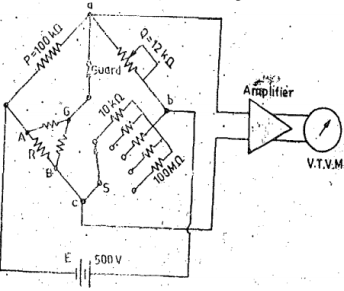
    Q3) Explain the measurement of high resistance?A3) Megohm Bridge Method:

Figure . Megaohm BridgeFigure3. shows the circuit of Megaohm bridge which includes power supplies, bridge members, amplifiers and indicating instrument. It has the range form 0.1MΩ to 10 6 MΩSensitivity for balancing against high resistance is obtained by use of adjustable high voltage supplies of 500V or 1000V and the use of null indicating arrangement such as high gain amplifier with vacuum tube or transistor voltmeter or cathode ray oscilloscope. Since the unknown resistance R=PS/Q , the arm Q is made tampered so that the dial calibration is approximately logarithmic in main decade 1-10, Arm S gives5 multipliers 0.1,1,10,100 and 1000. The junction of ratio arms P and Q is brought on the main panel and is designated as “guard terminal”. Q4)Explain the measurement of resistance by using Wenner method ?A4)Four Point Method (Wenner Method)

Figure. Four Point Earth resistance Testing Method

Press START and read out the resistance value. This is the actual value of the ground Resistance of the electrode under test.

Record the reading on Field Sheet at the appropriate location. If the reading is not stable or displays an error indication, double check the connections. For some meters, the RANGE and TEST CURRENT settings may be changed until a combination that provides a stable reading without error indications is reached.

The Earthing Tester has basically Constant Current generator which injects current into the earth between the two current terminals C1 (E) and C2 (H).

The potential probes P1 & P2 detect the voltage ΔV due to the current injected in the earth by the current terminals C1 & C2.

The test set measures both the current and the voltage and internally calculates and then displays the resistance. R=V/I

If this ground electrode is in parallel or series with other ground rods, the resistance value is the total value of all resistances.

Ground resistance measurements are often corrupted by the existence of ground currents and their harmonics.

To prevent this use Automatic Frequency Control (AFC) System. This automatically that selects the testing frequency with the least amount of noise enabling you to get a clear reading.

Repeat above steps by increasing spacing between each electrode at equal distance and measure earth resistance value.

Average all readings

Q5)Explain the measurement of self- inductance?A5) Measurement of self-inductance by Ammeter and Voltmeter.

Figure. Diagram of the measurement of inductance by the “voltmeter-ammeter” method:(A) ammeter, (V) voltmeter.The “voltmeter-ammeter” method as shown in Figure is used for measuring relatively large inductances (from 0.1 to 1,000 henrys [H]) when the resistance of the windings is significantly lower than the inductance. Here Lx = U/(π f · I) where U is the voltage, I is the current in the circuit whose inductance is being measured, and f is the frequency of the alternating current, usually 50 hertz (Hz). Such inductance meters have an error of 2–3 percent.An AC measuring bridge for frequencies of 100, 400, and 1,000 Hz with standard capacitance or, much less frequently ,standard inductance as shown in figure Figure 2 is the main component of inductance meters. When the bridge is balanced, rx = (R1· R2)/R3Lx = Cs· R1· R2 where rx is the ohmic resistance of the wire of the inductance coil winding. Bridge measurement methods have an error of 1–3 percent; the range of measurement is 0.1 to 1,000 H.

Figure. Diagram of resonance method of inductance measurement: (Lc) coupling loop, (Lx) inductance being measured, (Cc) self-capacitance of coil, (Cs) standard capacitance. Working of Maxwell’s Bridge. This bridge circuit measures an inductance by comparison with a variable standard self-inductance. The connections and the phasor diagrams for balance conditions are shown in Fig. Let Li =unknown inductance of resistance Ri,L2=variable inductance of fixed resistance r2, Ra=variable resistance connected in series with inductor L2, and R3,R4=known non-inductive resistances .

Figure. Maxwells Inductance BridgeAt balance L1 = R3/R4 L2 R1 = R3/R4 (R2+r2)Q6)Explain the working of Hays Bridge?A6) The Hay's bridge is a modification of Maxwell's bridge. The block diagram and the phasor diagram for this bridge are shown in Figure. The bridge uses a resistance in series with the standard capacitor.

Figure.Hays BridgeLet L1 =unknown inductance having a resistance Ri, R2, Ra.R4=known non-inductive resistances, and C4=standard capacitor. At balance, (R1+jwL1)(R4-jwC4) = R1R3 or R1R2+L1/C4+jwL1R4-jR1/wC4=R2R3Separating the real and imaginary terms we obtain

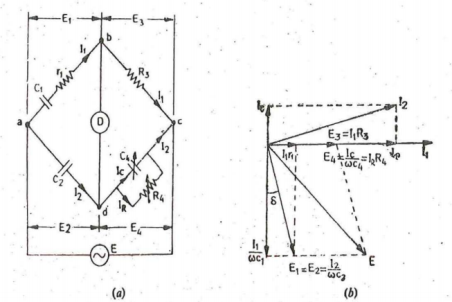
R1R4+L1/C4=R2R3 and L1 =R1/w 2 R4C4

Solving the two equations we have L1 = R2R3C4/1+w 2 C42 R4 2 ---------------(1)

R1 = w 2 R2 R3 R4 C4 2/ 1+ w 2 c4 2 R4 2 ----------------------------------------------(2)

The Q factor of the coil is Q=wL1/R1 = 1/wC4R4-------------------------------------(3)

Q7) Explain the measurement of mutual inductance?A7) Mutual inductance is measured by using standard of comparison a mutual inductance, a self-inductance, or capacitance. When the standard mutual inductance is continuously variable and of such a range that it can be made equal to the unknown mutual inductance, the Felici mutual-inductance balance is the simplest method.

Measurement Small Inductances

Figure . Felici mutual-inductance balanceIn Figure the primaries of both mutual inductances, unknown and standard, are connected in series to a power source. Their secondaries are also connected in series to a suitable detector, head telephones, or oilier a-c operated meter, in such direction that their induced voltages oppose. The standard is then varied until a balance is obtained.The error in this measurement is essentially that of the standard, provided that the capacitive reactance’s between the coils of the mutual inductances are large compared with their mutual reactance’s and that the impedance of the detector is small.Q8)Explain the working of Schering Bridge ?A8)

Figure . Schering Bridge The connection and phasor diagram of the bridge under balance conditions are shown in figure. Let C1 = capacitor whose capacitance is to be determined r 1 = series resistance representing the loss in capacitor C1 C2 = standard capacitor. R3 = non-inductive resistance C4= variable capacitor R4 = variable non-inductive resistance in parallel with variable capacitor C4. At balance

(r1+1/jwC1)(R4/1+jwC4R4) = 1/jwC2.R

(r1+1/jwC1) R4 = R3/jwC2(1+jwC4R4)

r 1 R4 -jR4/wC1=-j R3/wC2+R3R4C4/C2

Equating real and imaginary terms we obtain

r 1 = C4/C3 .R3

C1 = R4/R3. C2

Two independent balance equations are obtained if C4 and R4 are chosen as the variable elements.

Dissipation factor D1 =tan ɸ=wC1r1=w.R4/R3 .C2.C4/C2 .R3 = wC4 R4

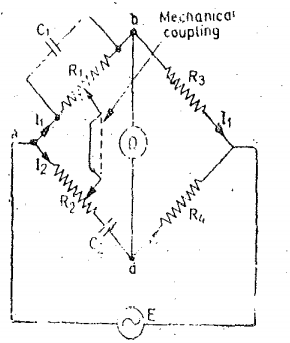
Q9)Explain the working of Weins bridge?A9) Weins bridge is primarily used to determine the frequency not only for AC bridge but for other circuits.

Figure. Weins bridge

At balance (R1/1+jwC1R1) R4 = (R2-j/wC2) R3

R4/R3 = R3/R1 + C1/C2 + j(wC1R2 -1/wC2R1)

Equating real and imaginary terms we get

R4/R3 = R2/R1 +C1/C2

And wC1R2 -1/wC2R1 =0 from which w=1/√R1R2C1C2 and

Frequency f =1/2π√R1R2C1C2 .

In most Wein bridge the components are chosen such that

R1=R2=R and C1=C2=C

Therefore R4/R3 = 2

F=1/2πRC

Q10)Explain Wagner Earthing Device?A10)

Figure. Wagner Earthing deviceFigure shows the connections of the device for use in conjunction with the general form of bridge network, in which Z1, Z2, Za and Z4 are the impedances of the bridge arms. Z5 and Z6 are the two variable impedances of the Wagner earth branch, the centre point of which is earthed as shown. · These impedances may consist of variable resistances and capacitances like those used in the arms. of the bridge proper · The two impedances Z5 and Z6 must be capable of forming a balanced bridge with Z1 and Za or Z2 and Z4 and can be a duplicate of either pair of arms C1,C2, C3 and C4 are the stray earth capacitances appearing at the apexes of the bridge and D is the detector. If tile switch S is on contact d, balance of the bridge may be obtained by adjustment of the impedances Z2 and Z4. The presence of the earth capacitances will prevent true balance being obtained, but a point of minimum sound can be obtained.

Sign Up