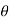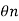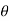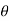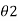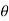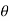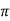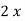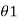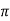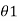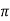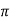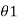EEM
UNIT-3 Galvanometer Q1)Explain the construction of D'Arsonval Galvanometer?A1)
|
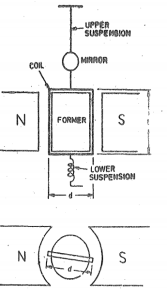
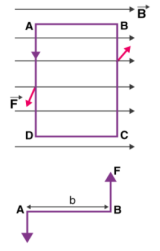
Figure d’Arsonval GalvanometerThe construction of galvanometer consists of Moving coil: It is the current carrying element. It is either rectangular or circular in shape and consists of several turns of fine wire. This coil is suspended so that it is free to tum about its vertical axis of symmetry. It is arranged in uniform, radial, horizontal magnetic field in the air gap between pole pieces and armature (iron core) of a permanent magnet. The armature (iron core) is spherical in shape if the coil is circular but is cylindrical if the coil is rectangular. 2. Damping There is a damping torque present owing to production of eddy currents in the metal former on which the coil is mounted. Damping is also obtained by connecting a low resistance across the galvanometer terminals. 3. Suspension The coil is supported by a fiat ribbon suspension which also carries current to the coil. The other current connection in a sensitive galvanometer is a coiled wire. This is called the lower suspension and has a negligible torque effect. This type of galvanometer must be levelled carefully so that the coil hangs straight and centrally without rubbing the poles or the soft iron cylinder. 4. Indication. The suspension carries a small mirror upon which a beam of light is cast. The beam of light is reflected on to a scale upon which the deflection is measured. This scale is usually about 1 metre away from the instrument, although 1 /2 metre may be used for greater compactness.Q2)Explain the working and principle of operation?A2)Let a current I flow through the rectangular coil of n number of turns and a cross-sectional area A. When this coil is placed in a uniform radial magnetic field B, the coil experiences a torque τ.Initially consider a single turn ABCD of the rectangular coil having a length l and breadth b. This is suspended in a magnetic field of strength B such that the plane of the coil is parallel to the magnetic field.Since the sides AB and DC are parallel to the direction of the magnetic field, they do not experience any effective force due to the magnetic field. The sides AD and BC being perpendicular to the direction of field experience an effective force F given by F=BI.l
Figure Current carrying loop in magnetic field. We know that torque τ = force x perpendicular distance between the forcesτ = F × bSubstituting the value of F we already know,Torque τ acting on single-loop ABCD of the coil = BIl × bWhere lx b is the area A of the coil,Hence the torque acting on n turns of the coil is given byτ = nIABThe magnetic torque thus produced causes the coil to rotate, and the phosphor bronze strip twists. In turn, the spring S attached to the coil produces a counter torque or restoring torque kθ which results in a steady angular deflection.Under equilibrium condition:kθ = nIABHere k is called the torsional constant of the spring (restoring couple per unit twist). The deflection or twist θ is measured as the value indicated on a scale by a pointer which is connected to the suspension wire.θ= ( nAB / k)ITherefore θ ∝ IQ3)Briefly describe the working of ballistic galvanometer?A3) Let us consider a rectangular-shaped coil consists of ‘N’ number of turns kept in a constant magnetic field. The length and breadth are ‘l’ and ‘b’. So, the area of the coil isA = l × bWhen current flows across the coil, then the torque is developed . The magnitude of the torque is given by τ = NiBAAssume that the flow of current across the coil for each minimal time is dt and so the change in current is represented asτ dt = NiBA dtWhen there is current flow across the coil for a time of ‘t’ seconds, then the value is represented asʃ0t τ dt = NBA ʃ0t idt = NBAqwhere ‘q’ is the total amount of charge that flows across the coil. The inertial moment that exists for the coil is shown as ‘I’ and the coil’s angular velocity is shown as ‘ω’. The below expression provides the angular momentum of the coil and it is lω. It is like the pressure that is applied to the coil. By multiplying the above two equations, we getlw = NBAqAlso, the kinetic energy across the coil will have deflection at ‘ϴ’ angle and the deflection will be restored using the spring. It is represented byRestoring torque value = (1/2)cϴ2Kinetic energy value = (1/2)lw2As the coil’s restoring torque is similar to the deflection then(1/2)cϴ2 = (1/2)lw2cϴ2 = lw2Also, the periodic oscillations of the coil is shown as belowT = 2π√(l/c) T2 = (4π2l/c)(T2/4π2) = (l/c)(cT2/4π2) = lFinally, (ctϴ/2π) =lw = NBAqq = (ctϴ)/NBA2πq = [(ct)/NBA2π] * ϴ)Assume that k = [(ct)/NBA2πThen q = k ϴSo, ‘k’ is the constant term of the ballistic galvanometer.Q4)Explain the deflection of ballistic galvanometer?
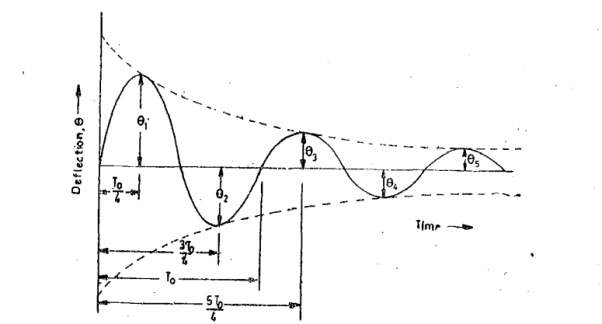
Variation of deflection of ballistic galvanometerLogarithmic decrement λ = π 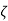 td/To For cases where damping is small Td =To and λ = πζπ D/Do = π D/2√KJ Hence the equation is given by
td/To For cases where damping is small Td =To and λ = πζπ D/Do = π D/2√KJ Hence the equation is given by 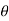 1 =
1 = 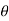 e - λ/2 -------------------------------------(1)Hence
e - λ/2 -------------------------------------(1)Hence 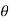 2 =
2 = 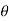 Q e -3λ/2 -------------------------------------(2)
Q e -3λ/2 -------------------------------------(2)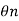 =
=  –(2n-1)λ/2 -----------------------------------------(3)Let us examine the case when the galvanometer is free from damping that is D=0 . The equation of motion of undamped galvanometer is derived as
–(2n-1)λ/2 -----------------------------------------(3)Let us examine the case when the galvanometer is free from damping that is D=0 . The equation of motion of undamped galvanometer is derived as 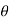 =AQ sin 2π/To .t --------------------------------------------(4)Amplitude of swings of undamped oscillations is given by
=AQ sin 2π/To .t --------------------------------------------(4)Amplitude of swings of undamped oscillations is given by  o = AQ sin 2π/To . To/4 = AQ Hence we write
o = AQ sin 2π/To . To/4 = AQ Hence we write 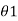 =
= 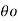 e -λ/2
e -λ/2 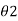 =
= 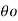 e -3λ/2
e -3λ/2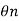 =
= 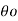 e–(2n-1)λ/2 Logarithmic decrement is logarithm of ratio of successive swings. Logarithmic decrement λ = log (
e–(2n-1)λ/2 Logarithmic decrement is logarithm of ratio of successive swings. Logarithmic decrement λ = log (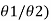 Now the ratio of successive swings is :
Now the ratio of successive swings is : 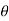 1/
1/ 2 = e -λ/2 / e -3λ/2 = e λ Similarly
2 = e -λ/2 / e -3λ/2 = e λ Similarly 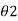 /
/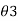 = e λ
= e λ
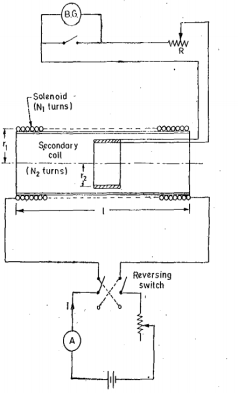
Q5)Write a short note on calibration of galvanometer?A5)
Calibration of galvanometer with mutual inductanceUsing Mutual Inductance:The mutual inductance is usually in the form of standard solenoid with secondary coil. A standard solenoid consists of long coil wound on a cylinder. The length of the cylinder is large as compared with its diameter. At the centre of solenoid, a secondary coil is placed. The axial length of the secondary coil is small. The secondary coil is connected to the ballistic galvanometer. When a current is passed through solenoid the field strength at the centre is H = N1I/l cos 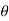 = N1 I / l . l/2 / √ (l/2) 2 + (r1) 2 Where N1 = number of turns of the solenoid I = current through the solenoid l=length of the solenoid r1 = mean radius of the solenoid. Flux density at the centre of solenoid B =
= N1 I / l . l/2 / √ (l/2) 2 + (r1) 2 Where N1 = number of turns of the solenoid I = current through the solenoid l=length of the solenoid r1 = mean radius of the solenoid. Flux density at the centre of solenoid B =  H Flux linking with secondary coil ɸ = B x area of secondary coil = B x π r 2 =
H Flux linking with secondary coil ɸ = B x area of secondary coil = B x π r 2 = 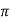 Br2 2 = π μo H r2 Where r2 = mean radius of secondary coil. Let N2 be the number of turns in the secondary coil. Therefore, flux linkages of secondary coil ɸ2 = N2 ɸ = 2 πμoN2Hr2 2 Suppose
Br2 2 = π μo H r2 Where r2 = mean radius of secondary coil. Let N2 be the number of turns in the secondary coil. Therefore, flux linkages of secondary coil ɸ2 = N2 ɸ = 2 πμoN2Hr2 2 Suppose 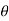 i is the throw of the galvanometer Therefore, constant of galvanometer in terms of flux linkages Kɸ = 2
i is the throw of the galvanometer Therefore, constant of galvanometer in terms of flux linkages Kɸ = 2 μoN2 Hr2 2 /
μoN2 Hr2 2 / 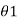 weber turn per radian
weber turn per radian
The equivalent circuit with mutual inductance is given by Kɸ = 2MI/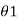 weber turn per radian Suppose the change in flux linkage takes place in time t . Therefore, emf induced in the secondary coil is given by Rate of change in flux linkages = -d
weber turn per radian Suppose the change in flux linkage takes place in time t . Therefore, emf induced in the secondary coil is given by Rate of change in flux linkages = -d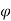 /dt = 2
/dt = 2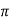 μoN2 Hr2 2 / t This emf sends a current I through the galvanometer i = 2
μoN2 Hr2 2 / t This emf sends a current I through the galvanometer i = 2 μoN2 Hr2 2 /R twhere R is the galvanometer circuit resistance.Charge passing in time t Q=it = 2
μoN2 Hr2 2 /R twhere R is the galvanometer circuit resistance.Charge passing in time t Q=it = 2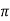 μoN2 Hr2 2 /RBut Q = Kq
μoN2 Hr2 2 /RBut Q = Kq 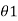 Where kq = constant of galvanometer in coulomb per radian
Where kq = constant of galvanometer in coulomb per radian
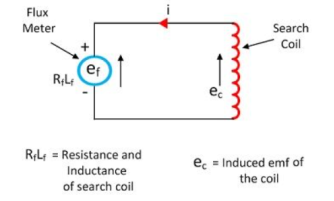
Thus, the galvanometer constant can be obtained in terms of coulomb per radian. Q6)Explain the Measurement of flux and Magnetic field by using Galvanometers ?Magnetic field by Galvanometers A galvanometer is not used to measure a current, but rather to detect whether the current is flowing and in which direction.If we have a small coil of area A, N turns, resistance R, we could place the coil perpendicular to a magnetic field B, and then connect the coil to a ballistic galvanometer. Then, suddenly remove the coil from the so that the flux through the coil goes from AB to zero. While the flux through the coil is changing, and EMF will be induced, equal to NAB and consequently a current will flow momentarily through the coil of magnitudeI = NAB/R+r’ where r is the resistance of the galvanometer. Integrate this with respect to time with initial condition Q=0 when t=0 and we find the total quantity of electricity that flows through the galvanometer Q = N AB / R + r’ Since Q can be measured from the amplitude of the galvanometer motion , the strength of the magnetic field B is determined. Measurement of flux by GalvanometersThe fluxmeter is the advanced form of the ballistic galvanometer which has advantages like the meter which has low controlling torque and heavy electromagnetic damping.
Figure. Flux meterThe terminals of the fluxmeter are connected across the search coil as shown in the figure below. The flux linking with the coil is varied by either removing it from the magnetic field or by reversing the field of the magnet. The change of the flux induces the electromotive force in the coil. This emf induces the current in the search coil and sends it through the flux meter. Because of the current, the pointer of the fluxmeter deflects, and their deflection is directly proportional to the change in the value of flux linkages.Q7)Briefly describe Crompton potentiometer?
Figure : Crompton PotentiometerThis potentiometer is provided with a double throw switch which allows the connection of either the standard cell or the unknown emf to be applied to the working circuit. A key and a protective resistance usually about 10 KΩ is used in the galvanometer circuit. To operate the galvanometer at its maximum sensitivity provision is made to short the protective resistance for the balance conditions.Q8)Write a short note on Deflection Potentiometer?A8)
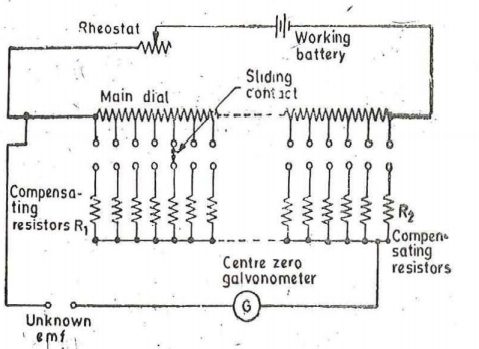
Figure. Deflectional Potentiometer1n this potentiometer only one or two main dials, consisting of decade resistance boxes, are used. A centre zero type galvanometer is included in the circuit to indicate deflection. The galvanometer circuit includes a set of compensating resistors R1, R2. The values of the compensating resistors is such that the resistance of the potentiometer circuit, is viewed from the terminals where the unknown emf is applied, remains constant irrespective of the position of the sliding contacts. This means that current through the galvanometer will always be proportional to the out of balance current whatever may be the setting of the main dials. Thus, the galvanometer scale can be calibrated to read the out of balance emf directly. The value of the · unknown emf is obtained by adding the galvanometer reading to the main dial setting. The main dial setting is kept nearly equal to the emf being measured. The potentiometer is used to monitor the value of temperature where a thermocouple· is employed. The output of the thermocouple is fed to the unknown emf terminals.Q9)Explain the working of Drysdale -Tinsley potentiometer?A9)
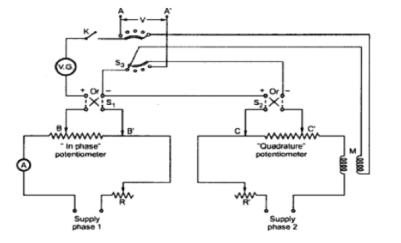
Figure: Drysdale-Tinsley PotentiometersThe working of Drysdale a.c. potentiometer is as under :(1) First, the a.c. potentiometer is standardised which means it is made direct reading. For this purpose, the slide-wire circuit is connected to d.c. supply and the standard current is obtained by using a standard cell. This standard current makes the potentiometer direct reading and is measured by a dynamometer ammeter which is included in the battery supply circuit of the potentiometer. The ammeter remains connected for a. c. operation because the r.m.s. value of current in the slide-wire must be maintained at the same (2) Once the a.c. potentiometer is standardised, the d.c. supply is removed, and the slide-wire is connected to the rotor winding of the phase-shifting circuit. The r.m.s. value of alternating current in the slide-wire is made the same as on the d.c. supply. The Balance is obtained by varying the position of slide-wire contact and position of the phase-shifting rotor. When the vibration galvanometer reads zero, it means that balance is achieved. Now, slidewire reading gives the magnitude r 'of the unknown a.c. voltage and the rotor position its phase angle θ. Therefore, the unknown a.c. voltage is represented as V∠θ.Q10)Explain the working of Gall Tinsley Potentiometer?A10) In Gall-Tinsley Potentiometer the in-phase and quadrature potentiometer consist of sliding contacts BB’ and CC’ respectively. The Rheostat’s r and R’ provide respective potentiometers for the adjustment of current. By using different arrangement, the supply for the potentiometer is obtained. A vibration galvanometer VG is tuned to the supply frequency and connected in series with the switch K and electrodynamometer type ammeter.
Figure: Gall-Tinsley PotentimeterThe emf to be measured is connected across the terminals A-A’ using selector S3. Sliding contects of both potentiometers are adjusted till the contacts of both the potentimeters are adjusted till null deflection is obtained. Under balance condition the in-phase component of the unknown emf is obtained from in-phase potentiometer while the quadrature component of the unknown emf is obtained from quadrature potentiometer. If needed the polarity of the test voltage may be reversed by using sign changing switches S1 and S2 to balance the potentiometer.
|
|
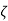 td/To For cases where damping is small Td =To and λ = πζπ D/Do = π D/2√KJ Hence the equation is given by
td/To For cases where damping is small Td =To and λ = πζπ D/Do = π D/2√KJ Hence the equation is given by 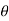 1 =
1 = 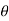 e - λ/2 -------------------------------------(1)Hence
e - λ/2 -------------------------------------(1)Hence 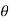 2 =
2 = 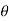 Q e -3λ/2 -------------------------------------(2)
Q e -3λ/2 -------------------------------------(2)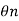 =
=  –(2n-1)λ/2 -----------------------------------------(3)Let us examine the case when the galvanometer is free from damping that is D=0 . The equation of motion of undamped galvanometer is derived as
–(2n-1)λ/2 -----------------------------------------(3)Let us examine the case when the galvanometer is free from damping that is D=0 . The equation of motion of undamped galvanometer is derived as 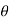 =AQ sin 2π/To .t --------------------------------------------(4)Amplitude of swings of undamped oscillations is given by
=AQ sin 2π/To .t --------------------------------------------(4)Amplitude of swings of undamped oscillations is given by  o = AQ sin 2π/To . To/4 = AQ Hence we write
o = AQ sin 2π/To . To/4 = AQ Hence we write 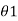 =
= 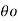 e -λ/2
e -λ/2 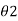 =
= 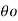 e -3λ/2
e -3λ/2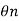 =
= 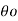 e–(2n-1)λ/2 Logarithmic decrement is logarithm of ratio of successive swings. Logarithmic decrement λ = log (
e–(2n-1)λ/2 Logarithmic decrement is logarithm of ratio of successive swings. Logarithmic decrement λ = log (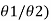 Now the ratio of successive swings is :
Now the ratio of successive swings is : 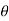 1/
1/ 2 = e -λ/2 / e -3λ/2 = e λ Similarly
2 = e -λ/2 / e -3λ/2 = e λ Similarly 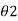 /
/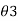 = e λ
= e λ
From the above we get
Logarithmic decrement is λ = 1/n- log e ( |
|
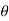 = N1 I / l . l/2 / √ (l/2) 2 + (r1) 2 Where N1 = number of turns of the solenoid I = current through the solenoid l=length of the solenoid r1 = mean radius of the solenoid. Flux density at the centre of solenoid B =
= N1 I / l . l/2 / √ (l/2) 2 + (r1) 2 Where N1 = number of turns of the solenoid I = current through the solenoid l=length of the solenoid r1 = mean radius of the solenoid. Flux density at the centre of solenoid B =  H Flux linking with secondary coil ɸ = B x area of secondary coil = B x π r 2 =
H Flux linking with secondary coil ɸ = B x area of secondary coil = B x π r 2 = 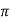 Br2 2 = π μo H r2 Where r2 = mean radius of secondary coil. Let N2 be the number of turns in the secondary coil. Therefore, flux linkages of secondary coil ɸ2 = N2 ɸ = 2 πμoN2Hr2 2 Suppose
Br2 2 = π μo H r2 Where r2 = mean radius of secondary coil. Let N2 be the number of turns in the secondary coil. Therefore, flux linkages of secondary coil ɸ2 = N2 ɸ = 2 πμoN2Hr2 2 Suppose 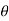 i is the throw of the galvanometer Therefore, constant of galvanometer in terms of flux linkages Kɸ = 2
i is the throw of the galvanometer Therefore, constant of galvanometer in terms of flux linkages Kɸ = 2 μoN2 Hr2 2 /
μoN2 Hr2 2 / 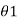 weber turn per radian
weber turn per radian 2 |
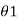 weber turn per radian Suppose the change in flux linkage takes place in time t . Therefore, emf induced in the secondary coil is given by Rate of change in flux linkages = -d
weber turn per radian Suppose the change in flux linkage takes place in time t . Therefore, emf induced in the secondary coil is given by Rate of change in flux linkages = -d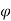 /dt = 2
/dt = 2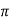 μoN2 Hr2 2 / t This emf sends a current I through the galvanometer i = 2
μoN2 Hr2 2 / t This emf sends a current I through the galvanometer i = 2 μoN2 Hr2 2 /R twhere R is the galvanometer circuit resistance.Charge passing in time t Q=it = 2
μoN2 Hr2 2 /R twhere R is the galvanometer circuit resistance.Charge passing in time t Q=it = 2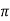 μoN2 Hr2 2 /RBut Q = Kq
μoN2 Hr2 2 /RBut Q = Kq 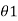 Where kq = constant of galvanometer in coulomb per radian
Where kq = constant of galvanometer in coulomb per radian Kq = Q/ = |
|
|
|
|
|
0 matching results found