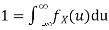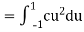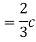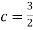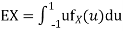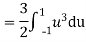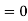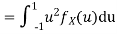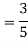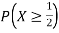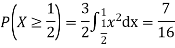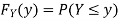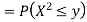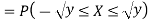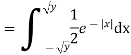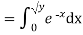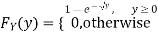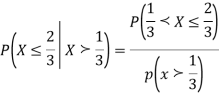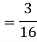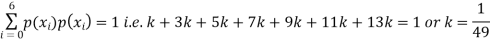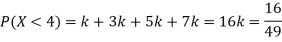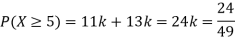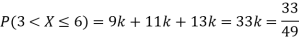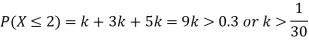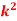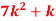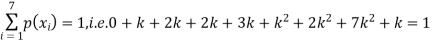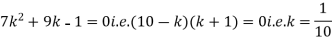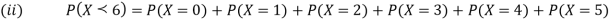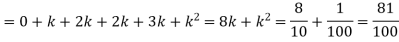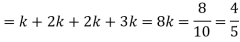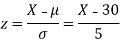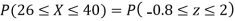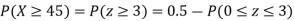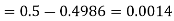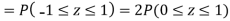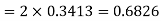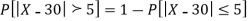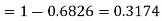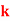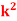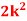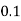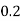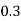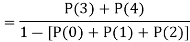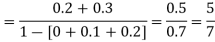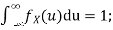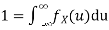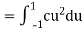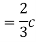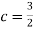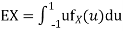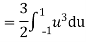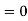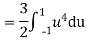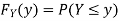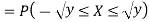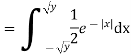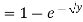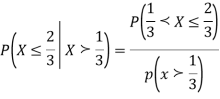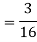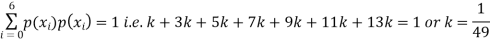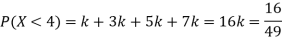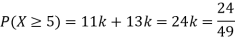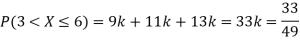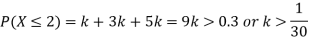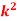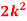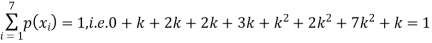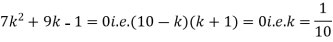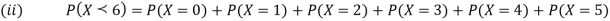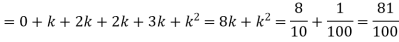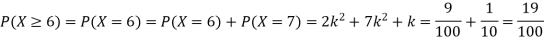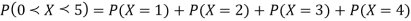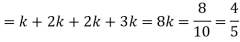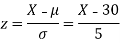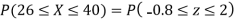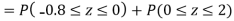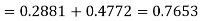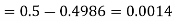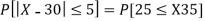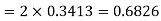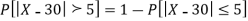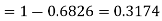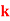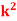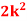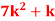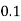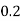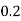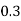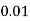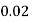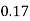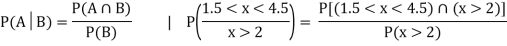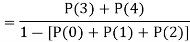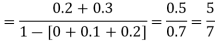Unit-2

Continuous Probability Distributions

Q1) Let X be a random variable with PDF given by

a, Find the constant c.

b. Find EX and Var (X).

c. Find P(X ).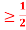

S1)

Q2) Let X be a continuous random variable with PDF given by

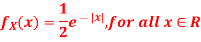
If 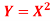, find the CDF of Y.

S2) First we note that , we have

Q3) Let X be a continuous random variable with PDF

Find .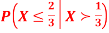

S3) We have

Q4) If a continuous random variable X has the following probability density function:

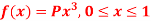
Then find-

1. P[0.2 < X < 0.5]

S4)

Here f(x) is the probability density function, then-

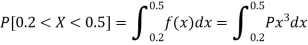
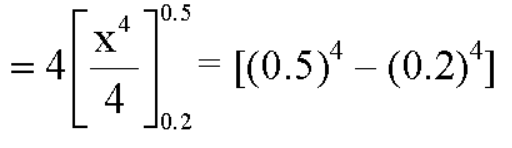
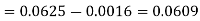
Q5) The probability density function of a variable X is

(i)                Find

(ii)             What will be e minimum value of k so that

S5) (i) If X is a random variable then

Q6) A random variate X has the following probability function

(i)                Find the value of the k.

(ii)            

S6) (i) If X is a random variable then

Q7) X is a normal variate with mean 30 and S.D. 5, find the probabilities that

(i)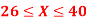               

(ii)            

(iii)          |X-30|≥5

S7) We have μ =30 and 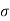=5

Q8) In a test on 2000 electric bulbs, it was found that the life of a particular make was normally distributed with an average life of 2040 hours and standard deviation of 60 hours. Estimated number of bulbs likely to burn for

S8)

Here μ = 2040 hours and 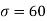hours

(a)  For x = 2150,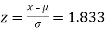

Area against z = 1.83 in the table III = 0.4664

We however require the area to the right of the ordinate at z = 1.83. This area = 0.5-0.4664=0.0336

Thus the number of bulbs expected to burn for more than 2150 hours.

 = 0.0336×2000 = 67 approximately

(b) For x = 1950,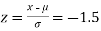

The area required in this case is to be left of z = -1.33

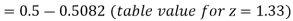
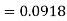
Therefore the number of bulbs expected to burn for less than 1950 hours

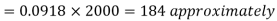
(c)  When x = 1920,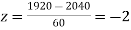

When x = 2160,

The number of bulbs expected to learn for more than 1920 hours but less than 2160 hours will be represented by the area between z = -2 and z = 2. This is twice the area from the table for z =2, i.e. 2 × 0.4772=0.9544

Thus required number of bulbs = 0.9544 × 2000 = 1909 nearly

Q9) Following probability distribution

Find: (i) k   (ii)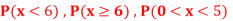

(i)                Distribution function

(ii)             If 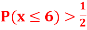  find minimum value of C

(iii)          Find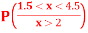

S9)

If P(x) is p.m.f –

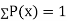
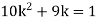
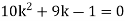
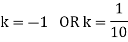
(i)

(ii)

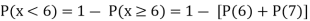
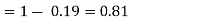
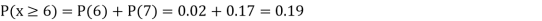
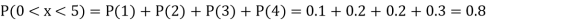
(iii)

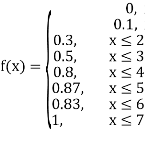
(iv)

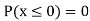
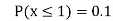
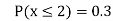
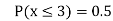
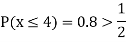
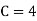
(v)

Q10) I choose real number uniformly at random in the interval [a, b], and call it X. Buy uniformly at random, we mean all intervals in [a, b] that have the same length must have the same probability. Find the CDF of X.

S10)

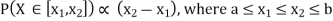
Since 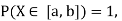we conclude

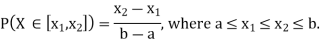
Now, let us find the CDF. By definition 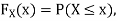thus immediately have

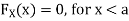
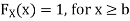
For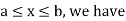

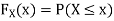
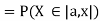
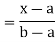
Thus, to summarize

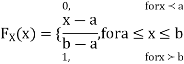
Note that hear it does not matter if we use “<” or “≤” as each individual point has probability zero, so for example 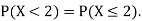Figure 4.1 shows the CDF of X. As we expect the CDF starts at 0 at end at 1.

Unit-2

Continuous Probability Distributions

Q1) Let X be a random variable with PDF given by

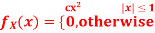
a, Find the constant c.

b. Find EX and Var (X).

c. Find P(X ).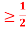

S1)

Q2) Let X be a continuous random variable with PDF given by

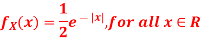
If 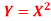, find the CDF of Y.

S2) First we note that 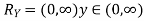, we have

Q3) Let X be a continuous random variable with PDF

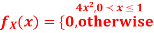
Find .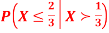

S3) We have

Q4) If a continuous random variable X has the following probability density function:

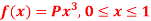
Then find-

1. P[0.2 < X < 0.5]

S4)

Here f(x) is the probability density function, then-

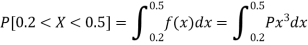
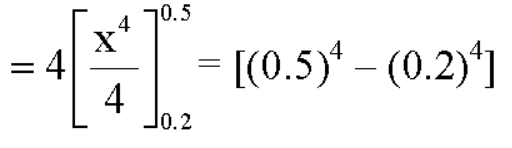
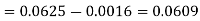
Q5) The probability density function of a variable X is

(i)                Find

(ii)             What will be e minimum value of k so that

S5) (i) If X is a random variable then

Q6) A random variate X has the following probability function

(i)                Find the value of the k.

(ii)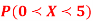            

S6) (i) If X is a random variable then

Q7) X is a normal variate with mean 30 and S.D. 5, find the probabilities that

(i)               

(ii)            

(iii)          |X-30|≥5

S7) We have μ =30 and 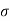=5

Q8) In a test on 2000 electric bulbs, it was found that the life of a particular make was normally distributed with an average life of 2040 hours and standard deviation of 60 hours. Estimated number of bulbs likely to burn for

S8)

Here μ = 2040 hours and 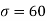hours

(a)  For x = 2150,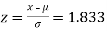

Area against z = 1.83 in the table III = 0.4664

We however require the area to the right of the ordinate at z = 1.83. This area = 0.5-0.4664=0.0336

Thus the number of bulbs expected to burn for more than 2150 hours.

 = 0.0336×2000 = 67 approximately

(b) For x = 1950,

The area required in this case is to be left of z = -1.33

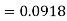
Therefore the number of bulbs expected to burn for less than 1950 hours

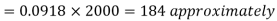
(c)  When x = 1920,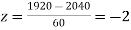

When x = 2160,

The number of bulbs expected to learn for more than 1920 hours but less than 2160 hours will be represented by the area between z = -2 and z = 2. This is twice the area from the table for z =2, i.e. 2 × 0.4772=0.9544

Thus required number of bulbs = 0.9544 × 2000 = 1909 nearly

Q9) Following probability distribution

Find: (i) k   (ii)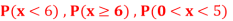

(i)                Distribution function

(ii)             If 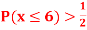  find minimum value of C

(iii)          Find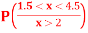

S9)

If P(x) is p.m.f –

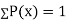
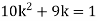
(i)

(ii)

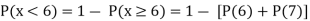
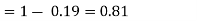
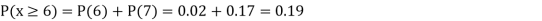
(iii)

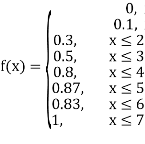
(iv)

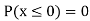
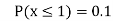
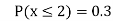
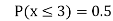
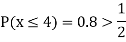
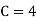
(v)

Q10) I choose real number uniformly at random in the interval [a, b], and call it X. Buy uniformly at random, we mean all intervals in [a, b] that have the same length must have the same probability. Find the CDF of X.

S10)

Since 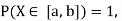we conclude

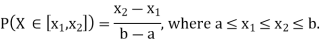
Now, let us find the CDF. By definition 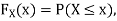thus immediately have

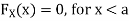
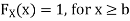
For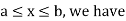

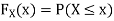
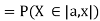
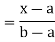
Thus, to summarize

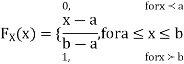
Note that hear it does not matter if we use “<” or “≤” as each individual point has probability zero, so for example 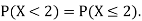Figure 4.1 shows the CDF of X. As we expect the CDF starts at 0 at end at 1.