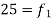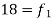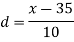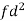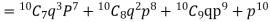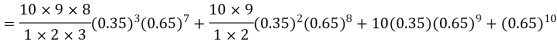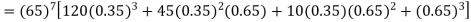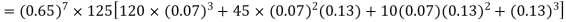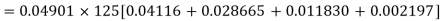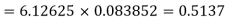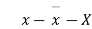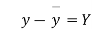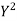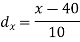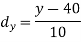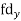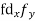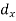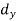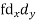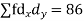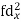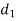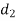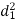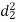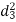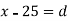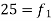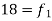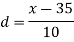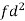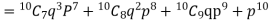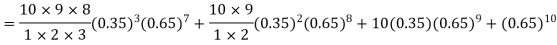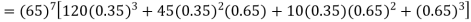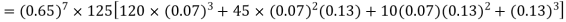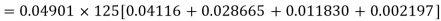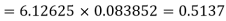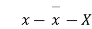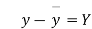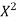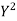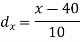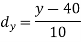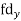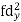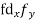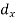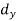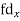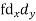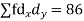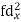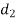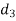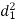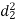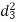Unit-4
Basic Statistics
Q1) Find the arithmetic mean for the following distribution
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
S1) Let assumed mean (a) = 25
Class | Mid-value (x) | Frequency (f) |
| fd |
0-10 | 5 | 7 | -20 | -140 |
10-20 | 15 | 8 | -10 | -80 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | + 10 | +100 |
40-50 | 45 | 5 | + 20 | +100 |
Total |
| 50 |
| -20 |
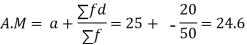
Q2) Find the value of median from the following data
Number of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
Number of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
S2) The given cumulative frequency distribution will first be converted into ordinary frequency as under:
Class interval | Cumulative frequency | Ordinary frequency |
0-5 | 29 | 29=29 |
5-10 | 224 | 224-29=105 |
10-15 | 465 | 465-224=241 |
15-20 | 582 | 582-465=117 |
20-25 | 634 | 634-582=52 |
25-30 | 644 | 644-634=10 |
30-35 | 650 | 650-644=6 |
35-40 | 653 | 653-650=3 |
40-45 | 655 | 655-653=2 |
Median = size of 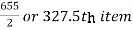
327.5th item lies in 10-15 which is the median class

Where l stands for lower limit of median class.
N stands for the total frequency
C stands for cumulative frequency just preceding the median class
i stands for class interval
f stands for frequency for the median class
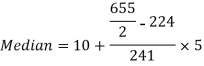
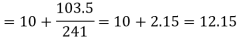
Q3) Find the mode from the following data
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
S3)
Age | Frequency | Cumulative frequency |
0-6 | 6 | 6 |
6-12 | 11 | 17 |
12-18 |
| 42 |
18-24 | 35 = f | 77 |
24-30 |
| 95 |
30-36 | 12 | 107 |
36-42 | 6 | 113 |
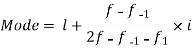
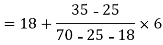
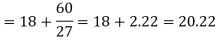
Q4) If coefficient of skewness is 0.64. Standard deviation is 13 and mean is 59.2, then find the mode and median.
S4)
We know that-
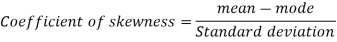
So that-
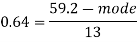
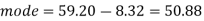
And we also know that-
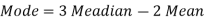
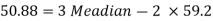
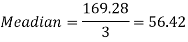
Q5) Calculate the Karl Pearson’s coefficient of skewness of marks obtained by 150 students.
|
S5) Mode is not well defined so that first we calculate mean and median-
Class | f | x | CF |
| fd |
|
0-10 | 10 | 5 | 10 | -3 | -30 | 90 |
10-20 | 40 | 15 | 50 | -2 | -80 | 160 |
20-30 | 20 | 25 | 70 | -1 | -20 | 20 |
30-40 | 0 | 35 | 70 | 0 | 0 | 0 |
40-50 | 10 | 45 | 80 | 1 | 10 | 10 |
50-60 | 40 | 55 | 120 | 2 | 80 | 160 |
60-70 | 16 | 65 | 136 | 3 | 48 | 144 |
70-80 | 14 | 75 | 150 | 4 | 56 | 244 |
Now,
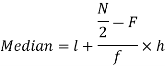

And
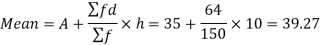
Standard deviation-
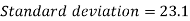
Then-

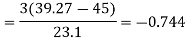
Q6) If on an average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
S6) Out of 10 ships one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 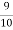
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)
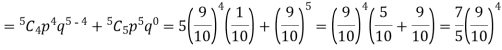
Q7) The probability that a man aged 60 will live to be 70 is 0.65. what is the probability that out of 10 men, now 60, at least seven will live to be 70?
S7) The probability that a man aged 60 will live to be 70
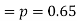

Number of men= n = 10 Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10) = P (7)+ P(8)+ P(9) + P(10) =
|
Q8) A die is tossed thrice. A success is getting 1 or 6 on a TOSS. Find the mean and variance of the number of successes.
S8) 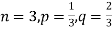
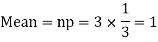
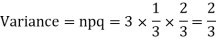
Q9) Assume that the probability of an individual coal miner being killed in a mine accident during a year is  . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
S9) 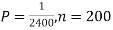

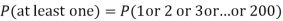
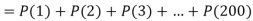
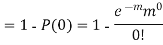
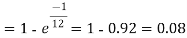
Q10) Find the area under the normal curve in each of the cases
(a) Z = 0 and z = 1.2
(b) Z = -0.68 and z = 0
(c) Z = -0.46 and z = -2.21
(d) Z = 0.81 and z = 1.94
(e) To the left of z = -0.6
(f) Right of z = -1.28
S10) (a) Area between Z = 0 and z = 1.2 =0.3849
(b)Area between z = 0 and z = -0.68 = 0.2518
(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\
= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)
=0.4865 + 0.1772 = 0.6637
(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)
= 0.4738-0.2910=0.1828
(e) Required area = 0.5-(Area between z = 0 and z = 0.6)
= 0.5-0.2257=0.2743
(f)Required area = (Area between z = 0 and z = -1.28)+0.5
= 0.3997+0.5
= 0.8997
Q11) In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
S11) Let 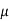 be the mean and
be the mean and 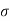 the S.D.
the S.D.
If x = 45, 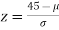
If x = 64, 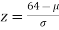
Area between 0 and 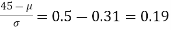
[From the table, for the area 0.19, z = 0.496)
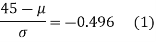
Area between z = 0 and z =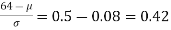
(from the table for area 0.42, z = 1.405)
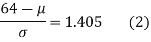
Solving (1) and (2) we get 
Q12) Psychological test of the intelligence and of Engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and Engineering ratio (E.R). Calculate the coefficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R. | 105 | 104 | 102 | 101 | 100 | 99 | 98 | 96 | 93 | 92 |
E.R. | 101 | 103 | 100 | 98 | 95 | 96 | 104 | 92 | 97 | 94 |
S12) We construct the following table
Student | Intelligence ratio x | Engineering ratio y y |
|
| XY |
A | 105 6 | 101 3 | 36 | 9 | 18 |
B | 104 5 | 103 5 | 25 | 25 | 25 |
C | 102 3 | 100 2 | 9 | 4 | 6 |
D | 101 2 | 98 0 | 4 | 0 | 0 |
E | 100 1 | 95 -3 | 1 | 9 | -3 |
F | 99 0 | 96 - 2 | 0 | 4 | 0 |
G | 98 -1 | 104 6 | 1 | 36 | -6 |
H | 96 -3 | 92 -6 | 9 | 36 | 18 |
I | 93 -6 | 97 -1 | 36 | 1 | 6 |
J | 92 -7 | 94 -4 | 49 | 16 | 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of x, i.e. 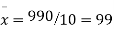 and mean of y, i.e.
and mean of y, i.e. 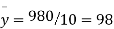
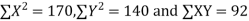
Substituting these value in the formula (1)p.744 we have
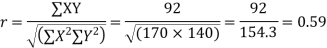
Q13) The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculate the coefficient of correlation between the age of the husband and that of the wife.
Age of husband | Age of wife | Total | ||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | |||
15-25 | 1 | 1 | - | - | - | - | 2 | |
25-35 | 2 | 12 | 1 | - | - | - | 15 | |
35-45 | - | 4 | 10 | 1 | - | - | 15 | |
45-55 | - | - | 3 | 6 | 1 | - | 10 | |
55-65 | - | - | - | 2 | 4 | 2 | 8 | |
65-75 | - | - | - | - | 1 | 2 | 3 | |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 | |
S13)
Age of husband | Age of wife x series | Suppose
| |||||||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
Total f | |||||||
Years | Midpoint x | 20 | 30 | 40 | 50 | 60 | 70 | ||||||
Age group | Midpoint y |
|
| -20 | -10 | 0 | 10 | 20 | 30 |
|
|
| |
| -2 | -1 | 0 | 1 | 2 | 3 | |||||||
15-25 | 20 | -20 | -2 | 4 1 | 2 1 |
|
|
|
| 2 | -4 | 8 | 6 |
25-35 | 30 | -10 | -1 | 4 2 | 12 12 | 0 1 |
|
|
| 15 | -15 | 15 | 16 |
35-45 | 40 | 0 | 0 |
| 0 4 | 0 10 | 0 1 |
|
| 15 | 0 | 0 | 0 |
45-55 | 50 |
|
|
|
| 0 3 | 6 6 | 2 1 |
| 10 | 10 | 10 | 8 |
55-65 | 60 |
|
|
|
|
| 4 2 | 16 4 | 12 2 | 8 | 16 | 32 | 32 |
65-75 | 70 |
|
|
|
|
|
| 6 1 | 18 2 | 3 | 9 | 27 | 24 |
Total f | 3 | 17 | 14 | 9 | 6 | 4 | 53 = n | 16 | 92 | 86 | |||
| -6 | -17 | 0 | 9 | 12 | 12 | 10 | Thick figures in small sqs. for Check:
From both sides | |||||
| 12 | 17 | 0 | 9 | 24 | 36 | 98 | ||||||
| 8 | 14 | 0 | 10 | 24 | 30 | 86 | ||||||
With the help of the above correlation table, we have
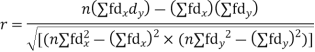
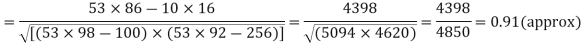
Q14) While calculating correlation coefficient between two variables x and y from 25 pairs of observations, the following results were obtained : n = 25,  Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
S14) To get the correct results, we subtract the incorrect values and add the corresponding correct values.
The correct results would be
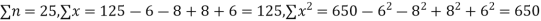
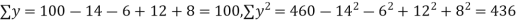
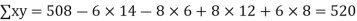
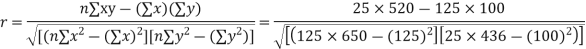
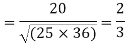
Q15) Three judges A,B,C give the following ranks. Find which pair of judges has common approach
A | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
B | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
C | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
S15) Here n = 10
A (=x) | Ranks by B(=y) | C (=z) |
x-y |
y - z |
z-x |
|
|
|
1 | 3 | 6 | -2 | -3 | 5 | 4 | 9 | 25 |
6 | 5 | 4 | 1 | 1 | -2 | 1 | 1 | 4 |
5 | 8 | 9 | -3 | -1 | 4 | 9 | 1 | 16 |
10 | 4 | 8 | 6 | -4 | -2 | 36 | 16 | 4 |
3 | 7 | 1 | -4 | 6 | -2 | 16 | 36 | 4 |
2 | 10 | 2 | -8 | 8 | 0 | 64 | 64 | 0 |
4 | 2 | 3 | 2 | -1 | -1 | 4 | 1 | 1 |
9 | 1 | 10 | 8 | -9 | 1 | 64 | 81 | 1 |
7 | 6 | 5 | 1 | 1 | -2 | 1 | 1 | 4 |
8 | 9 | 7 | -1 | 2 | -1 | 1 | 4 | 1 |
Total |
|
| 0 | 0 | 0 | 200 | 214 | 60 |

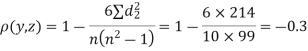
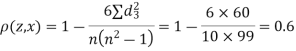
Since  is maximum, the pair of judge A and C have the nearest common approach.
is maximum, the pair of judge A and C have the nearest common approach.
Unit-4
Basic Statistics
Q1) Find the arithmetic mean for the following distribution
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
S1) Let assumed mean (a) = 25
Class | Mid-value (x) | Frequency (f) |
| fd |
0-10 | 5 | 7 | -20 | -140 |
10-20 | 15 | 8 | -10 | -80 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | + 10 | +100 |
40-50 | 45 | 5 | + 20 | +100 |
Total |
| 50 |
| -20 |
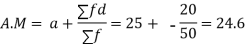
Q2) Find the value of median from the following data
Number of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
Number of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
S2) The given cumulative frequency distribution will first be converted into ordinary frequency as under:
Class interval | Cumulative frequency | Ordinary frequency |
0-5 | 29 | 29=29 |
5-10 | 224 | 224-29=105 |
10-15 | 465 | 465-224=241 |
15-20 | 582 | 582-465=117 |
20-25 | 634 | 634-582=52 |
25-30 | 644 | 644-634=10 |
30-35 | 650 | 650-644=6 |
35-40 | 653 | 653-650=3 |
40-45 | 655 | 655-653=2 |
Median = size of 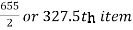
327.5th item lies in 10-15 which is the median class

Where l stands for lower limit of median class.
N stands for the total frequency
C stands for cumulative frequency just preceding the median class
i stands for class interval
f stands for frequency for the median class
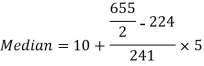
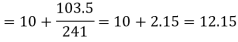
Q3) Find the mode from the following data
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
S3)
Age | Frequency | Cumulative frequency |
0-6 | 6 | 6 |
6-12 | 11 | 17 |
12-18 |
| 42 |
18-24 | 35 = f | 77 |
24-30 |
| 95 |
30-36 | 12 | 107 |
36-42 | 6 | 113 |
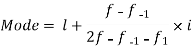
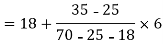
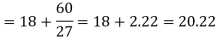
Q4) If coefficient of skewness is 0.64. Standard deviation is 13 and mean is 59.2, then find the mode and median.
S4)
We know that-
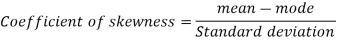
So that-
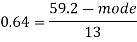
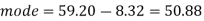
And we also know that-

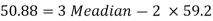
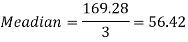
Q5) Calculate the Karl Pearson’s coefficient of skewness of marks obtained by 150 students.
|
S5) Mode is not well defined so that first we calculate mean and median-
Class | f | x | CF |
| fd |
|
0-10 | 10 | 5 | 10 | -3 | -30 | 90 |
10-20 | 40 | 15 | 50 | -2 | -80 | 160 |
20-30 | 20 | 25 | 70 | -1 | -20 | 20 |
30-40 | 0 | 35 | 70 | 0 | 0 | 0 |
40-50 | 10 | 45 | 80 | 1 | 10 | 10 |
50-60 | 40 | 55 | 120 | 2 | 80 | 160 |
60-70 | 16 | 65 | 136 | 3 | 48 | 144 |
70-80 | 14 | 75 | 150 | 4 | 56 | 244 |
Now,
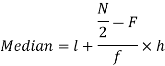
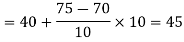
And
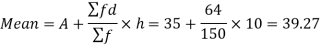
Standard deviation-
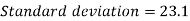
Then-
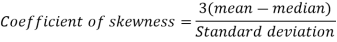
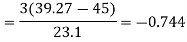
Q6) If on an average one ship in every ten is wrecked. Find the probability that out of 5 ships expected to arrive, 4 at least we will arrive safely.
S6) Out of 10 ships one ship is wrecked.
I.e. nine ships out of 10 ships are safe, P (safety) = 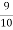
P (at least 4 ships out of 5 are safe) = P (4 or 5) = P (4) + P(5)

Q7) The probability that a man aged 60 will live to be 70 is 0.65. what is the probability that out of 10 men, now 60, at least seven will live to be 70?
S7) The probability that a man aged 60 will live to be 70
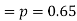
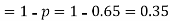
Number of men= n = 10 Probability that at least 7 men will live to 70 = (7 or 8 or 9 or 10) = P (7)+ P(8)+ P(9) + P(10) =
|
Q8) A die is tossed thrice. A success is getting 1 or 6 on a TOSS. Find the mean and variance of the number of successes.
S8) 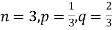
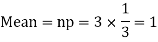
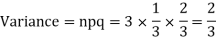
Q9) Assume that the probability of an individual coal miner being killed in a mine accident during a year is  . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
S9) 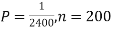
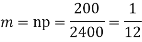
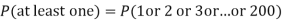
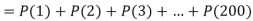
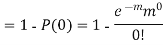
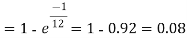
Q10) Find the area under the normal curve in each of the cases
(a) Z = 0 and z = 1.2
(b) Z = -0.68 and z = 0
(c) Z = -0.46 and z = -2.21
(d) Z = 0.81 and z = 1.94
(e) To the left of z = -0.6
(f) Right of z = -1.28
S10) (a) Area between Z = 0 and z = 1.2 =0.3849
(b)Area between z = 0 and z = -0.68 = 0.2518
(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\
= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)
=0.4865 + 0.1772 = 0.6637
(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)
= 0.4738-0.2910=0.1828
(e) Required area = 0.5-(Area between z = 0 and z = 0.6)
= 0.5-0.2257=0.2743
(f)Required area = (Area between z = 0 and z = -1.28)+0.5
= 0.3997+0.5
= 0.8997
Q11) In a normal distribution, 31% of the items are 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
S11) Let  be the mean and
be the mean and  the S.D.
the S.D.
If x = 45, 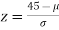
If x = 64, 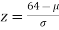
Area between 0 and 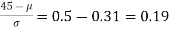
[From the table, for the area 0.19, z = 0.496)

Area between z = 0 and z =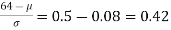
(from the table for area 0.42, z = 1.405)
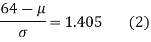
Solving (1) and (2) we get 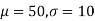
Q12) Psychological test of the intelligence and of Engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and Engineering ratio (E.R). Calculate the coefficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R. | 105 | 104 | 102 | 101 | 100 | 99 | 98 | 96 | 93 | 92 |
E.R. | 101 | 103 | 100 | 98 | 95 | 96 | 104 | 92 | 97 | 94 |
S12) We construct the following table
Student | Intelligence ratio x | Engineering ratio y y |
|
| XY |
A | 105 6 | 101 3 | 36 | 9 | 18 |
B | 104 5 | 103 5 | 25 | 25 | 25 |
C | 102 3 | 100 2 | 9 | 4 | 6 |
D | 101 2 | 98 0 | 4 | 0 | 0 |
E | 100 1 | 95 -3 | 1 | 9 | -3 |
F | 99 0 | 96 - 2 | 0 | 4 | 0 |
G | 98 -1 | 104 6 | 1 | 36 | -6 |
H | 96 -3 | 92 -6 | 9 | 36 | 18 |
I | 93 -6 | 97 -1 | 36 | 1 | 6 |
J | 92 -7 | 94 -4 | 49 | 16 | 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of x, i.e. 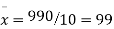 and mean of y, i.e.
and mean of y, i.e. 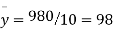
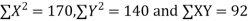
Substituting these value in the formula (1)p.744 we have
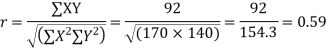
Q13) The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculate the coefficient of correlation between the age of the husband and that of the wife.
Age of husband | Age of wife | Total | ||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | |||
15-25 | 1 | 1 | - | - | - | - | 2 | |
25-35 | 2 | 12 | 1 | - | - | - | 15 | |
35-45 | - | 4 | 10 | 1 | - | - | 15 | |
45-55 | - | - | 3 | 6 | 1 | - | 10 | |
55-65 | - | - | - | 2 | 4 | 2 | 8 | |
65-75 | - | - | - | - | 1 | 2 | 3 | |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 | |
S13)
Age of husband | Age of wife x series | Suppose
| |||||||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
Total f | |||||||
Years | Midpoint x | 20 | 30 | 40 | 50 | 60 | 70 | ||||||
Age group | Midpoint y |
|
| -20 | -10 | 0 | 10 | 20 | 30 |
|
|
| |
| -2 | -1 | 0 | 1 | 2 | 3 | |||||||
15-25 | 20 | -20 | -2 | 4 1 | 2 1 |
|
|
|
| 2 | -4 | 8 | 6 |
25-35 | 30 | -10 | -1 | 4 2 | 12 12 | 0 1 |
|
|
| 15 | -15 | 15 | 16 |
35-45 | 40 | 0 | 0 |
| 0 4 | 0 10 | 0 1 |
|
| 15 | 0 | 0 | 0 |
45-55 | 50 |
|
|
|
| 0 3 | 6 6 | 2 1 |
| 10 | 10 | 10 | 8 |
55-65 | 60 |
|
|
|
|
| 4 2 | 16 4 | 12 2 | 8 | 16 | 32 | 32 |
65-75 | 70 |
|
|
|
|
|
| 6 1 | 18 2 | 3 | 9 | 27 | 24 |
Total f | 3 | 17 | 14 | 9 | 6 | 4 | 53 = n | 16 | 92 | 86 | |||
| -6 | -17 | 0 | 9 | 12 | 12 | 10 | Thick figures in small sqs. for Check:
From both sides | |||||
| 12 | 17 | 0 | 9 | 24 | 36 | 98 | ||||||
| 8 | 14 | 0 | 10 | 24 | 30 | 86 | ||||||
With the help of the above correlation table, we have


Q14) While calculating correlation coefficient between two variables x and y from 25 pairs of observations, the following results were obtained : n = 25,  Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
S14) To get the correct results, we subtract the incorrect values and add the corresponding correct values.
The correct results would be

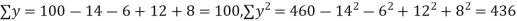
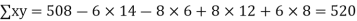
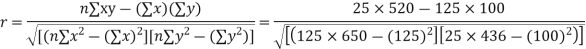
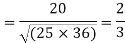
Q15) Three judges A,B,C give the following ranks. Find which pair of judges has common approach
A | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
B | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
C | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
S15) Here n = 10
A (=x) | Ranks by B(=y) | C (=z) |
x-y |
y - z |
z-x |
|
|
|
1 | 3 | 6 | -2 | -3 | 5 | 4 | 9 | 25 |
6 | 5 | 4 | 1 | 1 | -2 | 1 | 1 | 4 |
5 | 8 | 9 | -3 | -1 | 4 | 9 | 1 | 16 |
10 | 4 | 8 | 6 | -4 | -2 | 36 | 16 | 4 |
3 | 7 | 1 | -4 | 6 | -2 | 16 | 36 | 4 |
2 | 10 | 2 | -8 | 8 | 0 | 64 | 64 | 0 |
4 | 2 | 3 | 2 | -1 | -1 | 4 | 1 | 1 |
9 | 1 | 10 | 8 | -9 | 1 | 64 | 81 | 1 |
7 | 6 | 5 | 1 | 1 | -2 | 1 | 1 | 4 |
8 | 9 | 7 | -1 | 2 | -1 | 1 | 4 | 1 |
Total |
|
| 0 | 0 | 0 | 200 | 214 | 60 |
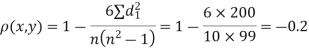
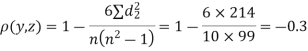
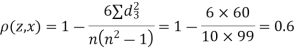
Since 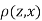 is maximum, the pair of judge A and C have the nearest common approach.
is maximum, the pair of judge A and C have the nearest common approach.