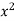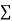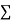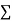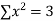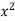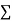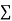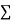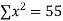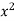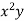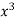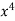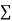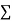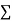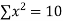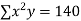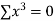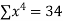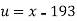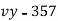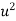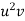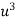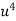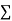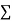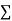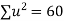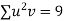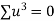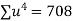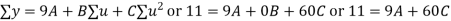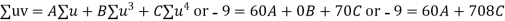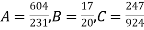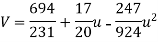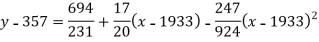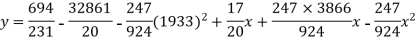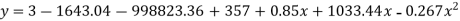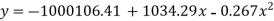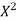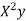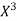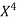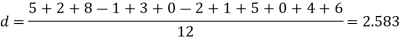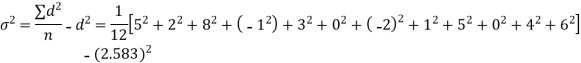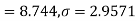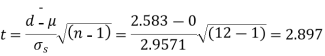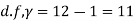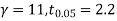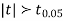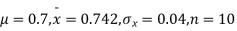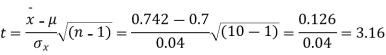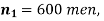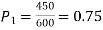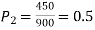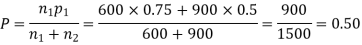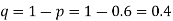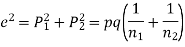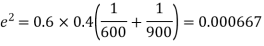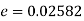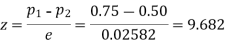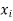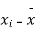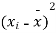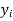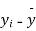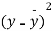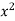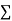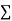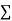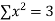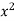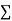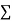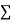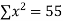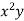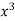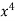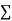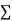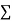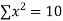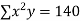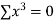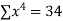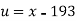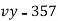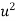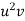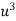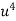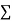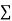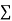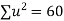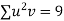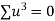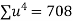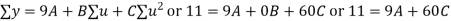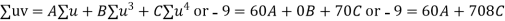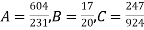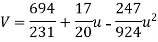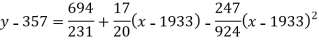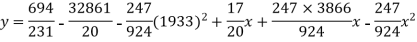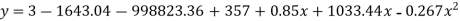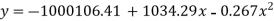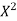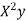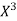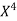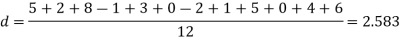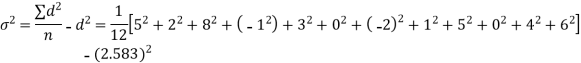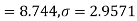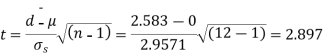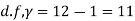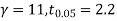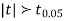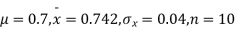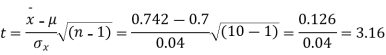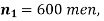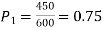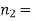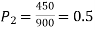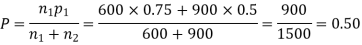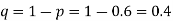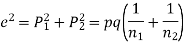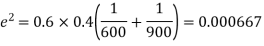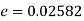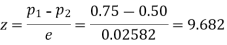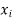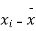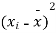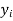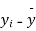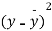Unit-5
Applied Statistics
Q1) Find the best values of a and b so that y = a + bx fits the data given in the table
x | 0 | 1 | 2 | 3 | 4 |
y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
S1)
y = a + bx
x | y | xy |
|
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
|
|
|
|
Normal equations, 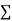 y= na+ b
y= na+ b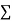 x (2)
x (2)
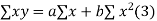
On putting the values of 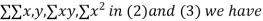
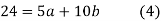
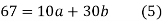
On solving (4) and (5) we get,
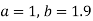
On substituting the values of a and b in (1) we get
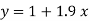
Q2) By the method of least squares, find the straight line that best fits the following data :
x | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
S2) Let the equation of the straight line best fit be y = a + bx. (1)
x | y | x y |
|
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
|
|
|
|
Normal equations are 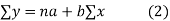
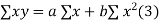
On putting the values of 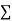 x,
x, 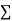 y,
y, 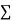 xy and
xy and 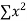 in (2) and (3) we have
in (2) and (3) we have
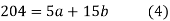
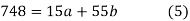
On solving equations (4) and (5) we get
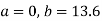
On substituting the values of (a) and (b) in (1) we get,
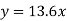
Q3) Find the least squares approximation of second degree for the discrete data
x | 2 | -1 | 0 | 1 | 2 |
y | 15 | 1 | 1 | 3 | 19 |
S3) Let the equation of second degree polynomial be 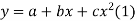
x | y | xy |
|
|
|
|
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
|
|
|
|
|
|
|
Normal equations are 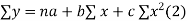
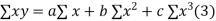
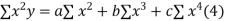
On putting the values of 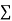 x,
x, 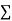 y,
y,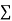 xy,
xy, 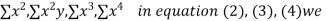 have
have
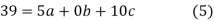
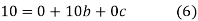
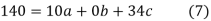
On solving (5),(6),(7), we get, 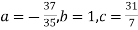
The required polynomial of second degree is
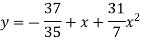
Q4) Fit a second degree parabola to the following data by least square method:
x | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
y | 352 | 356 | 357 | 358 | 360 | 361 | 365 | 360 | 359 |
S4) Taking 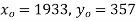
Taking 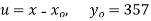
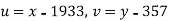
The equation 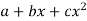 is transformed to
is transformed to 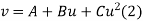
x |
| y |
| uv |
|
|
|
|
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 350 | 2 | 8 | 16 | 32 | 64 | 256 |
Total |
|
|
|
|
|
|
|
|
Normal equations are
On solving these equations we get
|
Q5) Fit a second degree parabola to the following data.
x=1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
y=1.1 | 1.3 | 1.6 | 2.0 | 2.7 | 3.4 | 4.1 |
S5)
We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.
Let the parabola of fit be y = a + bX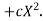 The values of
The values of 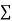 X etc. Are calculated as below:
X etc. Are calculated as below:
x | X | y | Xy |
|
|
|
|
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -5 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2.0 | 0.0 | 0 | 0.0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.3 | 28 | 69.9 | 0 | 196 |
The normal equations are
7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9
Solving these as simultaneous equations we get
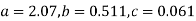
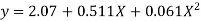
Replacing X bye 2x – 5 in the above equation we get
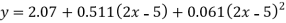
Which simplifies to y =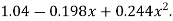 This is the required parabola of the best fit
This is the required parabola of the best fit
Q6) A certain stimulus administered to each of 12 patients resulted in the following increases off blood pressure: 5, 2, 8, -1, 3, 0, -2, 1, 5, 0, 4, 6. Can it be concluded that the stimulus will in general be accompanied by an increase in blood pressure.
S6) Let us assume that the stimulus administered to all the 12 patients will increases the blood pressure. Taking the population to be normal with mean μ = 0 and S.D. 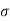
Here For Since the |
Q7) A mechanism is making engine parts with axle diameter of 0.7 inch. A random sample of 10 parts shows mean diameter 0.742 inches with a standard deviation of 0.04 inch. On the basis of this sample would you say that the work is inferior?
S7) Here we have,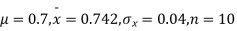
Taking the hypothesis that the product is not inferior that is there is no significant difference between 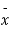 and μ.
and μ.
|
Degree of freedom 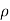 = 10-1=9
= 10-1=9
For 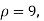 we get from table IV,
we get from table IV, 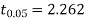
As the calculated value of 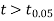 the value of t is significant at 5% level of significance. This implies that
the value of t is significant at 5% level of significance. This implies that 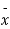 differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. In fact, the work is inferior even at 2% level of significance.
differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. In fact, the work is inferior even at 2% level of significance.
Q8) In two large populations there are 30% and 25% respectively of fair haired people. Is this difference likely to be hidden in samples of 1200 and 900 respectively from the two populations?
S8) Here 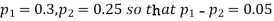
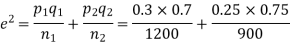
So that, 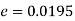
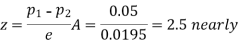
Hence it is unlikely that the real difference will be hidden.
Q9) In a sample of 600 men from a certain City 450 are found smokers. In another sample of 900 men from another City, 450 are smokers. do the data indicate that the cities are significantly different with respect to the habit of smoking among men?
S9)
z>3 so that the difference is significant.
|
Q10) From a random sample of 10 pigs fed on diet A. The increase in weight in a certain period were 10, 6, 16, 17, 13, 12, 8, 14, 15, 9 lbs. For another random sample of 12 pig’s fat on diet B, the increases in the same period were 7, 13, 22, 15, 12, 14, 18, 8, 21, 23, 10, 17 lbs. Test whether diets A and B differ significantly as regards their effects on increases in weight?
S10) We calculate the means and standard deviation of the samples as follows
| Diet A |
|
| Diet B |
|
|
|
|
|
|
|
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 18 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 23 | 2 | 4 |
120 | 0 | 120 | 10 | 0 | 314 |
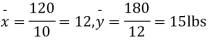
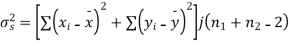
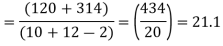
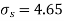
Assuming that the samples do not differ in weight so far as two diets are concerned i.e. 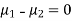
Hence, 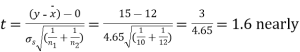
Here, 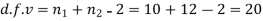
For 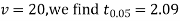
The calculated value of 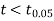
Hence the difference between the sample means is not significant that is the two diets do not differ significantly as regards their effects on increase in weight.
Unit-5
Applied Statistics
Q1) Find the best values of a and b so that y = a + bx fits the data given in the table
x | 0 | 1 | 2 | 3 | 4 |
y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
S1)
y = a + bx
x | y | xy |
|
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
|
|
|
|
Normal equations, 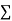 y= na+ b
y= na+ b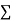 x (2)
x (2)
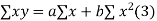
On putting the values of 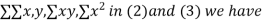
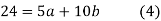
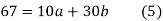
On solving (4) and (5) we get,
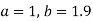
On substituting the values of a and b in (1) we get
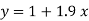
Q2) By the method of least squares, find the straight line that best fits the following data :
x | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
S2) Let the equation of the straight line best fit be y = a + bx. (1)
x | y | x y |
|
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
|
|
|
|
Normal equations are 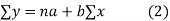
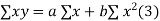
On putting the values of 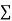 x,
x, 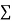 y,
y, 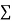 xy and
xy and 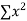 in (2) and (3) we have
in (2) and (3) we have
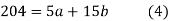
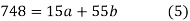
On solving equations (4) and (5) we get
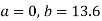
On substituting the values of (a) and (b) in (1) we get,
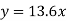
Q3) Find the least squares approximation of second degree for the discrete data
x | 2 | -1 | 0 | 1 | 2 |
y | 15 | 1 | 1 | 3 | 19 |
S3) Let the equation of second degree polynomial be 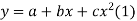
x | y | xy |
|
|
|
|
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
|
|
|
|
|
|
|
Normal equations are 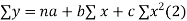
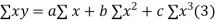
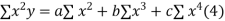
On putting the values of 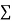 x,
x, 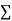 y,
y,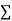 xy,
xy, 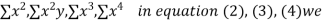 have
have
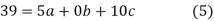
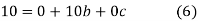
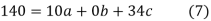
On solving (5),(6),(7), we get, 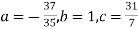
The required polynomial of second degree is
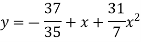
Q4) Fit a second degree parabola to the following data by least square method:
x | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
y | 352 | 356 | 357 | 358 | 360 | 361 | 365 | 360 | 359 |
S4) Taking 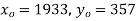
Taking 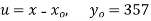
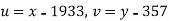
The equation 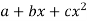 is transformed to
is transformed to 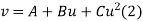
x |
| y |
| uv |
|
|
|
|
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 350 | 2 | 8 | 16 | 32 | 64 | 256 |
Total |
|
|
|
|
|
|
|
|
Normal equations are
On solving these equations we get
|
Q5) Fit a second degree parabola to the following data.
x=1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
y=1.1 | 1.3 | 1.6 | 2.0 | 2.7 | 3.4 | 4.1 |
S5)
We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.
Let the parabola of fit be y = a + bX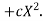 The values of
The values of 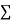 X etc. Are calculated as below:
X etc. Are calculated as below:
x | X | y | Xy |
|
|
|
|
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -5 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2.0 | 0.0 | 0 | 0.0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.3 | 28 | 69.9 | 0 | 196 |
The normal equations are
7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9
Solving these as simultaneous equations we get
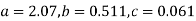
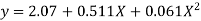
Replacing X bye 2x – 5 in the above equation we get
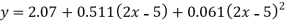
Which simplifies to y =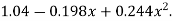 This is the required parabola of the best fit
This is the required parabola of the best fit
Q6) A certain stimulus administered to each of 12 patients resulted in the following increases off blood pressure: 5, 2, 8, -1, 3, 0, -2, 1, 5, 0, 4, 6. Can it be concluded that the stimulus will in general be accompanied by an increase in blood pressure.
S6) Let us assume that the stimulus administered to all the 12 patients will increases the blood pressure. Taking the population to be normal with mean μ = 0 and S.D. 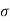
Here For Since the |
Q7) A mechanism is making engine parts with axle diameter of 0.7 inch. A random sample of 10 parts shows mean diameter 0.742 inches with a standard deviation of 0.04 inch. On the basis of this sample would you say that the work is inferior?
S7) Here we have,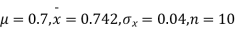
Taking the hypothesis that the product is not inferior that is there is no significant difference between 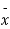 and μ.
and μ.
|
Degree of freedom 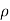 = 10-1=9
= 10-1=9
For 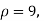 we get from table IV,
we get from table IV, 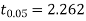
As the calculated value of 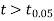 the value of t is significant at 5% level of significance. This implies that
the value of t is significant at 5% level of significance. This implies that 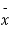 differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. In fact, the work is inferior even at 2% level of significance.
differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. In fact, the work is inferior even at 2% level of significance.
Q8) In two large populations there are 30% and 25% respectively of fair haired people. Is this difference likely to be hidden in samples of 1200 and 900 respectively from the two populations?
S8) Here 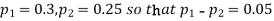
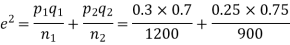
So that, 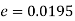
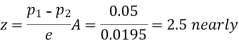
Hence it is unlikely that the real difference will be hidden.
Q9) In a sample of 600 men from a certain City 450 are found smokers. In another sample of 900 men from another City, 450 are smokers. do the data indicate that the cities are significantly different with respect to the habit of smoking among men?
S9)
z>3 so that the difference is significant.
|
Q10) From a random sample of 10 pigs fed on diet A. The increase in weight in a certain period were 10, 6, 16, 17, 13, 12, 8, 14, 15, 9 lbs. For another random sample of 12 pig’s fat on diet B, the increases in the same period were 7, 13, 22, 15, 12, 14, 18, 8, 21, 23, 10, 17 lbs. Test whether diets A and B differ significantly as regards their effects on increases in weight?
S10) We calculate the means and standard deviation of the samples as follows
| Diet A |
|
| Diet B |
|
|
|
|
|
|
|
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 18 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 23 | 2 | 4 |
120 | 0 | 120 | 10 | 0 | 314 |
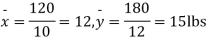
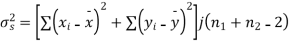
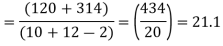
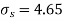
Assuming that the samples do not differ in weight so far as two diets are concerned i.e. 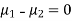
Hence, 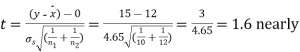
Here, 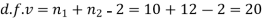
For 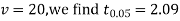
The calculated value of 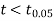
Hence the difference between the sample means is not significant that is the two diets do not differ significantly as regards their effects on increase in weight.