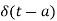SS
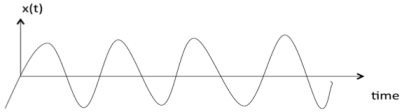
Unit-1 Introduction to Signals and Systems Q1)Explain Periodicity?A1) The signal’s behaviour/graph repeats after every T. Therefore, x(t) = x(t + nT) or x(t) = x(t – nT) where, T is the fundamental period. So we can say that the signal remains unchanged when shifted by multiples of T.Q2)Differentiate between deterministic and non determinstic signal?A2)DeterministicA signal is said to be deterministic if there is no uncertainty with respect to its value at any instant of time or the signals which can be defined exactly by a mathematical formula are known as deterministic signals.
Deterministic signalRandomA signal is said to be non-deterministic(stochastic) if there is uncertainty with respect to its value at some instant of time. Non-deterministic signals are random in nature hence they are called random signals. Random signals cannot be described by a mathematical equation. They are modelled in probabilistic terms.
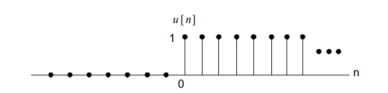
Random signal Q3) Explain unit step sequence and unit impulse sequence?A3) Unit step sequence:The unit step sequence is defined as:u(n) = 1 for n 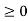 =0 for n<0
=0 for n<0
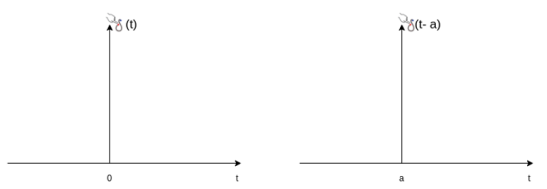
Figure . Unit Step SignalUnit Impulse The impulse function occupies an important place in signal analysis. It is defined as 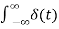 dt =1 and δ(t) =0 for t
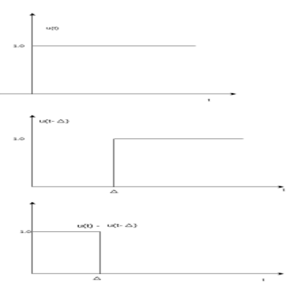
dt =1 and δ(t) =0 for t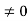 The impulse function has zero amplitude everywhere except at t=0. At t=0 the amplitude is infinity such that the area under the curve is equal to one. The unit impulse function can be obtained by using limiting process on the rectangular pulse as shown in figure. Note that the area under the rectangular pulse is equal to unity.
The impulse function has zero amplitude everywhere except at t=0. At t=0 the amplitude is infinity such that the area under the curve is equal to one. The unit impulse function can be obtained by using limiting process on the rectangular pulse as shown in figure. Note that the area under the rectangular pulse is equal to unity.
Impulse functionThe rectangular pulse function of the figure can be expressed as x(t) = 1/ ∆ [ u(t) – u(t-∆)] …………………………………..(1)The impulse function can be obtained when the width ∆ ->0 that is δ(t) = lim ∆-> 0 x(t)= lim ∆-> 0 1/ ∆ [ u(t) – u(t-∆)]
The delayed unit impulse function is defined as
Q4) Explain Continuous and Discrete time signal?A4) A continuous time system is one which operates on the continuous time input signal and produces a continuous-time output signal.

 x(t) y(t) Figure . I/O of continuous time signalIf the input is x(t) and output is y(t) then y(t) = T{x(t)}That is x(t ) is transformed to y(t).Example : Amplifiers, filters, motors etc Discrete time system is one which operates on discrete time input signal and produces a discrete-time output signal.
x(t) y(t) Figure . I/O of continuous time signalIf the input is x(t) and output is y(t) then y(t) = T{x(t)}That is x(t ) is transformed to y(t).Example : Amplifiers, filters, motors etc Discrete time system is one which operates on discrete time input signal and produces a discrete-time output signal.

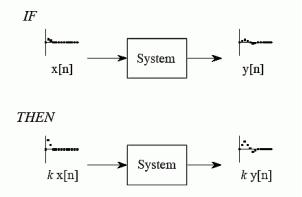
 x(n) y(n) Figure . I/O of Discrete time signal If the input is x(n) and output y(n) then y(n) = T[x(n)] Q5) Explain Linearity property?A5) Constitutes two properties:Additivity/ Super position If x1(t) -> y1(t)and x2(t) -> y2(t)then x1(t) + x2(t) -> y1(t) + y2(t)Property of scalingif x1(t) -> y1(t)a * x1(t) -> a * y1(t)If both are satisfied, then system is lineary(t) = x2(t)The responses due to inputs x1(t) and x2(t) are given by y1(t) = x1 2(t)y2(t) = x2 2(t) The output due to weighted sum of inputs is y3(t) = T[ax1(t) + bx2(t)] = [ax1(t) + bx2(t)]2The weighted sum of inputs a y1(t) + by2(t) = ax12(t) + b x2 2(t)y3(t) ≠ ay1(t) + by2(t)System is non-linear. Q6) Explain additive and homogeneity property?A6) HomogeneityHomogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.That is a change in x[n] will result in a change in y [n]Also, a change in k x[n] will result in a change in k y[n]
x(n) y(n) Figure . I/O of Discrete time signal If the input is x(n) and output y(n) then y(n) = T[x(n)] Q5) Explain Linearity property?A5) Constitutes two properties:Additivity/ Super position If x1(t) -> y1(t)and x2(t) -> y2(t)then x1(t) + x2(t) -> y1(t) + y2(t)Property of scalingif x1(t) -> y1(t)a * x1(t) -> a * y1(t)If both are satisfied, then system is lineary(t) = x2(t)The responses due to inputs x1(t) and x2(t) are given by y1(t) = x1 2(t)y2(t) = x2 2(t) The output due to weighted sum of inputs is y3(t) = T[ax1(t) + bx2(t)] = [ax1(t) + bx2(t)]2The weighted sum of inputs a y1(t) + by2(t) = ax12(t) + b x2 2(t)y3(t) ≠ ay1(t) + by2(t)System is non-linear. Q6) Explain additive and homogeneity property?A6) HomogeneityHomogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.That is a change in x[n] will result in a change in y [n]Also, a change in k x[n] will result in a change in k y[n]
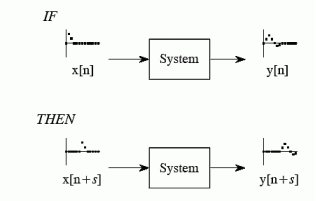
Figure. HomogenityAdditivityConsider a system where input x1[n] produces an output y1[n]. Similarly x2[n] produces y2[n]. The system is additive when x1[n] + x2[n] = y1[n] + y2[n]In other words signals added at the input will produce signals added at the output. Q7) Explain Shift invariance property?A7) Shift invariance means that a shift in the input signal will result in an identical shift in the output signal If x[n] -> y[n]Then x[n+s] -> y[n +s] for any constant s
Figure. Shift Invariance Q8) Explain causality property?A8) The property of causality is a requirement for a system to be realizable in reality. Causality means that the output of the system does not depend on future inputs, but only on past input.Examples of casual system:y(t) = x(t) + x(t-1)y(n) = n x(n) + x(n-3) Examples of non-casual systemy(t) = x(t+3) + x 2 (t)y(n) = x(2n) For example y(t) = 2 x(t) + 3 x(t-3) let t=1 therefore y (1) = 2 x(1) + 3 x(-2)The system output only depends upon present and past inputs. Hence, the system is causal.y(t) = 2 x(t) + 3 x(t – 3) + 6 x( t+3)let t=1 the system output is y(1) = 2x(1) + 3 x(-2) + 6 x( 4)Here the output depends future input. Hence non –casual.Q9) Explain the property of stability?A9) Figure Stability of the system An input signal x(t) is said to be bounded if it satisfies the condition |x(t) |≤Mx < ∞ for all t.Similarly, the output signal is bounded if it satisfies the condition |y(t)| ≤My < ∞ The example for bounded and unbounded signals is as shown in the figure.Note: For a bounded signal, the amplitude is finite.Example 1: y (t) = x2(t)Let the input is u(t) that is unit step then output y(t) = u2(t) = u(t) = bounded output.Hence, the system is stable.Example 2: y (t) = ∫x(t)dt∫x(t)dtLet the input be u (t) then output y(t) = ∫u(t)dt but ∫ u(t)dt = ramp signal It is unbounded because the amplitude of ramp is not finite and tends to become infinite when t →infiniteHence, the system is unstable. Q10) Explain Realizability?A10) Consider the first system, y(t)=x(t−1)y(t)=x(t−1) is a causal system, because its output is a time-delayed version of the original signal.On the other hand, the second system y(t)=x(t+1)y(t)=x(t+1), is non-causal. This system returns a time-advanced version of the input signal. This means, that for example at the output time t=0, the system requires access to the value of the input signal at time t=1. Clearly, this is impossible in a realizable system, as nobody can predict the future.
|
|
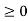 =0 for n<0
=0 for n<0
|
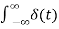 dt =1 and δ(t) =0 for t
dt =1 and δ(t) =0 for t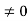 The impulse function has zero amplitude everywhere except at t=0. At t=0 the amplitude is infinity such that the area under the curve is equal to one. The unit impulse function can be obtained by using limiting process on the rectangular pulse as shown in figure. Note that the area under the rectangular pulse is equal to unity.
The impulse function has zero amplitude everywhere except at t=0. At t=0 the amplitude is infinity such that the area under the curve is equal to one. The unit impulse function can be obtained by using limiting process on the rectangular pulse as shown in figure. Note that the area under the rectangular pulse is equal to unity.
|
Unit impulse with delay function
|
and Impulse function
|


 x(t) y(t) Figure . I/O of continuous time signalIf the input is x(t) and output is y(t) then y(t) = T{x(t)}That is x(t ) is transformed to y(t).Example : Amplifiers, filters, motors etc Discrete time system is one which operates on discrete time input signal and produces a discrete-time output signal.
x(t) y(t) Figure . I/O of continuous time signalIf the input is x(t) and output is y(t) then y(t) = T{x(t)}That is x(t ) is transformed to y(t).Example : Amplifiers, filters, motors etc Discrete time system is one which operates on discrete time input signal and produces a discrete-time output signal.

 x(n) y(n) Figure . I/O of Discrete time signal If the input is x(n) and output y(n) then y(n) = T[x(n)] Q5) Explain Linearity property?A5) Constitutes two properties:Additivity/ Super position If x1(t) -> y1(t)and x2(t) -> y2(t)then x1(t) + x2(t) -> y1(t) + y2(t)Property of scalingif x1(t) -> y1(t)a * x1(t) -> a * y1(t)If both are satisfied, then system is lineary(t) = x2(t)The responses due to inputs x1(t) and x2(t) are given by y1(t) = x1 2(t)y2(t) = x2 2(t) The output due to weighted sum of inputs is y3(t) = T[ax1(t) + bx2(t)] = [ax1(t) + bx2(t)]2The weighted sum of inputs a y1(t) + by2(t) = ax12(t) + b x2 2(t)y3(t) ≠ ay1(t) + by2(t)System is non-linear. Q6) Explain additive and homogeneity property?A6) HomogeneityHomogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.That is a change in x[n] will result in a change in y [n]Also, a change in k x[n] will result in a change in k y[n]
x(n) y(n) Figure . I/O of Discrete time signal If the input is x(n) and output y(n) then y(n) = T[x(n)] Q5) Explain Linearity property?A5) Constitutes two properties:Additivity/ Super position If x1(t) -> y1(t)and x2(t) -> y2(t)then x1(t) + x2(t) -> y1(t) + y2(t)Property of scalingif x1(t) -> y1(t)a * x1(t) -> a * y1(t)If both are satisfied, then system is lineary(t) = x2(t)The responses due to inputs x1(t) and x2(t) are given by y1(t) = x1 2(t)y2(t) = x2 2(t) The output due to weighted sum of inputs is y3(t) = T[ax1(t) + bx2(t)] = [ax1(t) + bx2(t)]2The weighted sum of inputs a y1(t) + by2(t) = ax12(t) + b x2 2(t)y3(t) ≠ ay1(t) + by2(t)System is non-linear. Q6) Explain additive and homogeneity property?A6) HomogeneityHomogeneity means change in input signals amplitude results in a corresponding change in the output signal’s amplitude.That is a change in x[n] will result in a change in y [n]Also, a change in k x[n] will result in a change in k y[n]
|
|
0 matching results found