Unit - 1
Discrete-time signals and systems
Q1) Consider the following signal set:
Find the convolution of above?
A1)
By inspection, the signals can be expressed in terms of the following two basis functions:
Note that the basis is orthogonal
Also note that each these functions have unit energy
We say that they form an orthonormal basis.
Q2) Find the homogenous solution for the difference equation y[n]-
y[n-1]+
y[n-2]=1+3-n. Given y[-2] = 0 and y[-1]=2
A2)
For homogeneous solution
Y[n] = rn
rn-
rn-1+
rn-2 = 0
rn-2(r2-
r+
) = 0
Solving above equation we get
r= 
and r=1
Roots are distinct so the solution will be of the form
y[n] = p1
+ p2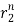
y[n] = p12-n +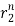
Particular Solution:
Input signal x[n] | Particular solution yp[n] |
1) A constant | k |
(2) A Mn | KMn |
(3) AnM | k0nM+k1nM-1+ . . . + kM |
(4) AnnM | An(k0nM + k1 nM-1 + . . . + kM) |
(5)  | k1 cos ω0n + k sin ω0n |
The complete solution of any difference equation is the sum of homogeneous solution and the particular solution.
Q3) For the difference equation find the particular solution x[n] = 3n and y[n] = x[n]+
y[n-1]- 
y[n-2]?
A3)
As x[n] = 3n
From table the particular solution will be y[n] = k3n
y[n] = x[n]+
y[n-1]-
y[n-2]
k3nu(n) = 3nu(n)+
k 3n-1u(n-1)-
k3n-2u(n-2)
Finding k for n≥2
K 32 = 32+
k 32-1-
k 32-2
9k-
k+
k = 9
k= 27/20
y[n]= 
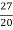3n
Q4) The continuous-time signal x(t) = cos(200πt) is used as the input for a CD converter with the sampling period 1/300 sec. Determine the resultant discrete-time signal x[n].
A4)
We know,
X[n] =x(nT)
= cos(200πnT)
= cos(2πn/3) , where n= -1,0,1,2……
The frequency in x(t) is 200π rad/s while that of x[n] is 2π/3.
Q5) Determine the Nyquist frequency and Nyquist rate for the continuous-time signal x(t) which has the form of X(t) = 1+ sin(2000πt) + cos (4000πt)
A5)
The frequencies are 0, 2000π and 4000π.
The Nyquist frequency is 4000π rad/s and the Nyquist rate is 8000π rad/s.
Q6) Consider an analog signal 
A6)
The frequency in the analog signal
The largest frequency is
The Nyquist rate is
Q7) The analog signal 
- What is the Nyquist rate for this signal?
- Using a sampling rate
. What is discrete time signal obtained after sampling? - What is analog signal
we can reconstruct from the sample if we use ideal interpolation?
A7)
- The frequency of the analog signal are
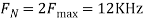
- For
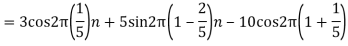
For 
,the folding frequency is 
Hence 
is not effected by aliasing
Is changed by the aliasing effect 
Is changed by the aliasing effect 
So that normalizing frequencies are
The analog signal that we can recover is
Q8) For given signal
- Find the minimum sampling rate required to avoid aliasing.
- If
, what is the discrete time signal after sampling? - If
, what is the discrete time signal after sampling? - What is the frequency F of a sinusoidal that yields sampling identical to obtained in part c?
A8)
a.
The minimum sampling rate is
And the discrete time signal is
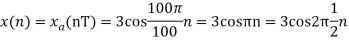
b. If 
, the discrete time signal is
c. If Fs=75Hz , the discrete time signal is
d. For the sampling rate 
in part in (c). Hence
So, the analog sinusoidal signal is
Q9) Suppose a continuous-time signal x(t) = cos (Ø0t) is sampled at a sampling frequency of 1000Hz to produce x[n]: x[n] = cos(πn/4). Determine 2 possible positive values of Ø0, say, Ø1and Ø2. Discuss if cos(Ø1t) or cos(Ø2t) will be obtained when passing through the DC converter.
A9)
Taking T= 1/1000s
Cos(πn/4) =x[n] = x(nT) = cos (Ø0n/1000)
Ø1is easily computed as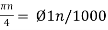 
Ø1 = 250π
Ø2 can be obtained by noting the periodicity of a sinusoid:
Ø2n/1000)
Ø2 = 2250π
Q10) Explain Sampling Theorem?
A10)
In sampling the signal m(t) is multiplied with periodic pulse train. Let M(ω) the spectrum of the input signal be band limited with the maximum frequency of fm as shown in figure 1.
Figure: 1 Spectrum of input Signal
Figure: 2 (fs>2 fm)
Figure: 3 (fs<2 fm)
The frequency spectrum of this signal when impulse sampled is plotted in figure 2 (for fs>2 fm). In figure 3 for (fs<2 fm). From figure 2 and figure 3 we can conclude that as long as fs≥2fm the original signal is preserved in the sampled signal and can be extracted from it by the low pass filter. This is known as Shannon’s Sampling theorem. This theorem states that the information contained in a signal is fully preserved in the sampled form as long as the sampling frequency is at least twice the maximum frequency contained in the signal.
