undefined | unit 1 power flow analysis

PS2

Unit - 1

Power Flow Analysis

Q1) Define the structure of Power System?

A1) An electric power system is usually understood as a very large network that links power plants (large or small) to loads, by means of an electric grid that may span a whole continent. A power system thus typically extends from a power plant right up to the sockets inside customers’ premises. These are sometimes referred to as full power systems as they are autonomous. Smaller power systems could be made of part or sections of a larger, full system. Figure 1 shows several elements that operate together and are connected to a power supplying network.

Power systems that are supplied by an external electricity source or that produce (by conversion from other sources) electricity and convey it to a larger grid are called partial power systems. The power systems that are of interest for our purposes are the large scale, full power systems that span large distances and have been deployed over decades by power companies.

Generation is the production of electricity at power stations or generating units where a form of primary energy is converted into electricity. Transmission is the network that moves power from one part of a country or a region to another. It is usually a well-interconnected infrastructure in which multiple power lines link different substations, which change voltage levels, offering enhanced redundancy.

Distribution finally delivers the power (we could say locally when compared to the transmission system) to the final loads (a majority of which are supplied at low voltage) via intermediate steps at which the voltage is converted down (transformed) to lower levels.

Q2) What are the components in a Power System?

A2)

(a) Synchronous Generators

The synchronous generators used in generating stations are revolving field type owing to its inherent advantages. The synchronous generators, based on the type of prime movers to which they are mechanically coupled, may be classified as:

(i) Hydro-generators

(ii) Turbo-generators, and

(iii) Diesel engine driven generators.

(b) Power Transformers

Power transformers are used for stepping-up the voltage for transmission at generating stations and for stepping-down voltage for further distribution at main step-down transformer substations. Usually naturally cooled, oil immersed, known as ON type, two winding, three-phase transformers, are used up to the rating of 10 MVA. The transformers of rating higher than 10 MVA are usually air blast cooled. For very high rating, the forced oil, water cooling and air blast cooling may be used. For regulating the voltage, the transformers used are provided with on load tap changer. They are put in operation during load hours and disconnected during light load hours i.e., they are usually operated at approximately full load. This is possible because they are arranged in banks and can be thrown in parallel with other units or disconnected at will. So, power transformers are designed to have maximum efficiency at or near full load (i.e., with iron loss to full-load copper loss ratio of 1: 1).

A switch is used for opening and closing of an electric circuit while a fuse is used for over-current protection. Every electric circuit needs a switching device and protective device. Switching and protective devices have been developed in different forms. Switchgear is a general term covering a wide range of equipment concerned with switching and protection. In a power system switchgear serves two basic purposes- (i) Switching during normal operating conditions for the purpose of operation and maintenance. (ii) Switching during abnormal conditions such as short-circuits and interrupting the fault currents.

(d) Bus-Bars

Bus-bar (or bus in short) term is used for a main bar or conductor carrying an electric current to which many connections may be made. Bus-bars are merely convenient means of connecting switches and other equipment into various arrangements. The usual arrangement of connections in most of the substations permits working on almost any piece of equipment without interruption to incoming or outgoing feeders. In some arrangements two buses are provided to which the incoming or outgoing feeders and the principal equipment may be connected. One bus is usually called the “main” bus and the other “auxiliary” or “transfer” bus. The main bus may have a more elaborate system of measuring instruments, relays etc. associated with it. The switches used for connecting feeders or equipment to one bus or the other are called “selector” or “transfer” switches.

Bus-bars may be of copper, aluminium or steel. Copper has a comparatively low resistivity and also the advantage of relatively high mechanical strength; this makes it economical to use copper bus-bars in installations of very large capacity where the currents are particularly heavy.

(e) Lightning Arrestors

The lightning arrester is a surge diverter and is used for the protection of power system against the high voltage surges. It is connected between the line and earth and so diverts the incoming high voltage wave to the earth. Lightning arresters act as safety valves designed to discharge electric surges resulting from lightning strokes, switching or other disturbances, which would otherwise flash-over insulators or puncture insulation, resulting in a line outage end possible failure of equipment.

Q3) Define Radial Type Topology in Distribution System?

A3) Radial Topology

Radial lines are used to connect primary substations (PSs) with secondary substations (SSs), and the SSs among them. These MV lines or “feeders” can be used exclusively for one SS or can be used to reach several of them. Radial systems keep central control of all the SSs.

Q4) Define Ring Type Topology in Distribution System?

A4) Ring Topology

This is a fault-tolerant topology to overcome the weakness of radial topology when there is a disconnection of one element of the MV line that interrupts electricity service (outage) in the rest of the connected substations. A ring topology is an improved evolution of the radial topology, connecting substations to other MV lines to create redundancy. Independently of the physical configuration, the grid is operated radially, but on the event of a failure in a feeder, other elements are maneuvered to reconfigure the grid in such a way that outages are avoided.

Q5) What is Network Topology?

A5) Networked topology consists of primary and secondary substations connected through multiple MV lines to provide a variety of distribution alternatives. Thus, the reconfiguration options to overcome faults are multiple, and in the event of failure, alternative solutions may be found to reroute electricity. LV grids present more complex and heterogeneous topologies than MV grids. The exact topology of LV systems depends on the extension and specific features of the service area, the type, number and density of points of supply (loads), country-specific and utility-specific operating procedures, and range of options in international standards.

An SS typically supplies electricity to one or several LV lines, with one or multiple MV-to-LV transformers at the same site. LV topology is typically radial, having multiple branches that connect to extended feeders, but there are also cases of networked grids and even ring or dual-fed configurations in LV networks.LV lines are typically shorter than MV lines, and their characteristics are different depending on the service area.

Q6) Derive the equation for Real & Reactive Power Flow?

A6) The admittance matrix of a power system is an abstract mathematical model of the system. It consists of admittance values of both lines and buses. The Y-bus is a square matrix with dimensions equal to the number of buses. This matrix is symmetrical along the diagonal-

The values of diagonal elements are equal to the sum of the admittances connected to bus ‘’. The off-diagonal elements are equal to the negative of the admittance connecting the two busses &, Y-bus is parse matrix-

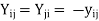
The net injected power at any bus can be calculated using the bus voltage (), neighboring bus voltages (), and admittances between the bus and its neighboring buses () as shown in the figure below-

The power equation at any bus can be written as follows:

Substituting the expression on the current in equation results in the following formula-

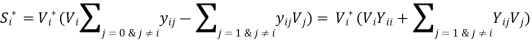
Real & Reactive Power can be calculated from the following equations-

Q7) Using Gauss-Seidel method derive the equation for power flow?

A7) Consider bus of a power system network as shown in figure below. Transmission lines are represented by equivalent π models where impedances have been converted to per unit admittances on a common MVA base.

Apply KCL to get the results;

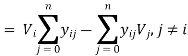
The real & reactive power at bus ‘i’ is

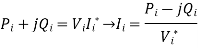
From this relationship, the mathematical formulation of the power flow problem results in a system of algebraic nonlinear equations which must be solved by iterative techniques.

In power flow study, it is essential to solve the set of non-linear equations for two unknown variables at each node. In Gauss-Seidel method, Vi is solved and the iterative sequences become-

Where,

is the actual admittance in per unit

are the net real & reactive powers in per unit

In KCL, current entering bus i was assumed positive. Thus, for buses where real and reactive powers are injected into the bus, such as generator buses, have positive values. For load buses where real and reactive powers are flowing away from the bus i, have negative values.

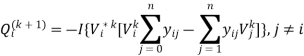
Rewriting the power flow equation in terms of the bus admittance matrix (Y-bus). Since the off-diagonal elements of the bus admittance matrix Ybus shown by uppercase letters, Yij = -yij the diagonal elements are Yii = ∑yij, the equation becomes-

For P-Q buses (load buses), & 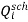are known. Starting with an initial estimate is solved for the real & imaginary components of voltage. For P-V buses (regulated buses), & |Vi| are specified, is solved, then used in . Since |Vi| is specified, only imaginary part of is retained. And its real part is selected in order to satisfy-

Where, & are the real & imaginary components of the voltage in the iterative sequence.

The rate of convergence is increased by applying acceleration factor- α to the approximate solution obtained from each iteration.

Α is the acceleration factor & it is in the range of 1.3 to 1.7. The process is continued until changes in the real & imaginary components of bus voltages between successive iterations are within specified accuracy.

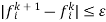
A voltage in accuracy is in the range of 0.00001 to 0.00005 per unit is satisfactory. • In practice, the method for determining the completion of a solution is based on an accuracy index set up on the power mismatch. The iteration continues until the magnitude of the largest element in the ΔP & ΔQ columns in less than specified value. Normally mismatch accuracy is 0.001 per unit. After solving for bus voltages & angles, power flows & losses in the network branches are calculated.

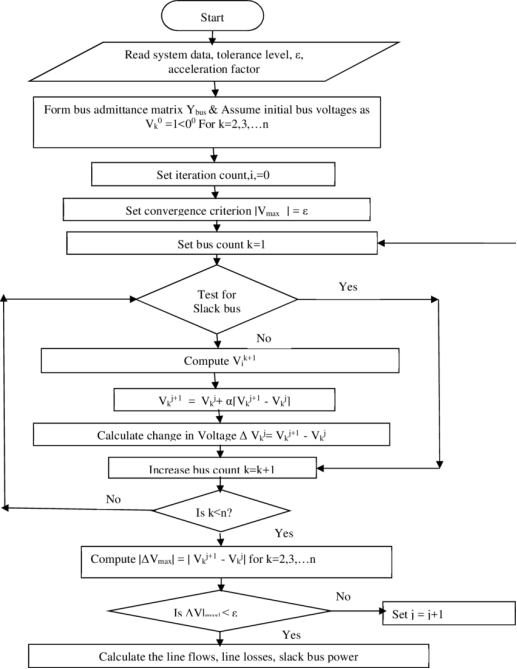
Q8) Draw the flowchart for Gauss Seidel method?

A8)

Flow-chart-for-load-flow-solution-using-Gauss-Seidel-method-Hadi-2010.png

Q9) Derive the equation of Power Flow using Newton Raphson method?

A9) Load flow solution is an unavoidable tool for power system planning and operation. NR and its derivatives are the most popular and widely used ones among the various methods of load flow solution techniques. In NR method one of the generator buses is treated as slack bus which is kept out of calculation during iterations. This is because of the fact that the slack bus is to carry entire loss of the system and total loss cannot be calculated before the end of iterations [8]. The exclusion of slack bus from the load flow iteration restricts many analyses to make. Consideration of distributed slack bus, load flow for Micro grids, study on minimization of system losses etc. cannot be performed when the slack bus is excluded from the iterations.

The results obtained from this analysis comprises the real and reactive power flow on transmission lines, reactive powers on generator buses, magnitudes and phase angles of load bus voltages. NR method of load flow analysis is an iterative method which approximates the set of nonlinear simultaneous equations to a set of linear simultaneous equations using Taylor’s series expansion and the terms are limited to first order approximation. The non-linear equations governing the power system network are:

Where, Si is the complex power in bus i

Vi is the bus voltage at bus i given as

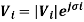and

Where, = is the bus angle at node i

e is the Euler’s constant

is the complex voltage at node i

Also

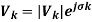Where Vk is the voltage at bus k

is the bus angle at node k

Ii is the current injected into bus i, given by

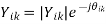
Where Yik is the admittance at bus I & k

Qik is the admittance angle at nodes i & k

Pi & Qi is the real & reactive power respectively at bus i

Separate the conjugate complex power in to real & imaginary power & we will get

The above equations constitute the polar form of the power flow equations that provide the calculated values for the net real power Pi & reactive power Qi entering the bus i. Denoting the calculated values of Pi by Pi cal and Qi by Qi cal leads to definition of mismatches ΔPi & ΔQi

Q10) Draw the flow chart of Newton Raphson Method?

A10)

Q11) What are the application of Newton Raphson method?

A11)

Newton-Raphson method can be used to optimally design water distribution network.

NR method is used in solving transcendental equations

It is used solve minimization & maximization problems

It is used for numerical verification for solutions of nonlinear equations

It is used to obtain zeroes of special functions

It is used to find the reciprocal of a number using only multiplication & subtraction

Q12) How can we implement Bus Admittance Matrix in Power System?

A12)

The amount of current present in the bus can be calculated with help of formation of Admittance matrix. I-Bus= Y-Bus * V-Bus. The voltages are measured with respect to ground & this equation is called nodal current equation

It is a vector equation consisting of ‘n’ scalar equations. I-bus is the vector of injected bus current (i.e., external current sources and Y-bus is the bus admittance matrix.

The diagonal element of each node is the sum of the admittances connected to it and is known as self-admittance or driving point admittance.

The off-diagonal element is equal to the negative of the admittance between the nodes. It is known as the mutual admittance or transfer admittance.

The Y-bus is a sparse matrix. For a large power system, more than 90% of off-diagonal elements are zero. This is due to the fact that in power system network, each node/bus is connected to not more than three nodes.

V-bus is the vector bus voltages measured from the reference node (i.e., node voltages).

Q13) What are the computational issues in large scale power system?

A13)

Decentralization- Information currently captured and consumed in a single regional power system will increasingly need to be visible to neighboring power systems and perhaps even visible on a national scale.

Scalability- Every smart grid concept we’ve reviewed brings huge numbers of new controllable entities to the table. In some ideas, every consumer’s home or office becomes an independent point for potential SCADA control. In others, the homes and offices behave autonomously but still must tap into dynamic data generated by the power provider, such as pricing or load predictions. Other ideas integrate enormous numbers of small power producing entities into the grid and require non‐trivial control adjustments to keep the grid stable. Thus, scalability will be a key requirement – scalability of a kind that dwarfs what the industry has done up to now, and demands a shift to new computational approaches.

Time Criticality- Some kinds of information need to be fresh. For example, studies have shown that correct SCADA systems can malfunction when presented with stale data, and some studies have even shown that SCADA systems operated over Internet standards like the ubiquitous TCP/IP protocols can malfunction, because out‐of‐the‐box TCP delays data for purposes of flow control and to correct data loss. Future smart‐grid solutions will demand real‐time response even in the presence of failures.

Consistency- Some kinds of information will need to be consistent, in the sense that if multiple devices are communicating with a SCADA system at the same time, they should be receiving the same instructions, even if they happen to connect to the SCADA system over different network paths that lead to different servers that provide the control information. Notice that we’re not saying that control data must be computed in some sort of radically new, decentralized manner: the SCADA computation itself could be localized, just as today’s cloud systems often start with one copy of a video of an important news event. But the key to scalability is to replicate data and computation, and consistency issues arise when a client platform requests data from a service replica: is this really the most current version of the control policy? Further, notice that consistency and real‐time guarantees are in some ways at odds. If we want to provide identical data to some set of clients, failures may cause delays: we lose real‐time guarantees of minimal delay. If we want minimal delay, we run the risk that a lost packet or a sudden crash could leave some clients without the most recent data.

Data Security- Several kinds of data mentioned above might be of interest to criminals, terrorists, or entities seeking an edge in the power commodities market. Adequate protection will be a critical requirement of future SCADA systems.

Reliability- Power systems that lose their control layer, even briefly, are at grave risk of damage or complete meltdown. Thus, any SCADA solution for the future smart grid needs to have high reliability.

Ability to tolerate & compromise- The most critical subsystems and services may need to operate even while under attack by intruders, viruses, or when some servers are malfunctioning. The technical term for this form of extreme reliability is Byzantine Fault Tolerance; the area is a rich one and many solutions are known, but deployments are rare and little is known about their scalability.

Q14) Define the load specification of Buses?

A14) A bus in a power system is defined as the vertical line at which the several components of the power system like generators, loads, and feeders, etc., are connected. The buses in a power system are associated with four quantities. These quantities are the magnitude of the voltage, the phase angle of the voltage, active or true power and the reactive power.

In the load flow studies, two variables are known, and two are to be determined. Depends on the quantity to be specified the buses are classified into three categories generation bus, load bus and slack bus.

The table shown below shows the types of buses and the associated known and unknown value.

Q15) Define Slack Bus?

A15) Slack bus in a power system absorb or emit the active or reactive power from the power system. The slack bus does not carry any load. At this bus, the magnitude and phase angle of the voltage are specified. The phase angle of the voltage is usually set equal to zero. The active and reactive power of this bus is usually determined through the solution of equations.

The slack bus is a fictional concept in load flow studies and arises because the I2R losses of the system are not known accurately in advance for the load flow calculation. Therefore, the total injected power cannot be specified at every bus. The phase angle of the voltage at the slack bus is usually taken as reference or zero.

Q16) Define Generation Bus?

A16) This bus is also called the P-V bus, and on this bus, the voltage magnitude corresponding to generate voltage and true or active power P corresponding to its rating are specified. Voltage magnitude is maintained constant at a specified value by injection of reactive power. The reactive power generation Q and phase angle δ of the voltage are to be computed.

Q17) Define Load Bus?

A17) This is also called the P-Q bus and at this bus, the active and reactive power is injected into the network. Magnitude and phase angle of the voltage are to be computed. Here the active power P and reactive power Q are specified, and the load bus voltage can be permitted within a tolerable value, i.e., 5 %. The phase angle of the voltage, i.e., δ is not very important for the load.

Q18) What is the need of Admittance Matrix?

A18) Mathematical model and solution of electric network is the basis of modern power system analysis, i.e., in studies of power flow, fault analysis, and contingency analysis. Electric network is constituted of transmission lines, transformers, parallel or series capacitors, and other static elements. We can establish equivalent circuit of any complicated network and analyze it according to the AC circuit laws. The electric network is represented by the linear lumped parameter model: for studies at synchronous frequency. For electromagnetic transient analysis: the high frequency phenomena and wave processes should be considered and Equivalent circuits described by distributed parameters.

Q19) Define the Y-Parameter Matrix?

A19) Y-parameter matrix describes the behaviour of any linear electrical network that can be regarded as a black box with a number of ports. A port in this context is a pair of electrical terminals carrying equal and opposite currents into and out of the network, and having a particular voltage between them. The Y-matrix gives no information about the behaviour of the network when the currents at any port are not balanced in this way (should this be possible), nor does it give any information about the voltage between terminals not belonging to the same port. Typically, it is intended that each external connection to the network is between the terminals of just one port, so that these limitations are appropriate.

For a generic multi-port network definition, it is assumed that each of the ports is allocated an integer n ranging from 1 to N, where N is the total number of ports. For port n, the associated Y-parameter definition is in terms of the port voltage and port current, {\displaystyle V_{n}\,} Vn & In and {\displaystyle I_{n}\,} respectively.

For all ports the currents may be defined in terms of the Y-parameter matrix and the voltages by the following matrix equation: I=YV

{\displaystyle I=YV\,}where Y is an N × N matrix the elements of which can be indexed using conventional matrix notation. In general, the elements of the Y-parameter matrix are complex numbers and functions of frequency. For a one-port network, the Y-matrix reduces to a single element, being the ordinary admittance measured between the two terminals.

Q20) What is the difference between Bus Admittance Matrix and Bus Impedance matrix?

A20) There are many differences between Bus Admittance Matrix and Bus Impedance matrix and hence they find applications in different domains. let me list out a few of the differences here:

Ybus is a Sparse Matrix that is most of elements are zero and hence less memory is required for storage whereas Zbus is a full matrix and all elements are non-zero so more memory is required.

Load Flow Studies involve Nodal Analysis and we wish to find the node or bus voltage and hence while forming KCL equation admittance is a natural choice as compared to impedance.

Ybus can be easily formed using inspection Method whereas Zbus building algorithm is complicated.

Ybus can be easily modified in case of any changes in the power system such as addition of transmission line or removal of transmission line.

Mutual Impedances can be directly considered by the use of Singular Transformation Method of Ybus formation.

Zbus is used in fault analysis because diagonal elements represent Thevenin Impedances whereas diagonal elements of Ybus do not represent Thevenin Admittances.

Sign Up