Unit – 4
Transformers
Q1) What are magnetic material?
A1)
- Iron
- Steel (an alloy of iron)
- Nickel
- Cobalt
- Are easy to magnetise
- Easily lose their magnetism
- Are hard to magnetise
- Do not easily lose their magnetism
Q2) Compare paramagnetic, di-magnetic and ferromagnetic material.
A2) 1. Paramagnetic Materials.
The materials, which are not strongly attracted by a magnet, such as aluminium, tin, platinum, magnesium, manganese etc., are known as paramagnetic materials. Their relative permeability is small but positive.
Such materials are slightly magnetized when placed in a strong magnetic field and act in the direction of the magnetic field. In paramagnetic materials the individual atomic dipoles are oriented in a random fashion, as shown in Figure.

The resultant magnetic field is, therefore, negligible. When an external magnetic field is applied, the permanent magnetic dipoles orient themselves parallel to the applied magnetic field and give rise to a positive magnetization. Since the orientation of the dipoles parallel to the applied magnetic field is not complete, the magnetization is small. These materials have little application in the field of electrical engineering.
2. Diamagnetic Materials. The materials which are repelled by a magnet such as zinc, mercury, lead, sulphur, copper, silver, bismuth, wood etc., are known as diamagnetic materials.
Their permeability is slightly less than unity.
For example, the relative permeabilities of bismuth, copper and wood are 0.99983, 0.999995 and 0.9999995 respectively.
They are slightly magnetized when placed in a strong magnetic field and act in the direction opposite to that of applied magnetic field. In diamagnetic materials, the two relatively weak magnetic fields (one caused due to orbital revolution and other due to axial rotation) are in opposite directions and cancel each other. Permanent magnetic dipoles are absent in them.
3. Ferromagnetic Materials. Ferromagnetism may be thought of as a special case of para magnetism in which the individual spin magnetic moments are interacting or coupled. As with paramagnets, ferromagnets have strong and positive magnetic susceptibility. Ferromagnetism is possible only when atoms are arranged in a lattice and the atomic magnetic moments interact to align parallel with each other. This field is sufficient to magnetize the material to saturation. Unlike paramagnets, when the applied field is removed, they retain a component of magnetization in the direction of the applied field – they are “permanently” magnetized Ferromagnetic materials are of two types: (a) soft magnetic material and (b) hard magnetic materials.
Q3) Draw and explain BH curve.
A3)
The curve plotted between flux density B and magnetizing force H of a material is called magnetizing or B-H curve.
The shape of curve is non-linear. This indicates that relative permeability (µr = B / µ0H) of a material is not constant, but it varies.
B-H curves are extremely useful to analyse the magnetic circuit. If value of flux density and dimension of magnetic circuit is known than from B-H curve total ampere turn can be easily known.
Q4) Explain ideal transformer.
A4) An ideal transformer is one that has
Although an ideal transformer cannot be physically realized, yet its study provides a very powerful tool in the analysis of a practical transformer. In fact, practical transformers have properties that approach very close to an ideal transformer.

Consider an ideal transformer on no load i.e., the secondary is open-circuited as shown in the figure. Under such conditions, the primary is simply a coil of pure inductance.
When an alternating voltage V₁ is applied to the primary, it draws a small magnetizing current Iₘ which lags behind the applied voltage by 90°. This alternating current Iₘ produces an alternating flux ϕ which is proportional to and in phase with it.
The alternating flux ϕ links both the windings and induces e.m.f. E₁ in the primary and e.m.f. E₂ in the secondary. The primary e.m.f. E₁ is, at every instant, equal to and in opposition to V₁ (Lenz’s law). Both e.m.f.sE₁, and E₂ lag behind flux ϕ by 90°. However, their magnitudes depend upon the number of primary and secondary turns.
Phasor Diagram of Ideal Transformer
The phasor diagram of an ideal transformer on no load is also shown above. Since flux ϕ is common to both the windings, it has been taken as the reference phasor.
The primary e.m.f. E₁ and secondary e.m.f. E₂ lag behind the flux ϕ by 90°.
Note that E₁ and E₂ are in phase. But E₁ is equal to V₁ and 180° out of phase with it.
Q5) Write short note on: iron losses, leakage reactance.
A5) Iron Losses
Since the iron core is subjected to alternating flux, there occurs eddy current and hysteresis loss in it. These two losses together are known as iron losses or core losses.
The iron losses depend upon the supply frequency, the maximum flux density in the core, volume of the core, etc.
It may be noted that the magnitude of iron losses is quite small in a practical transformer.
Leakage reactances
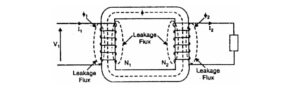
Both primary and secondary currents produce flux. The flux ϕ which links both the windings is the useful flux and is called mutual flux.
However, the primary current would produce some flux ϕ which would not link the secondary winding. Similarly, the secondary current would produce some flux ϕ that would not link the primary winding.
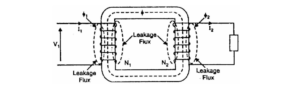
The flux such as ϕ₁ or ϕ₂ which links only one winding is called leakage flux. The leakage flux paths are mainly through the air. The effect of these leakage fluxes would be the same as though inductive reactance were connected in series with each winding of the transformer that had no leakage flux as shown in the figure.
In other words, the effect of primary leakage flux ϕ₁ is to introduce an inductive reactance X₁ in series with the primary winding as shown. Similarly, the secondary leakage flux ϕ₂ introduces an inductive reactance X₂ in series with the secondary winding.
There will be no power loss due to leakage reactance. However, the presence of leakage reactance in the windings changes the power factor as well as there is voltage loss due to IX drop.
Q6) Explain losses in a transformer.
A6) There are 2 types of losses occurring in a transformer
A) 1. Core loss or Iron loss
B) 2. Copper loss
Core losses:



Hysteresis loss : The iron loss occurring in the core of T/F due to the Hysteresis curve of the magnetic material used for core is called as Hysteresis loss.
Hysteresis curve is the curve as loop which shows the properly of magnetic material to lag the flux density B behind the field Intensely H

Above is the 3 different loops (Hysteresis of 3 diff. Materials)
 the selection of magnetic material for the construction of core depends upon Hysteresis loop of that material having tall and narrow Hysteresis loop is selected for the T/F core
the selection of magnetic material for the construction of core depends upon Hysteresis loop of that material having tall and narrow Hysteresis loop is selected for the T/F core
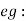 silicon Steel
silicon Steel
Hysteresis loss depends on fold factor
PH = KH. Bm1.67 F  V – watts
V – watts
Where KH = constant (Hyst)
Bm = max Flux density
F = Frequency
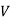 = Volume of core.
= Volume of core.
Reedy current loss :
This loss is due to the flow of reedy (circular) current in the core caused by induced emf in core
PE = Ke Bm2 f2 t2 v – watts
Where
Ke = reedy current const.
t = thickness of core
It can be reduced by using stacks of laminations instead of solid core
B] Copper loss : PCU
The Copper loss is due to resistance of the primary and secondary winding
It is load dependent / current dependent loss
As load on a transformer is variable (changing)  current changes
current changes  copper loss is a variable loss
copper loss is a variable loss
Primary secondary
Total C is loss = I12R12 + I22 R22
Copper loss depends upon load on T/F and is proportional to square of load current or KVA rating of transformer
 PCU
PCU 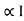 2
2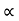 (KVA)2
(KVA)2
F.L = full load
 PCU (at half load) =
PCU (at half load) = 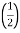 2 PCu F.L
2 PCu F.L
= (0.5)2 PCU F.L.
Or PCu (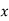 load) = (
load) = (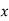 )2 PCu F.L
)2 PCu F.L
Q7) A 400 kVA transformer has a primary winding resistance of 0.5 ohm and a secondary winding resistance of 0.001 ohm. The iron loss is 2.5 Kw and the primary and secondary voltages are 5 kV and 320 V respectively. If the power factor of the load is 0.85, determine the efficiency of the transformer (i) on full load and (ii) on half load.
A7) Rated output = 400 kVA = 400x103 kVA
Full load secondary current, I2 = Rated output/V2 = 1250 A
Total resistance referred to secondary, re2 = r2+r1(V2/V1)2 = 0.033 ohm Full load copper loss, Pc = I22 re2 = 51.5625 Kw
Iron loss, Pi = 2.5 x103 watts
(i) Transformer efficiency at full load and 0.85 pf
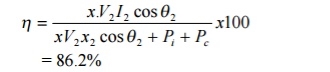
= 86.2%
(ii) Transformer efficiency at half load and 0.85 pf
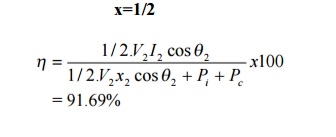
= 91.69%
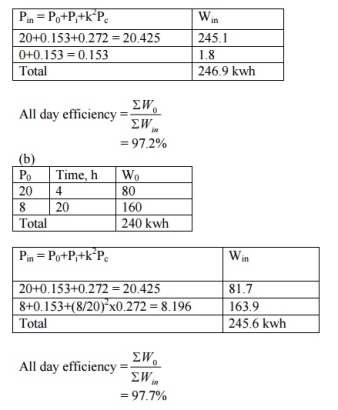
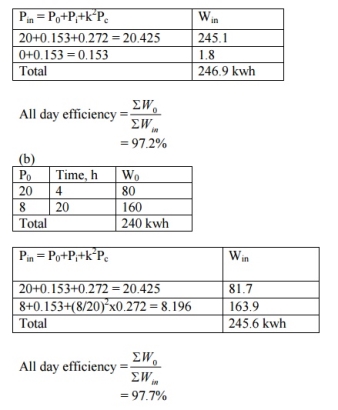
Q8) Find all day efficiency of a transformer having maximum efficiency of 98% at 15 kVA at unity power factor. Compare its all day efficiencies for the following load cycles:
a. Full load of 20 kVA, 12 hours per day and no load rest of the day. b. Full load, 4 hours per day and 0.4 full load rest of the day.
Assume the load to operate on upf all day
A8)

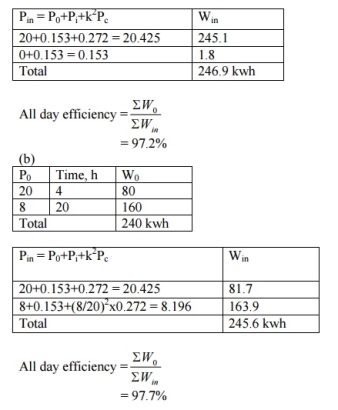
Unit – 4
Unit – 4
Transformers
Q1) What are magnetic material?
A1)
- Iron
- Steel (an alloy of iron)
- Nickel
- Cobalt

- Are easy to magnetise
- Easily lose their magnetism
- Are hard to magnetise
- Do not easily lose their magnetism
Q2) Compare paramagnetic, di-magnetic and ferromagnetic material.
A2) 1. Paramagnetic Materials.
The materials, which are not strongly attracted by a magnet, such as aluminium, tin, platinum, magnesium, manganese etc., are known as paramagnetic materials. Their relative permeability is small but positive.
Such materials are slightly magnetized when placed in a strong magnetic field and act in the direction of the magnetic field. In paramagnetic materials the individual atomic dipoles are oriented in a random fashion, as shown in Figure.

The resultant magnetic field is, therefore, negligible. When an external magnetic field is applied, the permanent magnetic dipoles orient themselves parallel to the applied magnetic field and give rise to a positive magnetization. Since the orientation of the dipoles parallel to the applied magnetic field is not complete, the magnetization is small. These materials have little application in the field of electrical engineering.
2. Diamagnetic Materials. The materials which are repelled by a magnet such as zinc, mercury, lead, sulphur, copper, silver, bismuth, wood etc., are known as diamagnetic materials.
Their permeability is slightly less than unity.
For example, the relative permeabilities of bismuth, copper and wood are 0.99983, 0.999995 and 0.9999995 respectively.
They are slightly magnetized when placed in a strong magnetic field and act in the direction opposite to that of applied magnetic field. In diamagnetic materials, the two relatively weak magnetic fields (one caused due to orbital revolution and other due to axial rotation) are in opposite directions and cancel each other. Permanent magnetic dipoles are absent in them.
3. Ferromagnetic Materials. Ferromagnetism may be thought of as a special case of para magnetism in which the individual spin magnetic moments are interacting or coupled. As with paramagnets, ferromagnets have strong and positive magnetic susceptibility. Ferromagnetism is possible only when atoms are arranged in a lattice and the atomic magnetic moments interact to align parallel with each other. This field is sufficient to magnetize the material to saturation. Unlike paramagnets, when the applied field is removed, they retain a component of magnetization in the direction of the applied field – they are “permanently” magnetized Ferromagnetic materials are of two types: (a) soft magnetic material and (b) hard magnetic materials.
Q3) Draw and explain BH curve.
A3)
The curve plotted between flux density B and magnetizing force H of a material is called magnetizing or B-H curve.
The shape of curve is non-linear. This indicates that relative permeability (µr = B / µ0H) of a material is not constant, but it varies.
B-H curves are extremely useful to analyse the magnetic circuit. If value of flux density and dimension of magnetic circuit is known than from B-H curve total ampere turn can be easily known.
Q4) Explain ideal transformer.
A4) An ideal transformer is one that has
Although an ideal transformer cannot be physically realized, yet its study provides a very powerful tool in the analysis of a practical transformer. In fact, practical transformers have properties that approach very close to an ideal transformer.

Consider an ideal transformer on no load i.e., the secondary is open-circuited as shown in the figure. Under such conditions, the primary is simply a coil of pure inductance.
When an alternating voltage V₁ is applied to the primary, it draws a small magnetizing current Iₘ which lags behind the applied voltage by 90°. This alternating current Iₘ produces an alternating flux ϕ which is proportional to and in phase with it.
The alternating flux ϕ links both the windings and induces e.m.f. E₁ in the primary and e.m.f. E₂ in the secondary. The primary e.m.f. E₁ is, at every instant, equal to and in opposition to V₁ (Lenz’s law). Both e.m.f.sE₁, and E₂ lag behind flux ϕ by 90°. However, their magnitudes depend upon the number of primary and secondary turns.
Phasor Diagram of Ideal Transformer
The phasor diagram of an ideal transformer on no load is also shown above. Since flux ϕ is common to both the windings, it has been taken as the reference phasor.
The primary e.m.f. E₁ and secondary e.m.f. E₂ lag behind the flux ϕ by 90°.
Note that E₁ and E₂ are in phase. But E₁ is equal to V₁ and 180° out of phase with it.
Q5) Write short note on: iron losses, leakage reactance.
A5) Iron Losses
Since the iron core is subjected to alternating flux, there occurs eddy current and hysteresis loss in it. These two losses together are known as iron losses or core losses.
The iron losses depend upon the supply frequency, the maximum flux density in the core, volume of the core, etc.
It may be noted that the magnitude of iron losses is quite small in a practical transformer.
Leakage reactances
Both primary and secondary currents produce flux. The flux ϕ which links both the windings is the useful flux and is called mutual flux.
However, the primary current would produce some flux ϕ which would not link the secondary winding. Similarly, the secondary current would produce some flux ϕ that would not link the primary winding.
The flux such as ϕ₁ or ϕ₂ which links only one winding is called leakage flux. The leakage flux paths are mainly through the air. The effect of these leakage fluxes would be the same as though inductive reactance were connected in series with each winding of the transformer that had no leakage flux as shown in the figure.
In other words, the effect of primary leakage flux ϕ₁ is to introduce an inductive reactance X₁ in series with the primary winding as shown. Similarly, the secondary leakage flux ϕ₂ introduces an inductive reactance X₂ in series with the secondary winding.
There will be no power loss due to leakage reactance. However, the presence of leakage reactance in the windings changes the power factor as well as there is voltage loss due to IX drop.

Q6) Explain losses in a transformer.
A6) There are 2 types of losses occurring in a transformer
A) 1. Core loss or Iron loss
B) 2. Copper loss
Core losses:



Hysteresis loss : The iron loss occurring in the core of T/F due to the Hysteresis curve of the magnetic material used for core is called as Hysteresis loss.
Hysteresis curve is the curve as loop which shows the properly of magnetic material to lag the flux density B behind the field Intensely H
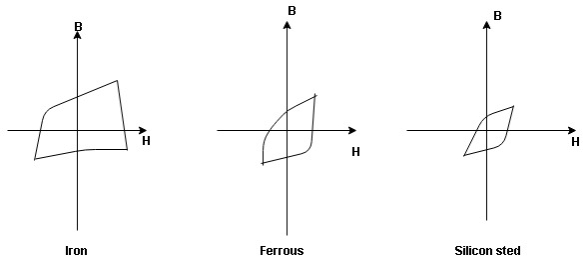
Above is the 3 different loops (Hysteresis of 3 diff. Materials)
 the selection of magnetic material for the construction of core depends upon Hysteresis loop of that material having tall and narrow Hysteresis loop is selected for the T/F core
the selection of magnetic material for the construction of core depends upon Hysteresis loop of that material having tall and narrow Hysteresis loop is selected for the T/F core
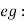 silicon Steel
silicon Steel
Hysteresis loss depends on fold factor
PH = KH. Bm1.67 F 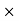 V – watts
V – watts
Where KH = constant (Hyst)
Bm = max Flux density
F = Frequency
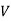 = Volume of core.
= Volume of core.
Reedy current loss :
This loss is due to the flow of reedy (circular) current in the core caused by induced emf in core
PE = Ke Bm2 f2 t2 v – watts
Where
Ke = reedy current const.
t = thickness of core
It can be reduced by using stacks of laminations instead of solid core
B] Copper loss : PCU
The Copper loss is due to resistance of the primary and secondary winding
It is load dependent / current dependent loss
As load on a transformer is variable (changing)  current changes
current changes  copper loss is a variable loss
copper loss is a variable loss
Primary secondary
Total C is loss = I12R12 + I22 R22
Copper loss depends upon load on T/F and is proportional to square of load current or KVA rating of transformer
 PCU
PCU 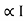 2
2 (KVA)2
(KVA)2
F.L = full load
 PCU (at half load) =
PCU (at half load) = 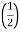 2 PCu F.L
2 PCu F.L
= (0.5)2 PCU F.L.
Or PCu (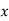 load) = (
load) = (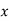 )2 PCu F.L
)2 PCu F.L
Q7) A 400 kVA transformer has a primary winding resistance of 0.5 ohm and a secondary winding resistance of 0.001 ohm. The iron loss is 2.5 Kw and the primary and secondary voltages are 5 kV and 320 V respectively. If the power factor of the load is 0.85, determine the efficiency of the transformer (i) on full load and (ii) on half load.
A7) Rated output = 400 kVA = 400x103 kVA
Full load secondary current, I2 = Rated output/V2 = 1250 A
Total resistance referred to secondary, re2 = r2+r1(V2/V1)2 = 0.033 ohm Full load copper loss, Pc = I22 re2 = 51.5625 Kw
Iron loss, Pi = 2.5 x103 watts
(i) Transformer efficiency at full load and 0.85 pf
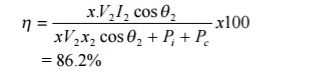
= 86.2%
(ii) Transformer efficiency at half load and 0.85 pf

= 91.69%
Q8) Find all day efficiency of a transformer having maximum efficiency of 98% at 15 kVA at unity power factor. Compare its all day efficiencies for the following load cycles:
a. Full load of 20 kVA, 12 hours per day and no load rest of the day. b. Full load, 4 hours per day and 0.4 full load rest of the day.
Assume the load to operate on upf all day
A8)

Unit – 4
Transformers
Q1) What are magnetic material?
A1)
- Iron
- Steel (an alloy of iron)
- Nickel
- Cobalt
- Are easy to magnetise
- Easily lose their magnetism
- Are hard to magnetise
- Do not easily lose their magnetism
Q2) Compare paramagnetic, di-magnetic and ferromagnetic material.
A2) 1. Paramagnetic Materials.
The materials, which are not strongly attracted by a magnet, such as aluminium, tin, platinum, magnesium, manganese etc., are known as paramagnetic materials. Their relative permeability is small but positive.
Such materials are slightly magnetized when placed in a strong magnetic field and act in the direction of the magnetic field. In paramagnetic materials the individual atomic dipoles are oriented in a random fashion, as shown in Figure.

The resultant magnetic field is, therefore, negligible. When an external magnetic field is applied, the permanent magnetic dipoles orient themselves parallel to the applied magnetic field and give rise to a positive magnetization. Since the orientation of the dipoles parallel to the applied magnetic field is not complete, the magnetization is small. These materials have little application in the field of electrical engineering.
2. Diamagnetic Materials. The materials which are repelled by a magnet such as zinc, mercury, lead, sulphur, copper, silver, bismuth, wood etc., are known as diamagnetic materials.
Their permeability is slightly less than unity.
For example, the relative permeabilities of bismuth, copper and wood are 0.99983, 0.999995 and 0.9999995 respectively.
They are slightly magnetized when placed in a strong magnetic field and act in the direction opposite to that of applied magnetic field. In diamagnetic materials, the two relatively weak magnetic fields (one caused due to orbital revolution and other due to axial rotation) are in opposite directions and cancel each other. Permanent magnetic dipoles are absent in them.
3. Ferromagnetic Materials. Ferromagnetism may be thought of as a special case of para magnetism in which the individual spin magnetic moments are interacting or coupled. As with paramagnets, ferromagnets have strong and positive magnetic susceptibility. Ferromagnetism is possible only when atoms are arranged in a lattice and the atomic magnetic moments interact to align parallel with each other. This field is sufficient to magnetize the material to saturation. Unlike paramagnets, when the applied field is removed, they retain a component of magnetization in the direction of the applied field – they are “permanently” magnetized Ferromagnetic materials are of two types: (a) soft magnetic material and (b) hard magnetic materials.
Q3) Draw and explain BH curve.
A3)
The curve plotted between flux density B and magnetizing force H of a material is called magnetizing or B-H curve.
The shape of curve is non-linear. This indicates that relative permeability (µr = B / µ0H) of a material is not constant, but it varies.
B-H curves are extremely useful to analyse the magnetic circuit. If value of flux density and dimension of magnetic circuit is known than from B-H curve total ampere turn can be easily known.
Q4) Explain ideal transformer.
A4) An ideal transformer is one that has
Although an ideal transformer cannot be physically realized, yet its study provides a very powerful tool in the analysis of a practical transformer. In fact, practical transformers have properties that approach very close to an ideal transformer.

Consider an ideal transformer on no load i.e., the secondary is open-circuited as shown in the figure. Under such conditions, the primary is simply a coil of pure inductance.
When an alternating voltage V₁ is applied to the primary, it draws a small magnetizing current Iₘ which lags behind the applied voltage by 90°. This alternating current Iₘ produces an alternating flux ϕ which is proportional to and in phase with it.
The alternating flux ϕ links both the windings and induces e.m.f. E₁ in the primary and e.m.f. E₂ in the secondary. The primary e.m.f. E₁ is, at every instant, equal to and in opposition to V₁ (Lenz’s law). Both e.m.f.sE₁, and E₂ lag behind flux ϕ by 90°. However, their magnitudes depend upon the number of primary and secondary turns.
Phasor Diagram of Ideal Transformer
The phasor diagram of an ideal transformer on no load is also shown above. Since flux ϕ is common to both the windings, it has been taken as the reference phasor.
The primary e.m.f. E₁ and secondary e.m.f. E₂ lag behind the flux ϕ by 90°.
Note that E₁ and E₂ are in phase. But E₁ is equal to V₁ and 180° out of phase with it.
Q5) Write short note on: iron losses, leakage reactance.
A5) Iron Losses
Since the iron core is subjected to alternating flux, there occurs eddy current and hysteresis loss in it. These two losses together are known as iron losses or core losses.
The iron losses depend upon the supply frequency, the maximum flux density in the core, volume of the core, etc.
It may be noted that the magnitude of iron losses is quite small in a practical transformer.
Leakage reactances
Both primary and secondary currents produce flux. The flux ϕ which links both the windings is the useful flux and is called mutual flux.
However, the primary current would produce some flux ϕ which would not link the secondary winding. Similarly, the secondary current would produce some flux ϕ that would not link the primary winding.
The flux such as ϕ₁ or ϕ₂ which links only one winding is called leakage flux. The leakage flux paths are mainly through the air. The effect of these leakage fluxes would be the same as though inductive reactance were connected in series with each winding of the transformer that had no leakage flux as shown in the figure.
In other words, the effect of primary leakage flux ϕ₁ is to introduce an inductive reactance X₁ in series with the primary winding as shown. Similarly, the secondary leakage flux ϕ₂ introduces an inductive reactance X₂ in series with the secondary winding.
There will be no power loss due to leakage reactance. However, the presence of leakage reactance in the windings changes the power factor as well as there is voltage loss due to IX drop.
Q6) Explain losses in a transformer.
A6) There are 2 types of losses occurring in a transformer
A) 1. Core loss or Iron loss
B) 2. Copper loss
Core losses:



Hysteresis loss : The iron loss occurring in the core of T/F due to the Hysteresis curve of the magnetic material used for core is called as Hysteresis loss.
Hysteresis curve is the curve as loop which shows the properly of magnetic material to lag the flux density B behind the field Intensely H
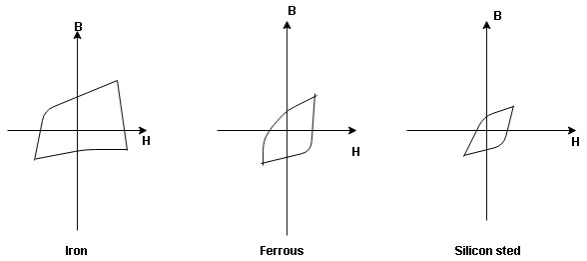
Above is the 3 different loops (Hysteresis of 3 diff. Materials)
 the selection of magnetic material for the construction of core depends upon Hysteresis loop of that material having tall and narrow Hysteresis loop is selected for the T/F core
the selection of magnetic material for the construction of core depends upon Hysteresis loop of that material having tall and narrow Hysteresis loop is selected for the T/F core
 silicon Steel
silicon Steel
Hysteresis loss depends on fold factor
PH = KH. Bm1.67 F 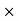 V – watts
V – watts
Where KH = constant (Hyst)
Bm = max Flux density
F = Frequency
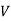 = Volume of core.
= Volume of core.
Reedy current loss :
This loss is due to the flow of reedy (circular) current in the core caused by induced emf in core
PE = Ke Bm2 f2 t2 v – watts
Where
Ke = reedy current const.
t = thickness of core
It can be reduced by using stacks of laminations instead of solid core
B] Copper loss : PCU
The Copper loss is due to resistance of the primary and secondary winding
It is load dependent / current dependent loss
As load on a transformer is variable (changing)  current changes
current changes  copper loss is a variable loss
copper loss is a variable loss
Primary secondary
Total C is loss = I12R12 + I22 R22
Copper loss depends upon load on T/F and is proportional to square of load current or KVA rating of transformer
 PCU
PCU 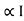 2
2 (KVA)2
(KVA)2
F.L = full load
 PCU (at half load) =
PCU (at half load) = 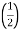 2 PCu F.L
2 PCu F.L
= (0.5)2 PCU F.L.
Or PCu (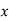 load) = (
load) = ( )2 PCu F.L
)2 PCu F.L
Q7) A 400 kVA transformer has a primary winding resistance of 0.5 ohm and a secondary winding resistance of 0.001 ohm. The iron loss is 2.5 Kw and the primary and secondary voltages are 5 kV and 320 V respectively. If the power factor of the load is 0.85, determine the efficiency of the transformer (i) on full load and (ii) on half load.
A7) Rated output = 400 kVA = 400x103 kVA
Full load secondary current, I2 = Rated output/V2 = 1250 A
Total resistance referred to secondary, re2 = r2+r1(V2/V1)2 = 0.033 ohm Full load copper loss, Pc = I22 re2 = 51.5625 Kw
Iron loss, Pi = 2.5 x103 watts
(i) Transformer efficiency at full load and 0.85 pf
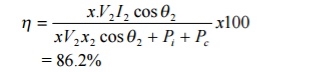
= 86.2%
(ii) Transformer efficiency at half load and 0.85 pf
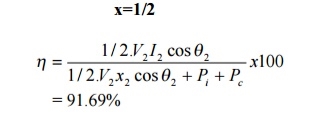
= 91.69%
Q8) Find all day efficiency of a transformer having maximum efficiency of 98% at 15 kVA at unity power factor. Compare its all day efficiencies for the following load cycles:
a. Full load of 20 kVA, 12 hours per day and no load rest of the day. b. Full load, 4 hours per day and 0.4 full load rest of the day.
Assume the load to operate on upf all day
A8)