Unit-5

Error

Q1) Explain the block diagram of PAM system?

A1)

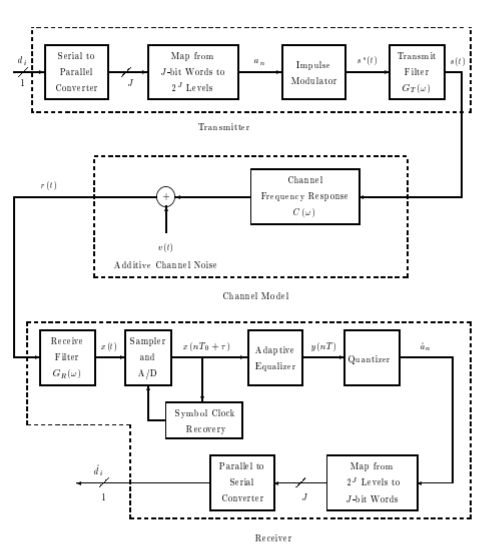
Fig 1 Baseband PAM Block Diagram

The transmitter input di is a serial binary data sequence with a bit rate of Rd bits/sec. Input bits are blocked into J-bit words by the serial-to-parallel converter. Input blocks are mapped into the sequence of symbols an which are selected from an alphabet of M = 2J distinct voltage levels. For example, the following levels uniformly spaced by 2d are commonly used:

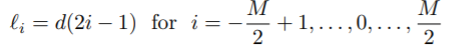
The minimum level is −(M − 1)d and the maximum level is (M − 1)d. The symbol rate is fs = 1/T = Rd/J symbols/sec

The impulse modulator output is

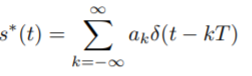
The band limiting transmit filter output is

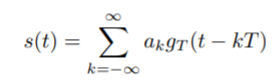
The channel is modelled as a filter C(ω) followed by an additive noise source. The receive filter eliminates out-of-band noise and, in conjunction with the transmit filter, forms a properly shaped pulse. The output of the receive filter is sampled at a rate that is an integer multiple N of the symbol rate fs. Typically, N might be 3 or 4. These samples are used by the Symbol Clock Recovery system to lock the receiver symbol clock to the transmitter clock.

The Adaptive Equalizer is an FIR filter with adjustable taps that automatically compensates for channel amplitude and phase distortion. It also corrects for small deviations in the transmit and receive filter responses from their ideal nominal values. A least mean-square error (LMS) adaptation algorithm is used most often. The equalizer output is sampled at the symbol rate and quantized to the nearest ideal level. The Quantizer output is mapped to the corresponding J-bit binary word and converted back to a serial output data sequence.

Q2) What is probability of error?

A2) The analysis for 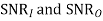assumes perfectly white noise j (t) for simplicity. Note that a white noise j(t) has infinite power such that j (t) and c(t)j(t) will have the same PSD

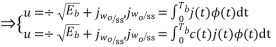
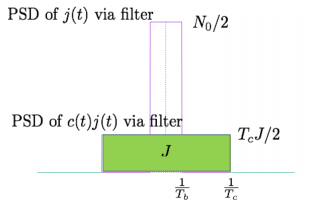
Fig 2 PDF Comparison

)

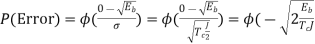Q3) Explain the function of optimal filter?

A3) An optimum filter is such a filter used for acquiring a best estimate of desired signal from noisy measurement. It is different from the classic filters. These filters are optimum because they are designed based on optimization theory to minimize the mean square error between a processed signal and a desired signal, or equivalently provides the best estimation of a desired signal from a measured noisy signal.

It is pervasive that when we measure a (desired) signal d(n), noise v(n) interferes with the signal so that a measured signal becomes a noisy signal

x(n) x(n)=d(n)+v(n)

It is also very common that a signal d(n) is distorted in its measurement (e.g., an electromagnetic signal distorts as it propagates over a radio channel). Assuming that the system causing distortion is characterized by an impulse response of h (n) s , the measurement of d(n) can be expressed by the sum of distorted signal s(n) and noise

v(n) x(n)=s(n)+v(n)= h (n)∗ s d(n)+v(n)

where s(n)= h (n)∗ s d(n).

If both d(n) and v(n) are assumed to be wide-sense stationary (WSS) random processes, then x(n) is also a WSS process. The signals that we discuss in this chapter will be WSS if they are not specially specified. If signal d(n) and measurement noise v(n) are assumed to be uncorrelated (this is true in many practical cases), then r (k) = r (k) = 0.

In this case, the noisy signal,

x(n)= h (n)∗ s d(n)+v(n),

the relation of r (k) x with r (k ) d and r (k) v (the autocorrelations of x(n), d(n) and v(n), respectively) as follows,

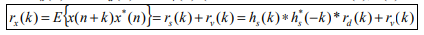
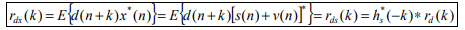
For the noisy signal of the form x(n)= d(n)+v(n), a special case of where h (n) s =δ (n) and no distortion happens to d(n) in its measurement, we have

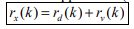
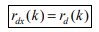
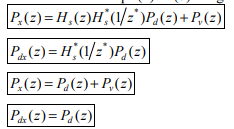
Optimum filtering is to acquire the best linear estimate of a desired signal from a measurement. The main issues in optimal filtering contain

• filtering that deals with recovering a desired signal d(n) from a noisy signal (or measurement) x(n);

• prediction that is concerned with predicting a signal d(n+m) for m>0 from observation x(n);

• smoothing that is an a posteriori form of estimation, i.e., estimating d(n+m) for m

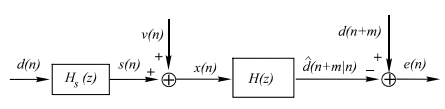
Fig 3 Optimum Filtering

Q4) Explain the working of matched filters?

A4) If a filter produces an output in such a way that it maximizes the ratio of output peak power to mean noise power in its frequency response, then that filter is called Matched filter.

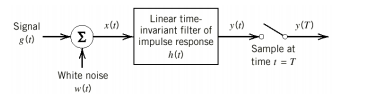
Fig 4 Matched Filter

Frequency Response Function of Matched Filter

The frequency response of the Matched filter will be proportional to the complex conjugate of the input signal’s spectrum. Mathematically, we can write the expression for frequency response function, H(f) of the Matched filter as −

H(f)=GaS∗(f)e−j2πft1    ………..1

Where,

Ga is the maximum gain of the Matched filter

S(f) is the Fourier transform of the input signal, s(t)

S∗(f) is the complex conjugate of S(f)

t1 is the time instant at which the signal observed to be maximum

In general, the value of Ga is considered as one. We will get the following equation by substituting Ga=1in Equation 1.

H(f)=S∗(f)e−j2πft1  ……..2

The frequency response function, H(f) of the Matched filter is having the magnitude of S∗(f)and phase angle of e−j2πft1, which varies uniformly with frequency.

Q5) What is impulse response of matched filters?

A5) In time domain, we will get the output, h(t) of Matched filter receiver by applying the inverse Fourier transform of the frequency response function, H(f).

h(t)=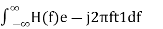 ….….3

Substitute, Equation 1 in Equation 3.

h(t)=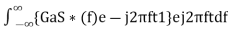

⇒h(t)=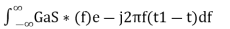 ………4

We know the following relation.

S∗(f)=S(−f)                                   ……..5

Substitute, Equation 5 in Equation 4.

h(t)=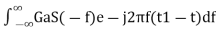

⇒h(t)=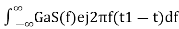

⇒h(t)=Gas(t1−t)

In general, the value of Ga is considered as one. We will get the following equation by substituting Ga=1.

h(t)=s(t1−t)

The above equation proves that the impulse response of Matched filter is the mirror image of the received signal about a time instant t1. The following figures illustrate this concept.

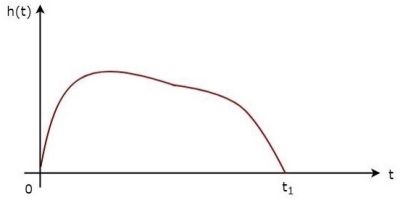
Fig 5 Impulse Response of Matched Filter

The received signal, s(t) and the impulse response, h(t) of the matched filter corresponding to the signal, s(t) are shown in the above figures.

Q6) Derive the expression for probability of error in matched filter?

A6)

Q7) What is coherent reception explain?

A7) Coherent detection is well known in wireless communication systems. In those wireless systems, a radio frequency (RF) local oscillator (LO) is tuned to “heterodyne”, which is a signal processing technique which combine a high-frequency signal  f1 with another  f2 to produce a lower frequency signal (f1 – f2), with a received signal through an RF mixer, as shown in Fig.(a), so that both the amplitude and phase information contained in an RF carrier can be recovered in the following digital signal processor (DSP).

For an optical coherent system, a narrow-linewidth tunable laser, serving as an LO, tunes its frequency to “intradyne” with a received signal frequency through an optical coherent mixer, as shown in Fig. (b), and thereby recovers both the amplitude and phase information contained in a particular optical carrier.

Here, “intradyne” means that the frequency difference between an LO and a received optical carrier is small and within the bandwidth of the receiver, but does not have to be zero. 

This implies that the frequency and phase of an LO do not have to be actively controlled to an extreme accuracy, therefore avoiding the use of a complicated optical phase locked loop.

Fig 6 (a) RF Mixer (b) Optical Coherent mixer

In contrast to coherent detection is direct detection, typically used by 10Gb/s or lower-speed systems.  In a direct detection receiver, its photo-detector only responds to changes in the receiving signal optical power, and cannot extract any phase or frequency information from the optical carrier.

Q8) What are the advantages of coherent detection?

A8) Advantages of Coherent detection:

(2) Can extract amplitude, frequency, and phase information from an optical carrier, and consequently can achieve much higher capacity in the same bandwidth.

(3) Its DSP can compensate very large chromatic and polarization mode dispersion due to optical fibers, and eliminate the need for optical dispersion compensators and the associated optical amplifiers.

(4) When using balanced detectors with a high common mode noise rejection ratio (CMRR), not only signal-to-noise ratio (SNR) can be improved further, but also agile wavelength selection can be achieved by LO tuning without the use of an optical filter or demultiplexer.

Q9) Explain non-coherent detection of ASK?

A9) Incoherent detection as used in analog communication does not require carrier for reconstruction. The simplest form of incoherent detector is the envelope detector as shown in figure below. The output of envelope detector is the baseband signal. Once the baseband signal is recovered, its samples are taken at regular intervals and compared with threshold. If Z(t) is greater than threshold (  ) a decision will be made in favour of symbol ‘1’ If Z(t) the sampled value is less than threshold (  ) a decision will be made in favour of symbol ‘0’

Fig 7 Envelop detection for BASK

Q10) Explain non-coherent detection of FSK?

A10)

Fig 8 Non—Coherent Detection of FSK

Figure above shows the block diagram of incoherent type FSK demodulator. The detector consists of two band pass filters one tuned to each of the two frequencies used to communicate ‘0’s and ‘1’s., The output of filter is envelope detected and then baseband detected using an integrate and dump operation. The detector is simply evaluating which of two possible sinusoids is stronger at the receiver. If we take the difference of the outputs of the two envelope detectors the result is bipolar baseband. The resulting envelope detector outputs are sampled at t = kTb and their values are compared with the threshold and a decision will be made in favour of symbol 1 or 0.