Unit-1

Calculus

Question-1: Prove that the evolute of parabola 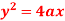is given by

Ans 1) It is given that-

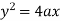
If (X,Y) are the coordinates of the centre of curvature at any point P(x , y) on the curve y = f(x), then X and Y are given as-

  …………….. (1)

Now consider the equation of parabola (given)

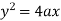
On differentiating w.r.t x-

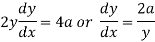
Again differentiating w.r.t.x-

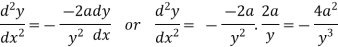
Put these derivatives in (1), we get-

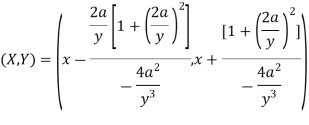
Now consider X,

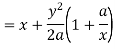
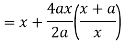
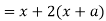
Here we get-

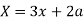
Now consider,

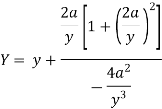
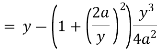
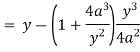
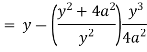
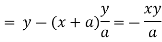
Here we get-

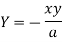
Now

Taking L.H.S of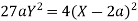

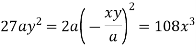
Taking R.H.S of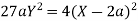

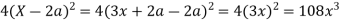
Hence proved.

Question-2: Find the evolute of the ellipse .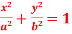

Ans 2) It is given that-

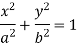
The parametric equations are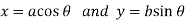

Now,

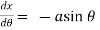  and 

So that-

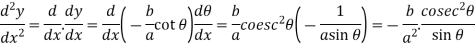
Which gives,

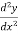
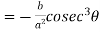
Co-ordinates of centre of curvature are (X , Y),

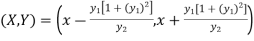  …………….. (1)

Consider X,

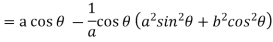
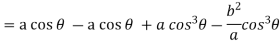
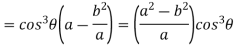
We get-

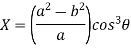
Now consider Y,

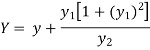
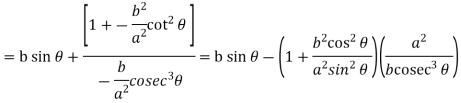
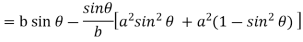
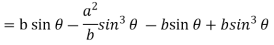
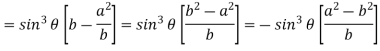
So that we get-

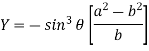
Eliminating 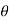from X and Y, we get,

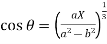       and      

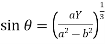
We know that

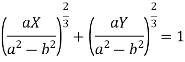
Which gives on solving-

Which is the required evolute.

Question-3: Evaluate.

Ans 3) Here we notice that  f:x→cos x  is a decreasing function on [a , b],

Therefore by the definition of the definite integrals-

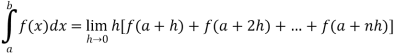
Then

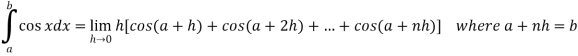
Now,

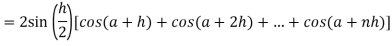
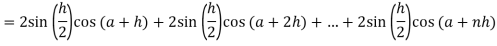
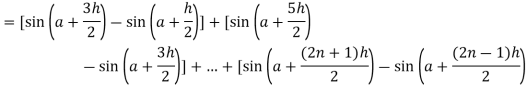
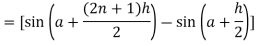
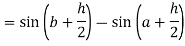
Here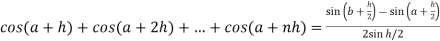

Thus

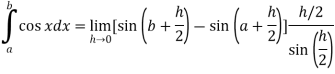
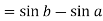
Question-4: Evaluate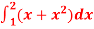

Ans 4) Here 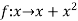is an increasing function on [1 , 2]

So that,

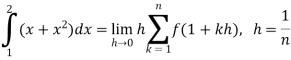
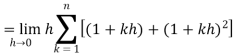
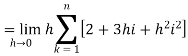
  …. (1)

We know that-

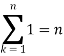
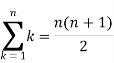
And

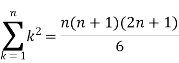
Then equation (1) becomes-

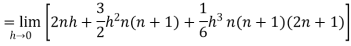
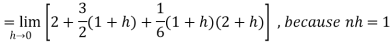
Question-5: Evaluate 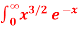dx

Ans 5)

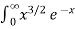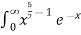dx = dx

= γ(5/2)

= γ (3/2+ 1)

= 3/2 γ(3/2 )

= 3/2.  ½ γ (½ )

= 3/2. ½ π

=    ¾ π

Question-6: Show that    

Ans 6)

=

=

= )  .......................

=

=

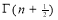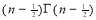
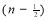
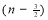
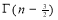
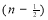
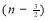
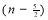
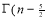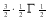
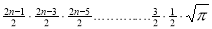
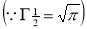
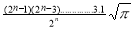
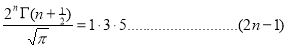
Question-7: Determine the area enclosed by the curves-

Ans 7) We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-

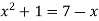
Which gives-

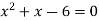
By factorization,

Which means,

x = 2 and x = -3

By determining the intersection points the range the values of x has been found-

x	-3	-2	-1	0	1	2
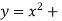1	10	5	2	1	2	5

And

We get the following figure by using above two tables-

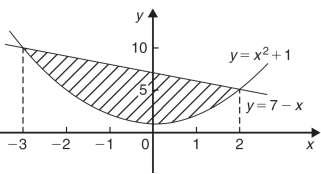
Area of shaded region =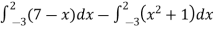

=

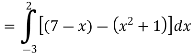
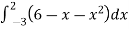
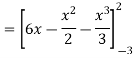
= ( 12 – 2 –  8/3 ) – (-18 – 9/2 + 9)

=

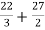
= 125/6 square unit

Question-8: Determine the area bounded by three straight lines y = 4 – x, y = 3x and 3y = x

Ans 8) We get the following figure by using the equations of three straight lines-

y = 4 – x, y = 3x and 3y = x

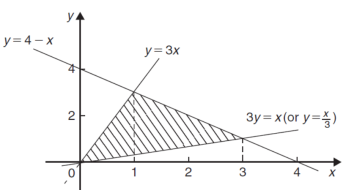
Area of shaded region-

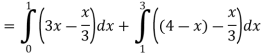
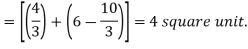
Qustion-9: Find the area enclosed by the two functions-

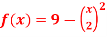and g(x) = 6 – x

Ans 9) We get the following figure by using these two equations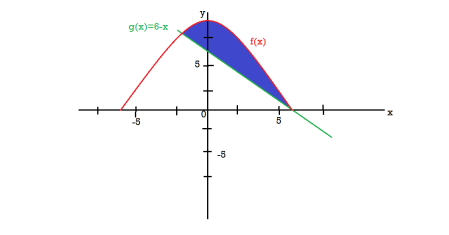                                 

To find the intersection points of two functions f(x) and g(x)-

f(x) = g(x)

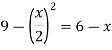
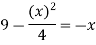
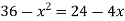
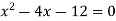
On factorizing, we get-

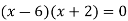
x = 6, -2

Now

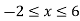
Then, area under the curve-

A =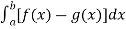

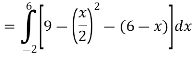
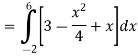
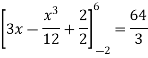
Therefore the area under the curve is  64/3  square unit.

Question-10: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].

Ans 10) The graph of the function f(x) = 1/x will look like-

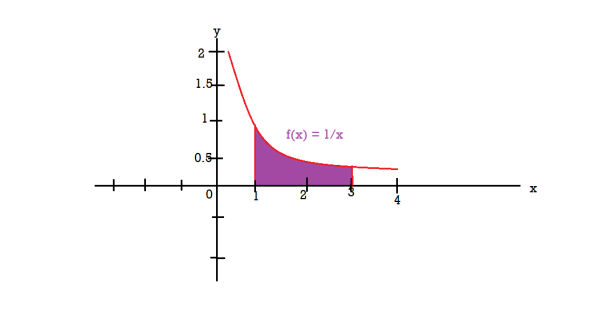
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]

Then the volume of the solid will be-