Unit-2

Calculus

Question-1: Verify Rolle’s theorem for the function f(x) = x(x+3) 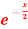in interval [-3, 0].

Ans 1) First we will differentiate the given function with respect to x, we get

f’(x) = (x²+3x) + (2x + 3)

=

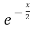
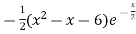
This shows that f’(x) exists for all x, therefore f(x) is continuous for all x.

Now, f(-3) = 0 and f(0) = 0 , so that f(-3) = f(0).

Here f(x) satisfies all the conditions of Rolle’s theorem,

Then,

f’(x) = 0  , which gives

= 0

We get,

X = 3 and x = -2

Here we can see that clearly -3<-2<0 , therefore there exists   -2 ∈ (-3,0) such that

f’(-2) = 0

That means the Rolle’s theorem is true for the given function.

Question-2: Verify the Rolle’s theorem for sin x in the interval []

Ans 2) Suppose f(x) = sin x

We know that sin x is continuous for all x.

Now , f’(x) = cos x exists for all x in (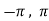) and

f(0

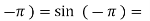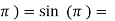f(0

thus f(x) satisfies all the conditions of Rolle’s theorem.

Now,

f’(x) = 0 that gives ,    cos x = 0

x =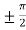  

Here we notice that both intervals lie in (.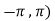

There exists, c =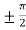

So that, f’(c) = 0

The Rolle’s theorem has been verified.

Question-3: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].

Ans 3) As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).

f(x) = (x-1)(x-2)(x-3)

f(x) =  x-6x²+11x-6

now at x = 0, we get

f(0) = -6  and

at x = 4, we get.

f(4) = 6

diff. the function w.r.t.x , we get

f’(x) = 3x²-6x+11

suppose x = c, we get

f’(c) = 3c²-6c+11

by Lagrange’s mean value theorem,

f’(c) = 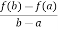   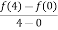 =  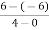   =   = 3

now we get,

3c²-6c+11 = 3

3c²-6c+8 = 0

On solving the quadratic equation, we get

C = 2

Here we see that the value of c lies between 0 and 4

Therefore the given function is verified.

Question-4: Verify Lagrange’s mean value theorem for f(x) = log xin [1,e].

Ans 4) We already know that the function which is log x is continuous for all x>0.

So that this is the continuous function In [1,e]

Now,

f’(x) = 1/x

which is exists for all x in (1,e)

so that f(x) is differentiable in (1,e).

by Lagrange’s mean value theorem, we get

f’(c) = , let x = c,

then ,

f’(c) =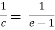

we get,

c = e-1

e-1 will always lies between 1 and e .

hence the function is verified by Lagrange’s mean value theorem.

Queestion-5: Verify Cauchy’s mean value theorem for the function f(x) = sin x and g(x) = cos x  in [ 0 , π/2]

Ans 5)  It is given tha,

f(x) = sin x and g(x) = cos x

Now,

  f’(x) = cos x and g’(x) = - sin x

We know that both the functions are continuous in [ 0 , π/2] and differentiable in     ( 0 , π/2 )

Also, g’(x) = -sin x  ≠ 0 for all x ϵ( 0 , π/2 )

By Cauchy’s mean value theorem, we get

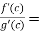
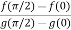       for some c: 0< c <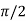

That means

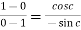  which gives,

Cot c = 1

C =

Now we see that lies between 0 and

Queston-6: Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]

Ans 6) We are given, f(x) = x⁴ and g(x) = x

Derivative of these fucntions ,

      f’(x) = 4x³ and g’(x) = 2x

put these values in Cauchy’s formula, we get

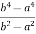
2c² =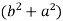

c² =

c =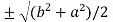

now put the values of a = 1 and b = 2 ,we get

c = 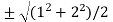= = 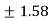(approx)

Hence the Cauchy’s theorem is verified.

Question-7: Expand sin x in powers of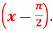

Ans 7) Let f(x) = sin x

     Then,

=

          By using Taylor’s theorem-

+ …….     (1)

Here f(x) = sin x and a = π/2

f’(x) = cos x  , f’’(x) = - sin x    ,     f’’’(x) = - cos x  and so on.

Putting x = π/2 , we get

f(x) = sin x = = 1

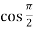f’(x) = cos x = = 0

f’’(x) = -sin x = 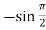= -1

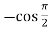f’’’(x) = -cos x = = 0

from equation (1) put a = and substitute these values, we get-

+ …….

= ………………………..

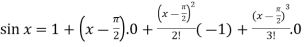Question-8: Evaluate .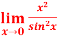

Ans 8) Let f(x) = 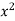and g(x) = .

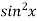Here we see that this is the indeterminate form of 0/0 at x = 0.

Now by using L’Hospital rule, we get-

=

=

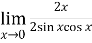
= = 1

Question-9: Evaluate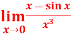

Ans 9) We can see that this is an indeterminate form of type 0/0.

Apply L’Hospital’s rule, we get

But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-

We get

=

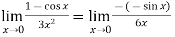Question-10: Find 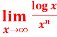  , n>0.

Ans 10) Let f(x) = log x and g(x) =

These two functions satisfied the theorem that we have discussed above-

So that,

Question-11: Find out the maxima and minima of the function

Ans 11)

Given 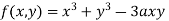    …(i)

Partially differentiating (i) with respect to x we get

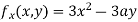    ….(ii)

Partially differentiating (i) with respect to y we get

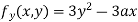    ….(iii)

Now, form the equations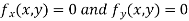

Using (ii) and (iii) we get

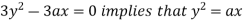
          using above two equations

Squaring both side we get

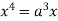
Or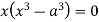 

This show that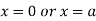

Also we get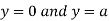

Thus we get the pair of value as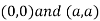

Now, we calculate

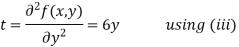
Putting above values in

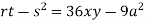
At point (0,0)  we get

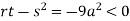
So, the point (0,0) is a saddle point.

At point 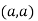we get

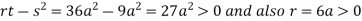
So the point 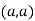is the minimum point where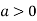

In case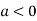 

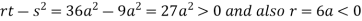
So the point 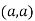is the maximum point where