UNIT-5

Matrices

Question-1: Find the inverse of matrix ‘A’ by using elementary transformation-

A =

Ans 1)  Write the matrix ‘A’ as-

A = IA

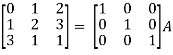
Apply , we get

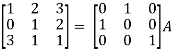
Apply

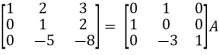
Apply

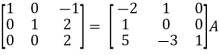
Apply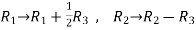

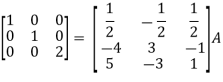
Apply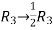

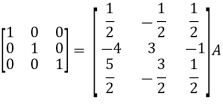
So that,

  =

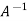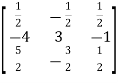
Question-2: Find the rank of a matrix A by echelon form.

A =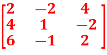

Ans 2) Convert the matrix A into echelon form,

A =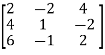

Apply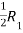 

A =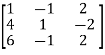

Apply 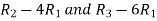   , we get

A =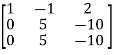

Apply 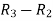, we get

A =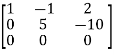

Apply ,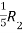

A =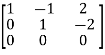

Apply  ,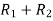

A =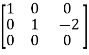

Therefore the rank of the matrix will be 2.

Question-3: Find the rank of a matrix A by echelon form.

A =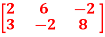

Ans 3) Transform the matrix A into echelon form, then find the rank,

We have,

A =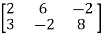

Apply,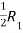 

A =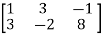

Apply ,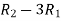

A =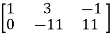

Apply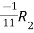

A =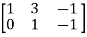

Apply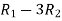

A =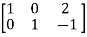

Hence the rank of the matrix will be 2.

Question-4: reduce the matrix A to its normal form and find rank as well.

Ans 4)  We have,

We will apply elementary row operation,

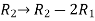
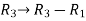
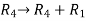
We get,

Now apply column transformation,

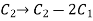
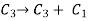
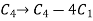
We get,

Apply

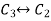  , we get,

Apply 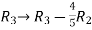  and

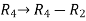
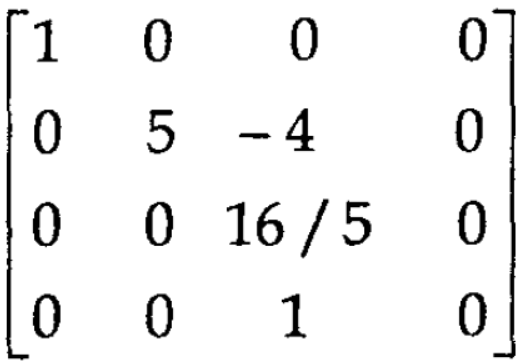
Apply 

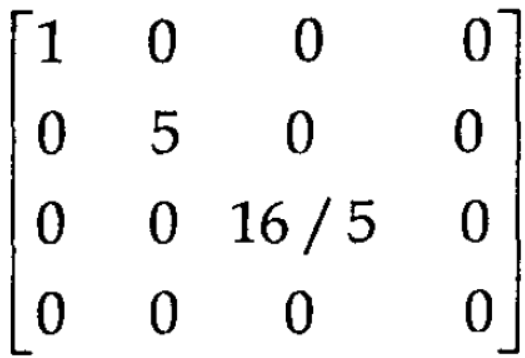
Apply   and

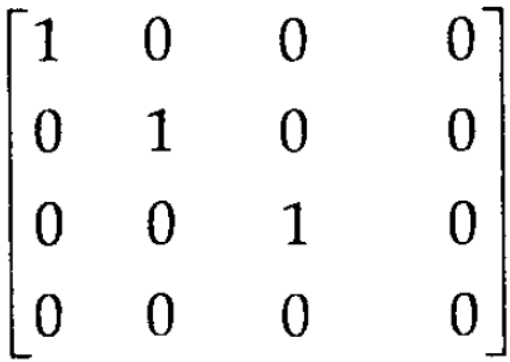
Apply   and

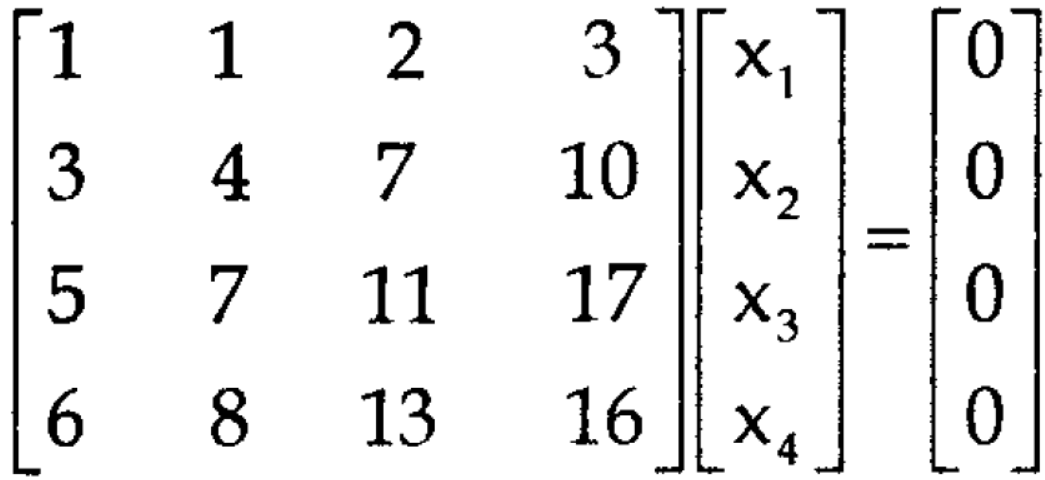
As we can see this is required normal form of matrix A.

Therefore the rank of matrix A is 3.

Question-5: Find the solution of the following homogeneous system of linear equations,

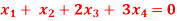
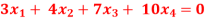
Ans 5) The given system of linear equations can be written in the form of matrix as follows,

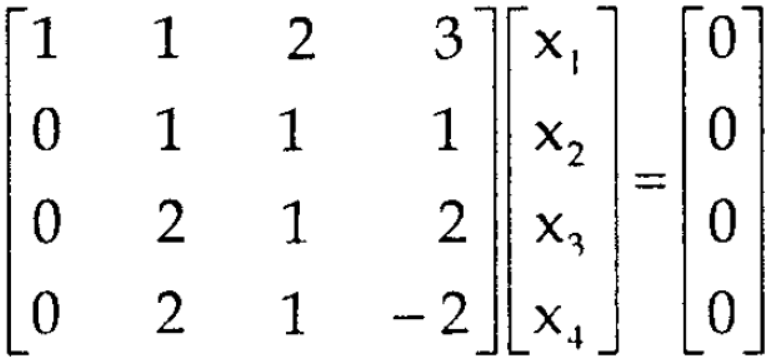
Apply the elementary row transformation,

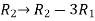
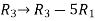
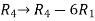  , we get,

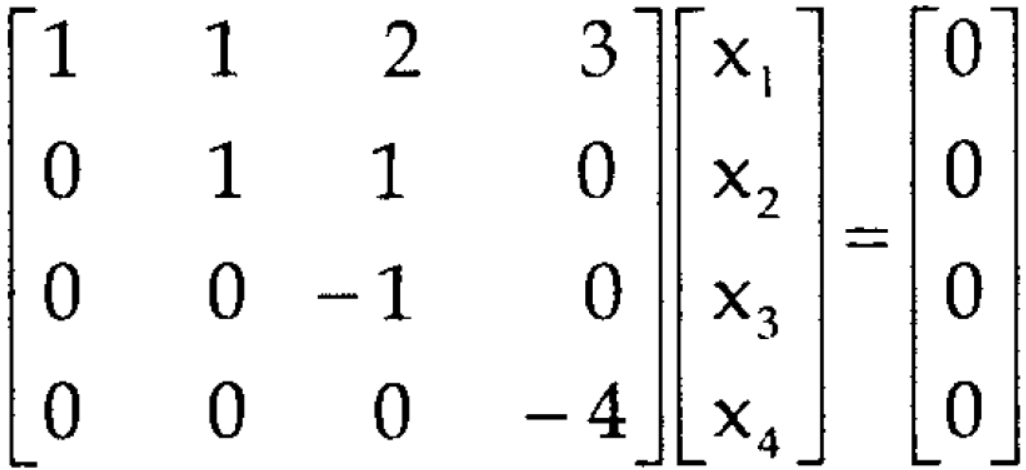
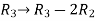
    , we get

Here r(A) = 4, so that it has trivial solution,

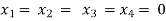
Question-6: Check the consistency and find the values of x , y and z of the following system of linear equations.

2x + 3y + 4z = 11

X + 5y + 7z = 15

3x + 11y + 13z = 25

Ans 6) Re-write the system of equations in augmented matrix form.

C = [A,B]

That will be,

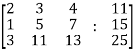
Apply 

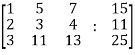
Now apply , 

We get,

  ~  ~

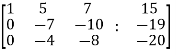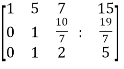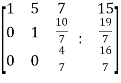
Here rank of A = 3

And rank of C = 3, so that the system of equations is consistent,

So that we can can solve the equations as below,

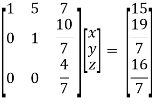
That gives,

x + 5y + 7z = 15  ……………..(1)

y + 10z/7 = 19/7 ………………(2)

4z/7 = 16/7 ………………….(3)

From eq. (3)

z = 4,

From 2,

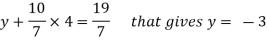
From eq.(1), we get

x + 5(-3) + 7(4) = 15

That gives,

x = 2

Therefore the values of x , y , z are    2 , -3 , 4  respectively.

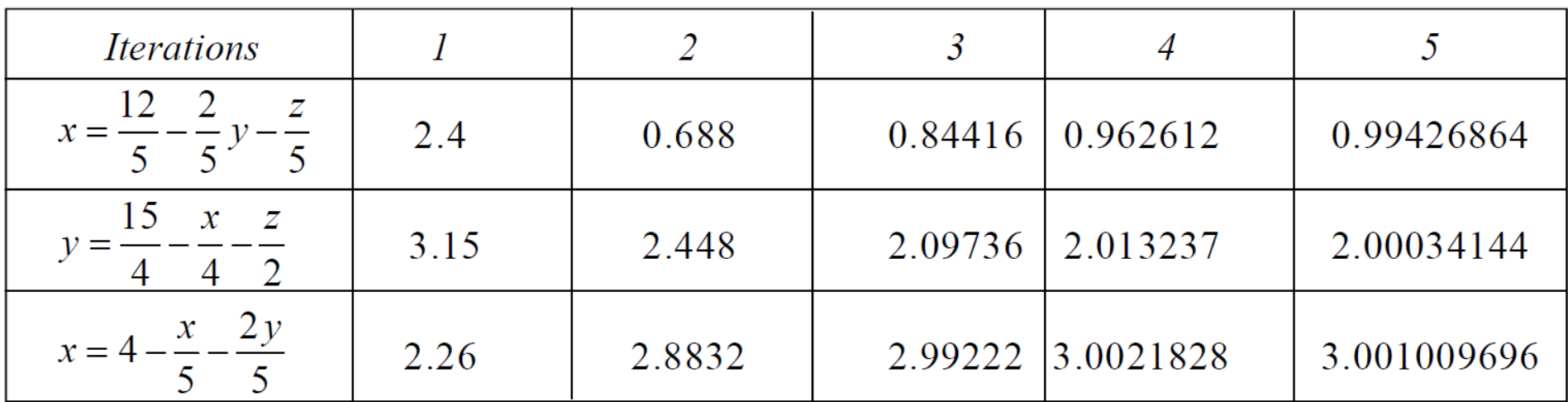
Question-7: Solve the following system of linear equations by using Guass Seidel method-

5x + 2y + z = 12

x + 4y + 2z = 15

x + 2y + 5z = 20

Ans 7) These equations can be written as ,

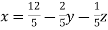   ………………(1)

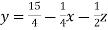………………………(2)

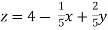   ………………………..(3)

Put y and z equals to 0 in eq. 1

We get,

x = 2.4

put x = 2.4, and z = 0 in eq. 2 , we get

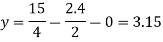
Put x = 2.4 and y = 3.15 in eq.(3) , we get

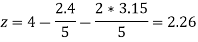
Again start from eq.(1), put the values of y and z , we get

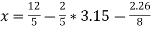= 0.688

We repeat the process again and again ,

The following table can be obtained –

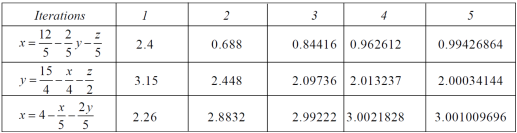
We see that the values are approx. equal to exact values.

Exact values are, x = 1, y = 2,   z = 3.

Question-8: Find the minors and cofactors of the first row of the determinant.

Ans 8)  (1)  The minor of element 2 will be,

Delete the corresponding row and column of element 2,

We get,

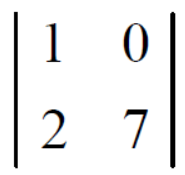
Which is equivalent to,     1 × 7 - 0 × 2 = 7 – 0 = 7

Similarly the minor of element 3 will be,

4× 7 - 0× 6 = 28 – 0 = 28

Minor of element 5,

4 × 2 - 1× 6 = 8 – 6 = 2

The cofactors of 2, 3 and 5 will be,

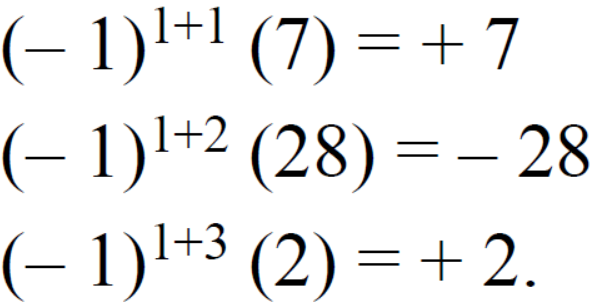
Question-9: prove that (without expanding) the determinant given below is equal zero.

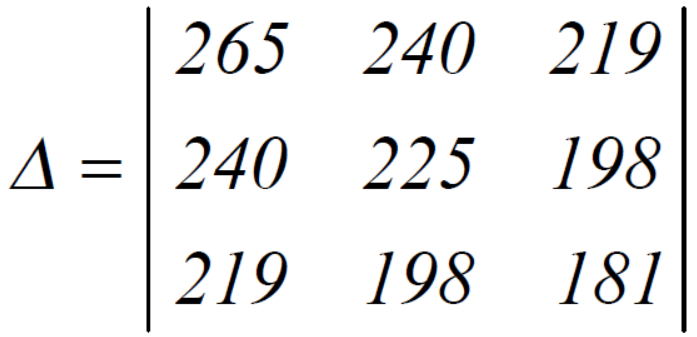
Ans 9)  Applying the operation,

We get,

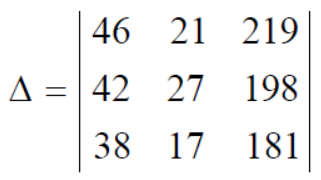
Now applying the operation,

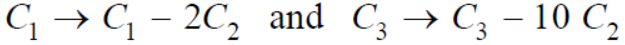
We get,

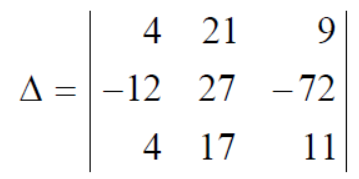
Apply,

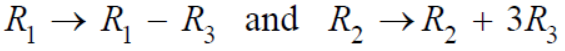
We get,

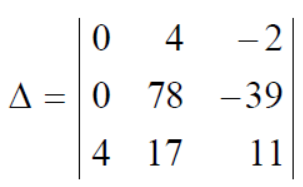
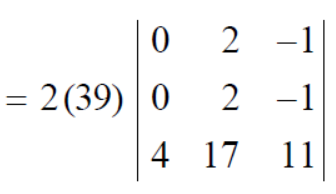
Here first and second row are identical then we know that by property it becomes zero.

Question-10: Show that the points given below are collinear-

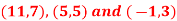
Ans 10)

First we need to find the area of these points and if the area is zero then we can say that these are collinear points-

So that-

We know that area enclosed by three points-

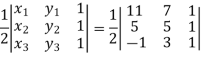
Apply-

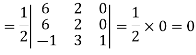
So that these points are collinear.

Question-11: Examine whether the following vectors are linearly independent or not.

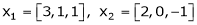and .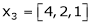

Ans 11)

Consider the vector equation,

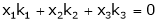
i.e. 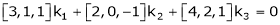  … (1)

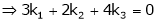
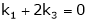
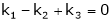
Which can be written in matrix form as,

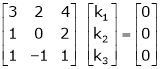
R12

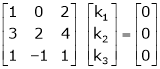
R2 – 3R1, R3 – R1

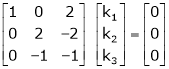
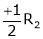
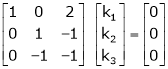
R3 + R2

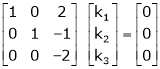
Here Rank of coefficient matrix is equal to the no. of unknowns. i.e. r = n = 3.

Hence the system has unique trivial solution.

i.e.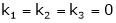

i.e. vector equation (1) has only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent.

Question-12: Find the Eigen values of Eigen vector for the matrix.

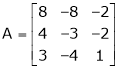
Ans 12)

Consider the characteristic equation as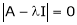

i.e.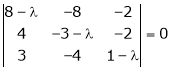

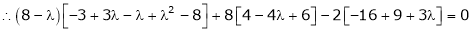
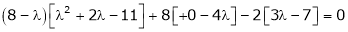
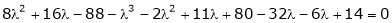
i.e.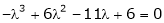

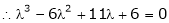
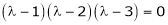
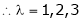are the required eigen values.

Now consider the equation

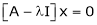       … (1)

Case I:

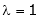Equation (1) becomes,

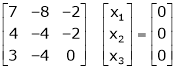
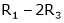
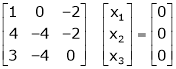
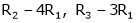
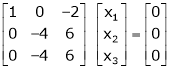
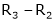
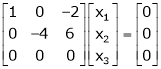
Thus 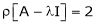and n = 3

3 – 2 = 1 independent variables.

Now rewrite the equations as,

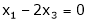
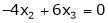
Put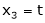

,

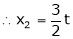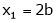
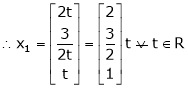
I.e.

the Eigen vector for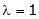

Case II:

If 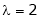equation (1) becomes,

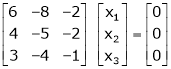
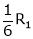
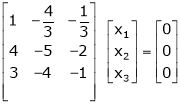
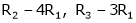
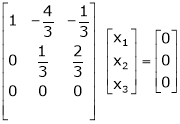
Thus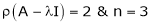

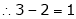
Independent variables.

Now rewrite the equations as,

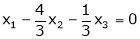
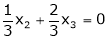
Put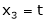

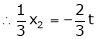
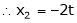
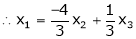
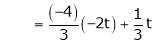
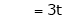
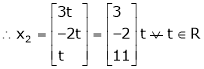
Is the Eigen vector for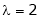

Now

Case III:-

If 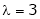equation (1) gives,

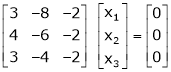
R1 – R2

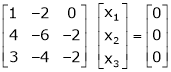
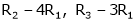
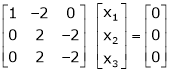
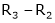
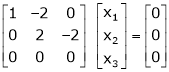
Thus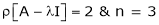

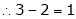
Independent variables

Now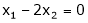

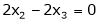
Put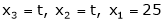

Thus

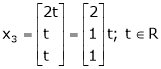
Is the Eigen vector for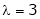

Question-13: Diagonalise the matrix

Ans 13)

Let A=

The three Eigen vectors obtained are  (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values .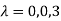

Then 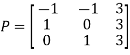   and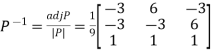

Also we know that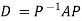    

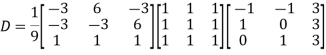
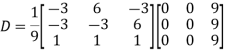
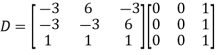
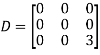
Question-14: Find the characteristic equation of the matrix A =   and Verify cayley-Hamlton theorem.

Ans 14) Characteristic equation of the matrix, we can be find as follows-

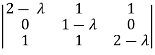
Which is,

( 2 -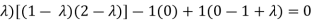  , which gives

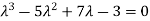
According to cayley-Hamilton theorem,

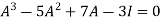  …………(1)

Now we will verify equation (1),

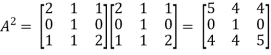
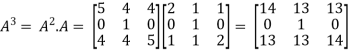
Put the required values in equation (1) , we get

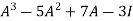
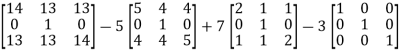
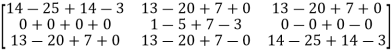
Hence the cayley-Hamilton theorem is verified.

Question-15: Using Cayley-Hamilton theorem, find , if A = ?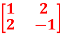

Ans 15) Let A =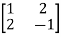

The characteristics equation of A is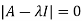

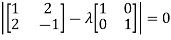
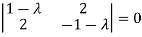
Or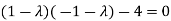

Or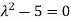

By Cayley-Hamilton theorem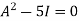   

L.H.S.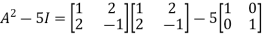

=

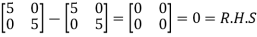
By Cayley-Hamilton theorem we have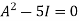   

Multiply both side by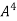

.

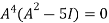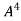
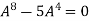
Or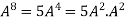 

=

=

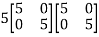
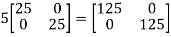
Question-16: If the matrix A defines an orthogonal transformation , then show that

+    ( i≠j)  i,j = 1 , 2 , 3.

Where

A =

Sol.  As we know that an orthogonal matrix A ,

AA’ = I = A’A     and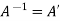 

We will find AA’,

AA’ =   =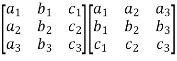

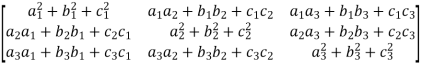
A will be orthogonal only if -    AA’ = I

In that case, it is only possible when,

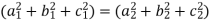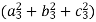= = 1

And,

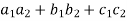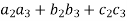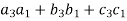() = () = () = 0