Unit 4

Unit 4

Algebraic structure and morphism

Q1) Consider an algebraic system (N, +), where the set N = {0, 1, 2, 3, 4...}.The set of natural numbers and + is an addition operation. Determine whether (N, +) is a monoid.

Solution: (a) Closure Property: The operation + is closed since the sum of two natural numbers.

(b)Associative Property: The operation + is an associative property since we have (a+b)+c=a+(b+c) ∀ a, b, c ∈ N.

(c)Identity: There exists an identity element in set N the operation +. The element 0 is an identity element, i.e., the operation +. Since the operation + is a closed, associative and there exists an identity. Hence, the algebraic system (N, +) is a monoid.

Q2) Let G be a permutation group on an infinite set X. There is a graded algebra A[G] associated with G as follows: the nth homogeneous component Vn is the set of all G-invariant functions from the set of n-element subsets of X to the complex numbers; multiplication is defined by the rule that, if f in Vn, g in Vm, and K is an (n+m)-element set then

(fg)(K) = sum f(L)g(K-L) : L subseteq K, |L| = n.

Solution :

The constant function e in V1 with value 1 is not a zero-divisor. We say that G is entire if A[G] is an integral domain, and strongly entire if A[G]/eA[G] is an integral domain. It is conjectured that G is (strongly) entire if and only if it has no finite orbits on X. In the absence of a proof of this conjecture, can one show the following:

If the permutation groups G1 on X1 and G2 on X2 are (strongly) entire, then G1 × G2 (in its intransitive action on X1 union X2) is (strongly) entire.

Q3) Find the truth value and from that information find the logically equivalent disjunctive normal form.

                 a. [(p  q)  r]                                                 b. P  (q  r)

Solution: a. (p  q  r) V (p  q  r) V (p  q  r)

                 b. (p  q  r) V (p  q  r) V (p  q  r) (circled false outputs)

Q4) Consider an algebraic system (G, *), where G is the set of all non-zero real numbers and * is a binary operation defined by

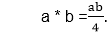
Show that (G, *) is an abelian group.

Solution:

Closure Property: The set G is closed under the operation *, since a * b = 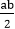 is a real number. Hence, it belongs to G.

Associative Property: The operation * is associative. Let a,b,c∈G, then we have

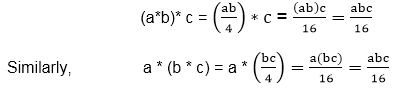
Identity: To find the identity element, let us assume that e is a +ve real number. Then e * a = a, where a ∈G.

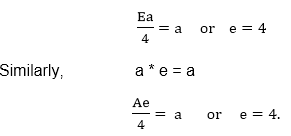
Thus, the identity element in G is 4.

Q5) Consider the lattice of all +ve integers I+ under the operation of divisibility. The lattice Dn of all divisors of n > 1 is a sub-lattice of I+.

Determine all the sub-lattices of D30 that contain at least four elements, D30={1,2,3,5,6,10,15,30}.

Solution: The sub-lattices of D30 that contain at least four elements are as follows:

1. {1, 2, 6, 30}          2. {1, 2, 3, 30}
3. {1, 5, 15, 30}          4. {1, 3, 6, 30}
5. {1, 5, 10, 30}          6. {1, 3, 15, 30}
7. {2, 6, 10, 30}

Q6) Write the dual of following Boolean expressions:

1. (x1*x2) + (x1*x3')         2. (1+x2)*( x1+1)
3. (a ∧(b∧c))

Solution:

1. ( x1+x2)*( x1+x3')         2. (0*x2)+( x1*0)
3. (a ∨(b∧c))

Q7) Simplify: AB(A + B)(B + B):

Q9)) Show that (2, 5) encoding function e B2 B5 defined by

e(00) = 01100e(10) = 10001

e (01) = 01110e(11) = 11011

Is a group code.

Unit 4

Unit 4

Algebraic structure and morphism

Q1) Consider an algebraic system (N, +), where the set N = {0, 1, 2, 3, 4...}.The set of natural numbers and + is an addition operation. Determine whether (N, +) is a monoid.

Solution: (a) Closure Property: The operation + is closed since the sum of two natural numbers.

(b)Associative Property: The operation + is an associative property since we have (a+b)+c=a+(b+c) ∀ a, b, c ∈ N.

(c)Identity: There exists an identity element in set N the operation +. The element 0 is an identity element, i.e., the operation +. Since the operation + is a closed, associative and there exists an identity. Hence, the algebraic system (N, +) is a monoid.

Q2) Let G be a permutation group on an infinite set X. There is a graded algebra A[G] associated with G as follows: the nth homogeneous component Vn is the set of all G-invariant functions from the set of n-element subsets of X to the complex numbers; multiplication is defined by the rule that, if f in Vn, g in Vm, and K is an (n+m)-element set then

(fg)(K) = sum f(L)g(K-L) : L subseteq K, |L| = n.

Solution :

The constant function e in V1 with value 1 is not a zero-divisor. We say that G is entire if A[G] is an integral domain, and strongly entire if A[G]/eA[G] is an integral domain. It is conjectured that G is (strongly) entire if and only if it has no finite orbits on X. In the absence of a proof of this conjecture, can one show the following:

If the permutation groups G1 on X1 and G2 on X2 are (strongly) entire, then G1 × G2 (in its intransitive action on X1 union X2) is (strongly) entire.

Q3) Find the truth value and from that information find the logically equivalent disjunctive normal form.

                 a. [(p  q)  r]                                                 b. P  (q  r)

Solution: a. (p  q  r) V (p  q  r) V (p  q  r)

                 b. (p  q  r) V (p  q  r) V (p  q  r) (circled false outputs)

Q4) Consider an algebraic system (G, *), where G is the set of all non-zero real numbers and * is a binary operation defined by

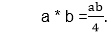
Show that (G, *) is an abelian group.

Solution:

Closure Property: The set G is closed under the operation *, since a * b = 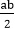 is a real number. Hence, it belongs to G.

Associative Property: The operation * is associative. Let a,b,c∈G, then we have

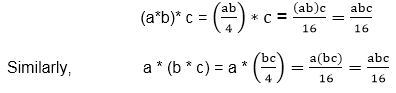
Identity: To find the identity element, let us assume that e is a +ve real number. Then e * a = a, where a ∈G.

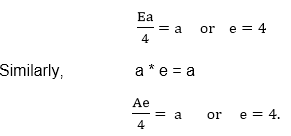
Thus, the identity element in G is 4.

Q5) Consider the lattice of all +ve integers I+ under the operation of divisibility. The lattice Dn of all divisors of n > 1 is a sub-lattice of I+.

Determine all the sub-lattices of D30 that contain at least four elements, D30={1,2,3,5,6,10,15,30}.

Solution: The sub-lattices of D30 that contain at least four elements are as follows:

1. {1, 2, 6, 30}          2. {1, 2, 3, 30}
3. {1, 5, 15, 30}          4. {1, 3, 6, 30}
5. {1, 5, 10, 30}          6. {1, 3, 15, 30}
7. {2, 6, 10, 30}

Q6) Write the dual of following Boolean expressions:

1. (x1*x2) + (x1*x3')         2. (1+x2)*( x1+1)
3. (a ∧(b∧c))

Solution:

1. ( x1+x2)*( x1+x3')         2. (0*x2)+( x1*0)
3. (a ∨(b∧c))

Q7) Simplify: AB(A + B)(B + B):

Q9)) Show that (2, 5) encoding function e B2 B5 defined by

e(00) = 01100e(10) = 10001

e (01) = 01110e(11) = 11011

Is a group code.