UNIT 1

Bessel function

1. Prove that 8 Jn’’(x)=Jn-3(x)-3Jn-1(x) + 3 Jn+1(x) – Jn+3(x)
2. Prove that Jn is an even function if n is a integer and is an odd function if n is odd integer
3. Obtain J6(x) in terms of J0(x) and J1(x)
4. Prove that J-1/2=. Cos x
5. Prove that J0’(x)=-J1(x)
6. Prove that 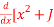3(2x)]=2x2J2(2x) – xJ3(2x)
7. Evaluate 3(x)dx and express the result in terms of J0 and J1
8. Prove that 0(x)dx=x.logx.J1(x)+J0(x)
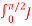9. Prove that 1(x cosθ) dθ =
10. Prove that J0’’(x)=-2J1(x)

1

UNIT 1

Bessel function

1. Prove that 8 Jn’’(x)=Jn-3(x)-3Jn-1(x) + 3 Jn+1(x) – Jn+3(x)
2. Prove that Jn is an even function if n is a integer and is an odd function if n is odd integer
3. Obtain J6(x) in terms of J0(x) and J1(x)
4. Prove that J-1/2=. Cos x
5. Prove that J0’(x)=-J1(x)
6. Prove that 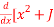3(2x)]=2x2J2(2x) – xJ3(2x)
7. Evaluate 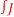3(x)dx and express the result in terms of J0 and J1
8. Prove that 0(x)dx=x.logx.J1(x)+J0(x)
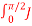9. Prove that 1(x cosθ) dθ =
10. Prove that J0’’(x)=-2J1(x)

1