Unit - 2
Relational query languages
Q. 1) Write the Armstrong’s axioms ?
Ans : Armstrong’s axioms
● The Axioms of Armstrong is a set of laws.
● It offers a basic reasoning technique for functional dependencies.
● It was created in 1974 by William W. Armstrong.
● It is used to infer on a relational database all of the functional dependencies.
Various Axioms Rules
A. Primary Rules
Rule 1 : Reflexivity
If A is a set of attributes and B is a subset of A, then A holds B.
Rule 2 : Augmentation
If A hold B and C is a set of attributes, then AC holds BC. {AC → BC}
It means that attribute in dependencies does not change the basic dependencies.
Rule 3 : Transitivity
If A holds B and B holds C, then A holds C.
If {A → B} and {B → C}, then {A → C}
A holds B {A → B} means that A functionally determines B.
B.Secondary Rules
Rule 1 : Union
If A holds B and A holds C, then A holds BC.
If{A → B} and {A → C}, then {A → BC}
Rule 2 : Decomposition
If A holds BC and A holds B, then A holds C.
If{A → BC} and {A → B}, then {A → C}
Rule 3 : Pseudo Transitivity
If A holds B and BC holds D, then AC holds D.
If{A → B} and {BC → D}, then {AC → D}
Trivial Functional Dependency
Trivial : If P holds Q (P → Q), where P is a subset of Q, then it is called a Trivial Functional Dependency. Trivial always holds Functional Dependency.
Non-Trivial : If P holds Q (P → Q), where Q is not a subset of P, then it is called as a Non-Trivial Functional Dependency.
Completely Non-Trivial : If P holds Q (P → Q), where P intersect Y = Φ, it is called as a Completely Non-Trivial Functional Dependency.
Q. 2) What is the normal forms ?
Ans : Normal forms
Normalization is often executed as a series of different forms. Each normal form has its own properties. As normalization proceeds, the relations become progressively more restricted in format, and also less vulnerable to update anomalies. For the relational data model, it is important to bring the relation only in first normal form (1NF) that is critical in creating relations. All the remaining forms are optional.
A relation R is said to be normalized if it does not create any anomaly for three basic operations: insert, delete and update
Fig : types of normal forms
- First Normal Form (1NF):
A relation r is in 1NF if and only if every tuple contains only atomic attributes means exactly one value for each attribute. As per the rule of first normal form, an attribute of a table cannot hold multiple values. It should hold only atomic values.
Example: suppose Company has created a employee table to store name, address and mobile number of employees.
Emp_id | Emp_name | Emp_address | Emp_mobile |
101 | Rachel | Mumbai | 9817312390 |
102 | John | Pune | 7812324252, 9890012244 |
103 | Kim | Chennai | 9878381212 |
104 | Mary | Bangalore | 9895000123, 7723455987 |
In the above table, two employees John, Mary has two mobile numbers. So, the attribute, emp_mobile is Multivalued attribute.
So, this table is not in 1NF as the rule says, “Each attribute of a table must have atomic values”. But in above table the the attribute, emp_mobile, is not atomic attribute as it contains multiple values. So, it violates the rule of 1 NF.
Following solution brings employee table in 1NF.
Emp_id | Emp_name | Emp_address | Emp_mobile |
101 | Rachel | Mumbai | 9817312390 |
102 | John | Pune | 7812324252 |
102 | John | Pune | 9890012244 |
103 | Kim | Chennai | 9878381212 |
104 | Mary | Bangalore | 9895000123 |
104 | Mary | Bangalore | 7723455987 |
- Second Normal Form (2NF)
A table is said to be in 2NF if both of the following conditions are satisfied:
● Table is in 1 NF.
● No non-prime attribute is dependent on the proper subset of any candidate key of table. It means non-prime attribute should fully functionally dependent on whole candidate key of a table. It should not depend on part of key.
An attribute that is not part of any candidate key is known as non-prime attribute.
Example: Suppose a school wants to store data of teachers and the subjects they teach. Since a teacher can teach more than one subjects, the table can have multiple rows for the same teacher.
Teacher_id | Subject | Teacher_age |
111 | DSF | 28 |
111 | DBMS | 28 |
222 | CNT | 35 |
333 | OOPL | 38 |
333 | FDS | 38 |
For above table:
Candidate Keys: {Teacher_Id, Subject}
Non prime attribute: Teacher_Age
The table is in 1 NF because each attribute has atomic values. However, it is not in 2NF because non-prime attribute Teacher_Age is dependent on Teacher_Id alone which is a proper subset of candidate key. This violates the rule for 2NF as the rule says “no non-prime attribute is dependent on the proper subset of any candidate key of the table”.
To bring above table in 2NF we can break it in two tables (Teacher_Detalis and
Teacher_Subject) like this:
Teacher_Details table:
Teacher_id | Teacher_age |
111 | 28 |
222 | 35 |
333 | 38 |
Teacher_Subject table:
Teacher_id | Subject |
111 | DSF |
111 | DBMS |
222 | CNT |
333 | OOPL |
333 | FDS |
Now these two tables are in 2NF.
- Third Normal Form (3NF)
A table design is said to be in 3NF if both the following conditions hold:
● Table must be in 2NF.
● Transitive functional dependency from the relation must be removed.
So it can be stated that, a table is in 3NF if it is in 2NF and for each functional dependency
P->Q at least one of the following conditions hold:
● P is a super key of table
● Q is a prime attribute of table
An attribute that is a part of one of the candidate keys is known as prime attribute.
Transitive functional dependency:
A functional dependency is said to be transitive if it is indirectly formed by two functional dependencies.
For example:
P->R is a transitive dependency if the following three functional dependencies hold true:
1) P->Q and
2) Q->R
Example: suppose a company wants to store information about employees. Then the table Employee_Details looks like this:
Emp_id | Emp_name | Manager_id | Mgr_Dept | Mgr_Name |
E1 | Hary | M1 | IT | William |
E2 | John | M1 | IT | William |
E3 | Nil | M2 | SALES | Stephen |
E4 | Mery | M3 | HR | Johnson |
E5 | Steve | M2 | SALSE | Stephen |
Super keys: {emp_id}, {emp_id, emp_name}, {emp_id, emp_name, Manager_id}
Candidate Key: {emp_id}
Non-prime attributes: All attributes except emp_id are non-prime as they are not subpart part of any candidate keys.
Here, Mgr_Dept, Mgr_Name dependent on Manager_id. And, Manager_id is dependent on emp_id that makes non-prime attributes (Mgr_Dept, Mgr_Name) transitively dependent on super key (emp_id). This violates the rule of 3NF.
To bring this table in 3NF we have to break into two tables to remove transitive dependency.
Employee_Details table:
Emp_id | Emp_name | Manager_id |
E1 | Hary | M1 |
E2 | John | M1 |
E3 | Nil | M2 |
E4 | Mery | M3 |
E5 | Steve | M2 |
Manager_Details table:
Manager_id | Mgr_Dept | Mgr_Name |
M1 | IT | William |
M2 | SALSE | Stephen |
M3 | HR | Johnson |
n advance version of 3NF. BCNF is stricter than 3NF. A table complies with BCNF if it is in 3NF and for every functional dependency X->Y, X should be the super key of the table.
Example: Suppose there is a company wherein employees work in more than one
Department. They store the data like this:
Emp_id | Emp_nationality | Emp_dept | Dept_type | Dept_no_of_emp |
101 | Indian | Planning | D01 | 100 |
101 | Indian | Accounting | D01 | 50 |
102 | Japanese | Technical support | D14 | 300 |
102 | Japanese | Sales | D14 | 100 |
Functional dependencies in the table above:
Emp_id ->emp_nationality
Emp_dept -> {dept_type, dept_no_of_emp}
Candidate key: {emp_id, emp_dept}
The table is not in BCNF as neither emp_id nor emp_dept alone are keys. To bring this table in BCNF we can break this table in three tables like:
Emp_nationality table:
Emp_id | Emp_nationality |
101 | Indian |
102 | Japanese |
Emp_dept table:
Emp_dept | Dept_type | Dept_no_of_emp |
Planning | D01 | 100 |
Accounting | D01 | 50 |
Technical support | D14 | 300 |
Sales | D14 | 100 |
Emp_dept_mapping table:
Emp_id | Emp_dept |
101 | Planning |
101 | Accounting |
102 | Technical support |
102 | Sales |
Functional dependencies:
Emp_id ->; emp_nationality
Emp_dept -> {dept_type, dept_no_of_emp}
Candidate keys:
For first table: emp_id
For second table: emp_dept
For third table: {emp_id, emp_dept}
This is now in BCNF as in both functional dependencies left side is a key.
- Fourth Normal Form (4NF)
A relation is in the 4NF if it is in BCNF and has no multi valued dependencies.
It means relation R is in 4NF if and only if whenever there exist subsets A and B of the
Attributes of R such that the Multi valued dependency AààB is satisfied then all attributes of R are also functionally dependent on A.
Multi-Valued Dependency
● The multi-valued dependency X -> Y holds in a relation R if whenever we have two tuples of R that agree (same) in all the attributes of X, then we can swap their Y components and get two new tuples that are also in R.
● Suppose a student can have more than one subject and more than one activity.
- Fifth Normal Form (5NF)
A table is in the 5NF if it is in 4NF and if for all Join dependency (JD) of (R1, R2, R3, ..., Rm) in R, every Ri is a super key for R. It means:
● A table is in the 5NF if it is in 4NF and if it cannot have a lossless decomposition in to any number of smaller tables (relations).
● It is also known as Project-join normal form (PJ/NF)
Example
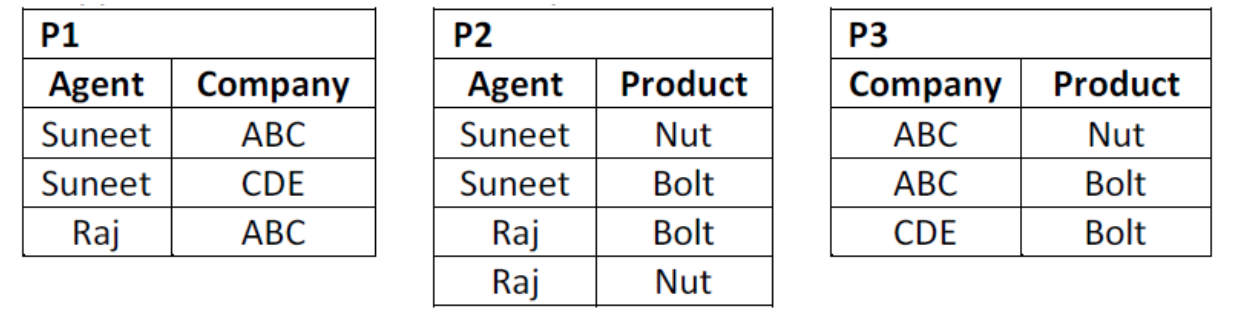
i. AGENT_COMPANY_PRODUCT (Agent, Company, Product)
Ii. This table lists agents, the companies they work for and the products they sell for those companies. ‘The agents do not necessarily sell all the products supplied by the companies they do business with.
An example of this table might be:
AGENT_COMPANY_PRODUCT | ||
Agent | Company | Product |
Suneet | ABC | Nut |
Raj | ABC | Bolt |
Raj | ABC | Nut |
Suneet | CDE | Bolt |
Suneet | ABC | Bolt |
1. The table is in 4NF because it contains no multi-valued dependency.
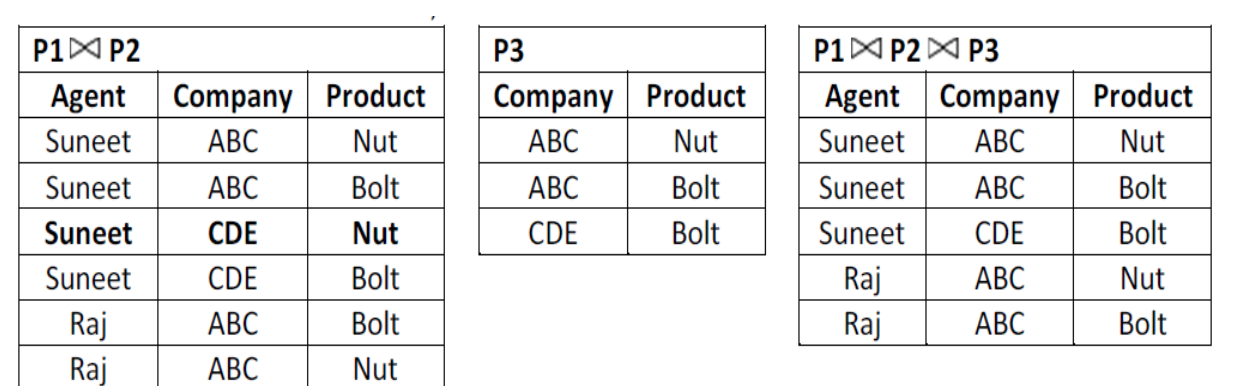
2. Suppose that the table is decomposed into its three relations, P1, P2 and P3.
i. But if we perform natural join between the above three relations then no spurious (extra) rows are added so this decomposition is called lossless decomposition.
Ii. So above three tables P1, P2 and P3 are in 5 NF
Q. 3) What is the join strategy ?
Ans : Join strategy
There are numerous joining techniques between two tables to perform. The distribution of data and columns chosen for joins greatly affects the implementation plan and the join strategy selected.
Broadly, there are four types of methods for joining:
● Nested Join
● Product Join
● Merge Join
● Hash Join
Nested join :
This join strategy uses 'special indexes' (be it a single primary index or a unique secondary index) from one of the join tables to retrieve a single record. The join condition should also fit a column from a single retrieved row to the second table's main /Secondary index. On the other table, a single row matches one or more rows .
Product join :
Product join compares every row in the second table from one table to every row, assuming the join condition as 1=1, and applies the filter to the result set if 'WHERE' determines some condition.
Example: If there are 20 rows in the 1st table and 10 records in the 2nd table, product join results in 200 (20X10) rows. In general, product interactions are triggered by errors
Popular triggers that can activate 'Product Join'
● The question defines neither the join condition nor the correct 'Where' clause.
● The condition of inequality is used as the joining condition
For product joining, there are 2 sub-strategies
- Big table Small table strategy:
When one table is very small, this technique comes into play. In this method, the small table will be duplicated into spools on all the AMPs. By scanning all-rows, the bigger table is then joined to the product spool.
2. General strategy:
All the rows from both tables are scanned and moved to different spools in this technique. Using a product joint, these spools will then be joined.
Merge Join:
For equi joins and exclusions as well, this is the most common join technique that comes into play.
For merge join, there are 5 sub-strategies
- PI-PI join : This method comes into play as the columns of both table columns are the key index of the respective tables. On local amps, rows will be directly joined (merge join) without transferring them to spool for joining.
2. PI- No PI Join : When joining columns of one table is the primary index, and joining columns of the second table is not the primary index, this technique comes into play.
On the relation columns, rows from the second table will be hashed and sorted by rowhash. To link with the 1st table, Rowhash is then sent to spool on the corresponding Amps. By scanning all-rows, the 1st table is then merged into a spool.
3. No PI - No PI join : When joining columns from both tables are not primary index columns, this technique comes into play. On the joining columns, rows from both tables are checked and hashed. For each table, Rowhash is then sorted and shifted to separate spools. Using a merge join, certain spools will be joined with each other.
4. Exclusion Join : When one table is used to remove data from another table, this technique comes into play. If 'NOT EXISTS' and 'NOT IN' are used, Exclusion Join is applicable.
5. Big table Small table strategy : When one table is very small, this technique comes into play. In this method, the small table will be duplicated into spools on all the AMPs. By scanning all-rows, the bigger table is then combined together into a spool.
Hash join :
This join approach is to join the merge family, but it performs much better than joining Merge Join & Product. When one table needs to be small enough to fit entirely in the memory, Hash join will be used.
There are 2 sub strategies for hash join
- Dynamic hash join : One table must be small enough to fit entirely into a single partition in the memory, and compared to another table, it should be very small. Dynamic hash join, without transferring large table to spool, offers the ability to join tables. Only when two tables are joined based on non-primary index columns will this work.
2. Classic / Partitioned hash join : When one table is too large for hash processing to fit into a single partition memory, the device splits the table into many smaller partitions that are small enough to fit into the memory available.
On both joining tables, hash join partitions are generated by hashing both table rows on their joining columns in such a way that rows from the hash join partition of one table can only fit rows in the hash join partition of the other table.
Q. 4) Define the term quer equivalence ?
Ans : Query equivalence
If both expressions generate the same set of records, all two relational expressions are said to be equal. We may use them interchangeably when two terms are identical. We can use any expression that provides better results, i.e.;
The equivalence rule states that expressions of two forms are the same or identical because in any legal database case, both expressions generate the same outputs. This implies that the expression of the first form may be replaced by that of the second form, and the expression of the second form may be replaced by the expression of the first form.
The query-evaluation plan optimizer therefore uses such an equivalence rule or process to turn expressions into logically equivalent ones.
For the transformation of relational expressions, the optimizer uses different equivalence principles for relational-algebra expressions. We will use the following symbols to define any rule:
θ, θ1, θ2 … : Used for the predicates being denoted.
L1, L2, L3 … : Used when denoting an attribute list.
E, E1, E2 …. : Represents the expressions of relational-algebra
Equivalence Rules
Rule 1: Cascade of σ
This rule notes the deconstruction into a series of individual selections of the conjunctive selection operations. Such a transition is referred to as a σ cascade.
σθ1 ᴧ θ 2 (E) = σθ1 (σθ2 (E))
Rule 2: Commutative Rule
Theta Join (θ) is commutative.
E1 ⋈ θ E 2 = E 2 ⋈ θ E 1
Rule 3: Cascade of ∏
This rule states that in the sequence of the projection operations, we only need the final operations, and other operations are omitted. A transformation of this kind is referred to as a cascade of ∏.
∏L1 (∏L2 (. . . (∏Ln (E)) . . . )) = ∏L1 (E)
Rule 4: The choices can be paired with Cartesian products and theta joins.
1. σθ (E1 x E2) = E1θ ⋈ E2
2. σθ1 (E1 ⋈ θ2 E2) = E1 ⋈ θ1ᴧθ2 E2
Rule 5: Associative Rule
This rule notes that associative operations are natural joining operations.
(E1 ⋈ E2) ⋈ E3 = E1 ⋈ (E2 ⋈ E3)
Rule 6: The union and intersection set operations are associative.
(E1 υ E2) υ E3 = E1 υ (E2 υ E3)
(E1 ꓵ E2) ꓵ E3 = E1 ꓵ (E2 ꓵ E3)
Q. 5) What is the lossless design ?
Ans : Lossless design
❏ If the data is not lost from the decomposing relationship, then the decomposition is lossless.
❏ The lossless decomposition ensures that the union of relationships can lead to the decomposition of the same relationship.
❏ If natural joins of all the decomposition give the original relation, the relationship is said to be lossless decomposition.
Now let's see an instance:
<EmpInfo>
Emp_ID | Emp_Name | Emp_Age | Emp_Location | Dept_ID | Dept_Name |
E101 | Jerry | 29 | Newyork | Dpt1 | Operations |
E102 | Henry | 32 | Newyork | Dpt2 | HR |
E103 | Tom | 22 | Texas | Dpt3 | Finance |
Decompose the table listed above into two tables:
<EmpDetails>
Emp_ID | Emp_Name | Emp_Age | Emp_Location |
E101 | Jerry | 29 | Newyork |
E102 | Henry | 32 | Newyork |
E103 | Tom | 22 | Texas |
<DeptDetails>
Dept_ID | Emp_ID | Dept_Name |
Dpt1 | E101 | Operations |
Dpt2 | E102 | HR |
Dpt3 | E103 | Finance |
Now, Natural Join is added to the two tables above,
The outcome will be −
EmpDetails ⋈ DeptDetails
Emp_ID | Emp_Name | Emp_Age | Emp_Location | Dept_ID | Dept_Name |
E101 | Jerry | 29 | Newyork | Dpt1 | Operations |
E102 | Henry | 32 | Newyork | Dpt2 | HR |
E103 | Tom | 22 | Texas | Dpt3 | Finance |
Therefore, the above relationship had decomposition without loss, i.e. no data loss.
Q. 6) What do you mean by Dependency preservation ?
Ans : Dependency preservation
❏ It is an integral restriction of the database.
❏ In the preservation of dependency, each dependency must satisfy at least one decomposed table.
❏ If the R-relationship is broken down into the R-relationship R1 and R2, then the R-relationship must either be part of R1 or R2, or it must be derived from the combination of the R1 and R2 functional dependencies.
❏ Suppose, for example, that there is a relation between R (A, B, C, D) and the set of functional dependencies (A->BC). Relational R is broken down into R1(ABC) and R2(AD), which maintains dependence since FD A->BC is part of the R1 relationship (ABC).
Decomposition D = { R1, R2, R3,,..,, Rm} of R is said to maintain dependence with respect to F if the union of F's projections on each Ri is equal to F. In D. R-join of R1, R1 over X, in other words. The dependencies are retained since each dependency in F represents a database constraint. If decomposition is not dependency-preserving, the decomposition loses any dependency.
Example :
Let R(A,B,C,D) be a relationship and set the FDs to F={ A -> B, A -> C, C -> D}.
Relationship R is broken down into —
R1 = (A, B, C) with FDs F1 = {A -> B, A -> C}, and
R2 = (C, D) with FDs F2 = {C -> D}.
F' = F1 ∪ F2 = {A -> B, A -> C, C -> D}
so, F' = F.
And so, F'+ = F+.
Thus, the decomposition is dependency preserving .
Q. 7) Define the term SQL3 ?
Ans : SQL3
Basically, SQL3 contains Object-Oriented dbms, OO-dbms data description and management techniques, while retaining the platform of relational dbms. DBMSs that support SQL3 are called Object-Relational or or-dbms 'based on this merger of concepts and techniques.
With these extensions, the latest version of SQL in development is also referred to as "SQL3". SQL3 object facilities mainly include extensions to SQL type facilities, but extensions to SQL table facilities may also be considered important. Additional facilities provide control structures for building, maintaining, and querying persistent object-like data structures to render SQL a computer-complete language.
The added equipment is intended to be compliant with the existing SQL92 specification upwards. This and other parts of the SQL3 Features Matrix focus mainly on the SQL3 extensions applicable to the modelling of artefacts.
In SQL, however, several other changes have also been made [Mat96]. Furthermore, it should be noted that SQL3 continues to be developed, so the definition of SQL3 in this Features Matrix does not necessarily reflect the final language requirements that have been accepted.
The parts of SQL3 that provide the primary basis for object-oriented structures to be supported are:
● Types that are user-defined (ADTs, named row types, and distinct types)
● For row types and reference types, type constructors
● For collection types, category constructors (sets, lists, and multi sets)
● Functions and procedures that are user-defined
● Assistance for big items (BLOBs and CLOBs)
Used of SQL
For interacting with a database, SQL is used. It is the basic language for relational database management systems, according to ANSI (American National Standards Institute). SQL statements are used for performing tasks, such as modifying database data or extracting database data.
Q. 8) Write short notes on MYSQL ?
Ans : MYSQL
MySQL is a relational database management system that runs on many platforms and is open-source. To support several storage engines, it provides multi-user access and is backed by Oracle.
MySQL is a fast and easy-to-use RDBMS that is used for the production of various small and large-scale applications. Various applications such as Joomla, WordPress, Drupal and many more are commonly used.
Under the terms of the GNU General Public License, as well as under a range of proprietary agreements, the source code of MySQL OpenSources is accessible. Several paid versions are available for proprietary use that provide additional functionalities. MySQL was originally developed by MySQL AB, which is now owned by Oracle Corporation, a Swedish company.
MySQL Server Software Version is available in various versions, such as Commercial Edition and Community Editions, etc., which are listed below:
- MySQL Community Edition
- MySQL Commercial Edition
- MySQL Enterprise Edition
- MySQL Standard Edition
- MySQL Classic Edition
- MySQL Cluster CGE
Features of MYSQL open sources :
- Platform Independent
- Replication
- Relational Database System
- Client/Server Architecture
- Query Language
- Easy to Use
Q. 9) What is DDl and write their commands ?
Ans : DDL
In reality, the DDL or Data Description Language consists of SQL commands that can be used to define the schema for the database. It basically deals with database schema definitions and is used to construct and change the configuration of database objects in the database.
Some of the commands that fall under DDL are as follows:
● CREATE
● ALTER
● DROP
● TRUNCATE
CREATE
It is used in the database for the development of a new table
Syntax
CREATE TABLE TABLE_NAME (COLUMN_NAME DATATYPES[,....]);
Example
CREATE TABLE STUDENT(Name VARCHAR2(20), Address VARCHAR2(100), DOB DATE);
ALTER
It is used to modify the database structure. This move may be either to change the characteristics of an existing attribute or to add a new attribute, likely.
Syntax
In order to add a new column to the table:
ALTER TABLE table_name ADD column_name COLUMN-definition;
To change the current table column:
ALTER TABLE MODIFY(COLUMN DEFINITION....);
Example
ALTER TABLE STU_DETAILS ADD(ADDRESS VARCHAR2(20));
ALTER TABLE STU_DETAILS MODIFY (NAME VARCHAR2(20));
Drop
It is used to delete both the structure of the table and the record.
Syntax
DROP TABLE ;
Example
DROP TABLE STUDENT;
TRUNCATE
It is used to erase from the table all rows and free up the space containing the table.
Syntax
TRUNCATE TABLE table_name;
Example
TRUNCATE TABLE STUDENT;
Q. 10) What is the DML and write their commands ?
Ans : DML
To change the database, DML commands are used. It is responsible for all forms of database changes.
The DML command is not auto-committed, which means all the changes in the database will not be permanently saved. There may be rollbacks.
Commands under DML
- SELECT
The Select Statement retrieves data from the database as defined by the constraints.
Select command with some clauses :
SELECT <COLUMN NAME>
FROM <TABLE NAME>
WHERE <CONDITION>
GROUP BY <COLUMN LIST>
HAVING <CRITERIA FOR FUNCTION RESULTS>
ORDER BY <COLUMN LIST>
Syntax
SELECT * FROM <table_name>;
Example
SELECT * FROM student;
OR
SELECT * FROM student
Where age >=15 ;
b. INSERT
The INSERT statement is a query from SQL. It is used for the insertion of data into a table row.
Syntax
INSERT INTO TABLE_NAME
(col1, col2, col3,.... Col N)
VALUES (value1, value2, value3, .... ValueN);
Or
INSERT INTO TABLE_NAME
VALUES (value1, value2, value3, .... ValueN);
c. UPDATE
This command is used to update or alter the value of a table column.
Syntax
UPDATE table_name SET [column_name1= value1,...column_nameN = valueN] [WHERE CONDITION]
d. DELETE
It is used to extract a table from one or more rows.
Syntax
DELETE FROM table_name [WHERE condition];
Unit - 2
Relational query languages
Q. 1) Write the Armstrong’s axioms ?
Ans : Armstrong’s axioms
● The Axioms of Armstrong is a set of laws.
● It offers a basic reasoning technique for functional dependencies.
● It was created in 1974 by William W. Armstrong.
● It is used to infer on a relational database all of the functional dependencies.
Various Axioms Rules
A. Primary Rules
Rule 1 : Reflexivity
If A is a set of attributes and B is a subset of A, then A holds B.
Rule 2 : Augmentation
If A hold B and C is a set of attributes, then AC holds BC. {AC → BC}
It means that attribute in dependencies does not change the basic dependencies.
Rule 3 : Transitivity
If A holds B and B holds C, then A holds C.
If {A → B} and {B → C}, then {A → C}
A holds B {A → B} means that A functionally determines B.
B.Secondary Rules
Rule 1 : Union
If A holds B and A holds C, then A holds BC.
If{A → B} and {A → C}, then {A → BC}
Rule 2 : Decomposition
If A holds BC and A holds B, then A holds C.
If{A → BC} and {A → B}, then {A → C}
Rule 3 : Pseudo Transitivity
If A holds B and BC holds D, then AC holds D.
If{A → B} and {BC → D}, then {AC → D}
Trivial Functional Dependency
Trivial : If P holds Q (P → Q), where P is a subset of Q, then it is called a Trivial Functional Dependency. Trivial always holds Functional Dependency.
Non-Trivial : If P holds Q (P → Q), where Q is not a subset of P, then it is called as a Non-Trivial Functional Dependency.
Completely Non-Trivial : If P holds Q (P → Q), where P intersect Y = Φ, it is called as a Completely Non-Trivial Functional Dependency.
Q. 2) What is the normal forms ?
Ans : Normal forms
Normalization is often executed as a series of different forms. Each normal form has its own properties. As normalization proceeds, the relations become progressively more restricted in format, and also less vulnerable to update anomalies. For the relational data model, it is important to bring the relation only in first normal form (1NF) that is critical in creating relations. All the remaining forms are optional.
A relation R is said to be normalized if it does not create any anomaly for three basic operations: insert, delete and update
Fig : types of normal forms
- First Normal Form (1NF):
A relation r is in 1NF if and only if every tuple contains only atomic attributes means exactly one value for each attribute. As per the rule of first normal form, an attribute of a table cannot hold multiple values. It should hold only atomic values.
Example: suppose Company has created a employee table to store name, address and mobile number of employees.
Emp_id | Emp_name | Emp_address | Emp_mobile |
101 | Rachel | Mumbai | 9817312390 |
102 | John | Pune | 7812324252, 9890012244 |
103 | Kim | Chennai | 9878381212 |
104 | Mary | Bangalore | 9895000123, 7723455987 |
In the above table, two employees John, Mary has two mobile numbers. So, the attribute, emp_mobile is Multivalued attribute.
So, this table is not in 1NF as the rule says, “Each attribute of a table must have atomic values”. But in above table the the attribute, emp_mobile, is not atomic attribute as it contains multiple values. So, it violates the rule of 1 NF.
Following solution brings employee table in 1NF.
Emp_id | Emp_name | Emp_address | Emp_mobile |
101 | Rachel | Mumbai | 9817312390 |
102 | John | Pune | 7812324252 |
102 | John | Pune | 9890012244 |
103 | Kim | Chennai | 9878381212 |
104 | Mary | Bangalore | 9895000123 |
104 | Mary | Bangalore | 7723455987 |
- Second Normal Form (2NF)
A table is said to be in 2NF if both of the following conditions are satisfied:
● Table is in 1 NF.
● No non-prime attribute is dependent on the proper subset of any candidate key of table. It means non-prime attribute should fully functionally dependent on whole candidate key of a table. It should not depend on part of key.
An attribute that is not part of any candidate key is known as non-prime attribute.
Example: Suppose a school wants to store data of teachers and the subjects they teach. Since a teacher can teach more than one subjects, the table can have multiple rows for the same teacher.
Teacher_id | Subject | Teacher_age |
111 | DSF | 28 |
111 | DBMS | 28 |
222 | CNT | 35 |
333 | OOPL | 38 |
333 | FDS | 38 |
For above table:
Candidate Keys: {Teacher_Id, Subject}
Non prime attribute: Teacher_Age
The table is in 1 NF because each attribute has atomic values. However, it is not in 2NF because non-prime attribute Teacher_Age is dependent on Teacher_Id alone which is a proper subset of candidate key. This violates the rule for 2NF as the rule says “no non-prime attribute is dependent on the proper subset of any candidate key of the table”.
To bring above table in 2NF we can break it in two tables (Teacher_Detalis and
Teacher_Subject) like this:
Teacher_Details table:
Teacher_id | Teacher_age |
111 | 28 |
222 | 35 |
333 | 38 |
Teacher_Subject table:
Teacher_id | Subject |
111 | DSF |
111 | DBMS |
222 | CNT |
333 | OOPL |
333 | FDS |
Now these two tables are in 2NF.
- Third Normal Form (3NF)
A table design is said to be in 3NF if both the following conditions hold:
● Table must be in 2NF.
● Transitive functional dependency from the relation must be removed.
So it can be stated that, a table is in 3NF if it is in 2NF and for each functional dependency
P->Q at least one of the following conditions hold:
● P is a super key of table
● Q is a prime attribute of table
An attribute that is a part of one of the candidate keys is known as prime attribute.
Transitive functional dependency:
A functional dependency is said to be transitive if it is indirectly formed by two functional dependencies.
For example:
P->R is a transitive dependency if the following three functional dependencies hold true:
1) P->Q and
2) Q->R
Example: suppose a company wants to store information about employees. Then the table Employee_Details looks like this:
Emp_id | Emp_name | Manager_id | Mgr_Dept | Mgr_Name |
E1 | Hary | M1 | IT | William |
E2 | John | M1 | IT | William |
E3 | Nil | M2 | SALES | Stephen |
E4 | Mery | M3 | HR | Johnson |
E5 | Steve | M2 | SALSE | Stephen |
Super keys: {emp_id}, {emp_id, emp_name}, {emp_id, emp_name, Manager_id}
Candidate Key: {emp_id}
Non-prime attributes: All attributes except emp_id are non-prime as they are not subpart part of any candidate keys.
Here, Mgr_Dept, Mgr_Name dependent on Manager_id. And, Manager_id is dependent on emp_id that makes non-prime attributes (Mgr_Dept, Mgr_Name) transitively dependent on super key (emp_id). This violates the rule of 3NF.
To bring this table in 3NF we have to break into two tables to remove transitive dependency.
Employee_Details table:
Emp_id | Emp_name | Manager_id |
E1 | Hary | M1 |
E2 | John | M1 |
E3 | Nil | M2 |
E4 | Mery | M3 |
E5 | Steve | M2 |
Manager_Details table:
Manager_id | Mgr_Dept | Mgr_Name |
M1 | IT | William |
M2 | SALSE | Stephen |
M3 | HR | Johnson |
n advance version of 3NF. BCNF is stricter than 3NF. A table complies with BCNF if it is in 3NF and for every functional dependency X->Y, X should be the super key of the table.
Example: Suppose there is a company wherein employees work in more than one
Department. They store the data like this:
Emp_id | Emp_nationality | Emp_dept | Dept_type | Dept_no_of_emp |
101 | Indian | Planning | D01 | 100 |
101 | Indian | Accounting | D01 | 50 |
102 | Japanese | Technical support | D14 | 300 |
102 | Japanese | Sales | D14 | 100 |
Functional dependencies in the table above:
Emp_id ->emp_nationality
Emp_dept -> {dept_type, dept_no_of_emp}
Candidate key: {emp_id, emp_dept}
The table is not in BCNF as neither emp_id nor emp_dept alone are keys. To bring this table in BCNF we can break this table in three tables like:
Emp_nationality table:
Emp_id | Emp_nationality |
101 | Indian |
102 | Japanese |
Emp_dept table:
Emp_dept | Dept_type | Dept_no_of_emp |
Planning | D01 | 100 |
Accounting | D01 | 50 |
Technical support | D14 | 300 |
Sales | D14 | 100 |
Emp_dept_mapping table:
Emp_id | Emp_dept |
101 | Planning |
101 | Accounting |
102 | Technical support |
102 | Sales |
Functional dependencies:
Emp_id ->; emp_nationality
Emp_dept -> {dept_type, dept_no_of_emp}
Candidate keys:
For first table: emp_id
For second table: emp_dept
For third table: {emp_id, emp_dept}
This is now in BCNF as in both functional dependencies left side is a key.
- Fourth Normal Form (4NF)
A relation is in the 4NF if it is in BCNF and has no multi valued dependencies.
It means relation R is in 4NF if and only if whenever there exist subsets A and B of the
Attributes of R such that the Multi valued dependency AààB is satisfied then all attributes of R are also functionally dependent on A.
Multi-Valued Dependency
● The multi-valued dependency X -> Y holds in a relation R if whenever we have two tuples of R that agree (same) in all the attributes of X, then we can swap their Y components and get two new tuples that are also in R.
● Suppose a student can have more than one subject and more than one activity.
- Fifth Normal Form (5NF)
A table is in the 5NF if it is in 4NF and if for all Join dependency (JD) of (R1, R2, R3, ..., Rm) in R, every Ri is a super key for R. It means:
● A table is in the 5NF if it is in 4NF and if it cannot have a lossless decomposition in to any number of smaller tables (relations).
● It is also known as Project-join normal form (PJ/NF)
Example
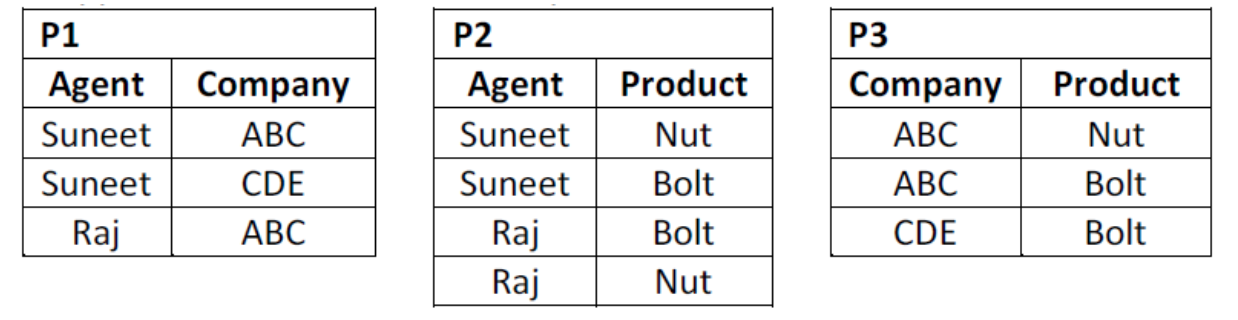
i. AGENT_COMPANY_PRODUCT (Agent, Company, Product)
Ii. This table lists agents, the companies they work for and the products they sell for those companies. ‘The agents do not necessarily sell all the products supplied by the companies they do business with.
An example of this table might be:
AGENT_COMPANY_PRODUCT | ||
Agent | Company | Product |
Suneet | ABC | Nut |
Raj | ABC | Bolt |
Raj | ABC | Nut |
Suneet | CDE | Bolt |
Suneet | ABC | Bolt |
1. The table is in 4NF because it contains no multi-valued dependency.
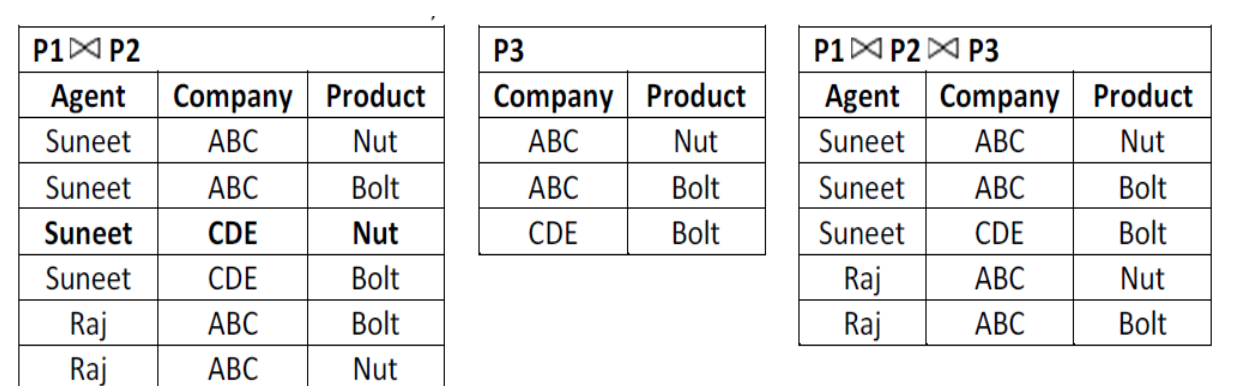
2. Suppose that the table is decomposed into its three relations, P1, P2 and P3.
i. But if we perform natural join between the above three relations then no spurious (extra) rows are added so this decomposition is called lossless decomposition.
Ii. So above three tables P1, P2 and P3 are in 5 NF
Q. 3) What is the join strategy ?
Ans : Join strategy
There are numerous joining techniques between two tables to perform. The distribution of data and columns chosen for joins greatly affects the implementation plan and the join strategy selected.
Broadly, there are four types of methods for joining:
● Nested Join
● Product Join
● Merge Join
● Hash Join
Nested join :
This join strategy uses 'special indexes' (be it a single primary index or a unique secondary index) from one of the join tables to retrieve a single record. The join condition should also fit a column from a single retrieved row to the second table's main /Secondary index. On the other table, a single row matches one or more rows .
Product join :
Product join compares every row in the second table from one table to every row, assuming the join condition as 1=1, and applies the filter to the result set if 'WHERE' determines some condition.
Example: If there are 20 rows in the 1st table and 10 records in the 2nd table, product join results in 200 (20X10) rows. In general, product interactions are triggered by errors
Popular triggers that can activate 'Product Join'
● The question defines neither the join condition nor the correct 'Where' clause.
● The condition of inequality is used as the joining condition
For product joining, there are 2 sub-strategies
- Big table Small table strategy:
When one table is very small, this technique comes into play. In this method, the small table will be duplicated into spools on all the AMPs. By scanning all-rows, the bigger table is then joined to the product spool.
2. General strategy:
All the rows from both tables are scanned and moved to different spools in this technique. Using a product joint, these spools will then be joined.
Merge Join:
For equi joins and exclusions as well, this is the most common join technique that comes into play.
For merge join, there are 5 sub-strategies
- PI-PI join : This method comes into play as the columns of both table columns are the key index of the respective tables. On local amps, rows will be directly joined (merge join) without transferring them to spool for joining.
2. PI- No PI Join : When joining columns of one table is the primary index, and joining columns of the second table is not the primary index, this technique comes into play.
On the relation columns, rows from the second table will be hashed and sorted by rowhash. To link with the 1st table, Rowhash is then sent to spool on the corresponding Amps. By scanning all-rows, the 1st table is then merged into a spool.
3. No PI - No PI join : When joining columns from both tables are not primary index columns, this technique comes into play. On the joining columns, rows from both tables are checked and hashed. For each table, Rowhash is then sorted and shifted to separate spools. Using a merge join, certain spools will be joined with each other.
4. Exclusion Join : When one table is used to remove data from another table, this technique comes into play. If 'NOT EXISTS' and 'NOT IN' are used, Exclusion Join is applicable.
5. Big table Small table strategy : When one table is very small, this technique comes into play. In this method, the small table will be duplicated into spools on all the AMPs. By scanning all-rows, the bigger table is then combined together into a spool.
Hash join :
This join approach is to join the merge family, but it performs much better than joining Merge Join & Product. When one table needs to be small enough to fit entirely in the memory, Hash join will be used.
There are 2 sub strategies for hash join
- Dynamic hash join : One table must be small enough to fit entirely into a single partition in the memory, and compared to another table, it should be very small. Dynamic hash join, without transferring large table to spool, offers the ability to join tables. Only when two tables are joined based on non-primary index columns will this work.
2. Classic / Partitioned hash join : When one table is too large for hash processing to fit into a single partition memory, the device splits the table into many smaller partitions that are small enough to fit into the memory available.
On both joining tables, hash join partitions are generated by hashing both table rows on their joining columns in such a way that rows from the hash join partition of one table can only fit rows in the hash join partition of the other table.
Q. 4) Define the term quer equivalence ?
Ans : Query equivalence
If both expressions generate the same set of records, all two relational expressions are said to be equal. We may use them interchangeably when two terms are identical. We can use any expression that provides better results, i.e.;
The equivalence rule states that expressions of two forms are the same or identical because in any legal database case, both expressions generate the same outputs. This implies that the expression of the first form may be replaced by that of the second form, and the expression of the second form may be replaced by the expression of the first form.
The query-evaluation plan optimizer therefore uses such an equivalence rule or process to turn expressions into logically equivalent ones.
For the transformation of relational expressions, the optimizer uses different equivalence principles for relational-algebra expressions. We will use the following symbols to define any rule:
θ, θ1, θ2 … : Used for the predicates being denoted.
L1, L2, L3 … : Used when denoting an attribute list.
E, E1, E2 …. : Represents the expressions of relational-algebra
Equivalence Rules
Rule 1: Cascade of σ
This rule notes the deconstruction into a series of individual selections of the conjunctive selection operations. Such a transition is referred to as a σ cascade.
σθ1 ᴧ θ 2 (E) = σθ1 (σθ2 (E))
Rule 2: Commutative Rule
Theta Join (θ) is commutative.
E1 ⋈ θ E 2 = E 2 ⋈ θ E 1
Rule 3: Cascade of ∏
This rule states that in the sequence of the projection operations, we only need the final operations, and other operations are omitted. A transformation of this kind is referred to as a cascade of ∏.
∏L1 (∏L2 (. . . (∏Ln (E)) . . . )) = ∏L1 (E)
Rule 4: The choices can be paired with Cartesian products and theta joins.
1. σθ (E1 x E2) = E1θ ⋈ E2
2. σθ1 (E1 ⋈ θ2 E2) = E1 ⋈ θ1ᴧθ2 E2
Rule 5: Associative Rule
This rule notes that associative operations are natural joining operations.
(E1 ⋈ E2) ⋈ E3 = E1 ⋈ (E2 ⋈ E3)
Rule 6: The union and intersection set operations are associative.
(E1 υ E2) υ E3 = E1 υ (E2 υ E3)
(E1 ꓵ E2) ꓵ E3 = E1 ꓵ (E2 ꓵ E3)
Q. 5) What is the lossless design ?
Ans : Lossless design
❏ If the data is not lost from the decomposing relationship, then the decomposition is lossless.
❏ The lossless decomposition ensures that the union of relationships can lead to the decomposition of the same relationship.
❏ If natural joins of all the decomposition give the original relation, the relationship is said to be lossless decomposition.
Now let's see an instance:
<EmpInfo>
Emp_ID | Emp_Name | Emp_Age | Emp_Location | Dept_ID | Dept_Name |
E101 | Jerry | 29 | Newyork | Dpt1 | Operations |
E102 | Henry | 32 | Newyork | Dpt2 | HR |
E103 | Tom | 22 | Texas | Dpt3 | Finance |
Decompose the table listed above into two tables:
<EmpDetails>
Emp_ID | Emp_Name | Emp_Age | Emp_Location |
E101 | Jerry | 29 | Newyork |
E102 | Henry | 32 | Newyork |
E103 | Tom | 22 | Texas |
<DeptDetails>
Dept_ID | Emp_ID | Dept_Name |
Dpt1 | E101 | Operations |
Dpt2 | E102 | HR |
Dpt3 | E103 | Finance |
Now, Natural Join is added to the two tables above,
The outcome will be −
EmpDetails ⋈ DeptDetails
Emp_ID | Emp_Name | Emp_Age | Emp_Location | Dept_ID | Dept_Name |
E101 | Jerry | 29 | Newyork | Dpt1 | Operations |
E102 | Henry | 32 | Newyork | Dpt2 | HR |
E103 | Tom | 22 | Texas | Dpt3 | Finance |
Therefore, the above relationship had decomposition without loss, i.e. no data loss.
Q. 6) What do you mean by Dependency preservation ?
Ans : Dependency preservation
❏ It is an integral restriction of the database.
❏ In the preservation of dependency, each dependency must satisfy at least one decomposed table.
❏ If the R-relationship is broken down into the R-relationship R1 and R2, then the R-relationship must either be part of R1 or R2, or it must be derived from the combination of the R1 and R2 functional dependencies.
❏ Suppose, for example, that there is a relation between R (A, B, C, D) and the set of functional dependencies (A->BC). Relational R is broken down into R1(ABC) and R2(AD), which maintains dependence since FD A->BC is part of the R1 relationship (ABC).
Decomposition D = { R1, R2, R3,,..,, Rm} of R is said to maintain dependence with respect to F if the union of F's projections on each Ri is equal to F. In D. R-join of R1, R1 over X, in other words. The dependencies are retained since each dependency in F represents a database constraint. If decomposition is not dependency-preserving, the decomposition loses any dependency.
Example :
Let R(A,B,C,D) be a relationship and set the FDs to F={ A -> B, A -> C, C -> D}.
Relationship R is broken down into —
R1 = (A, B, C) with FDs F1 = {A -> B, A -> C}, and
R2 = (C, D) with FDs F2 = {C -> D}.
F' = F1 ∪ F2 = {A -> B, A -> C, C -> D}
so, F' = F.
And so, F'+ = F+.
Thus, the decomposition is dependency preserving .
Q. 7) Define the term SQL3 ?
Ans : SQL3
Basically, SQL3 contains Object-Oriented dbms, OO-dbms data description and management techniques, while retaining the platform of relational dbms. DBMSs that support SQL3 are called Object-Relational or or-dbms 'based on this merger of concepts and techniques.
With these extensions, the latest version of SQL in development is also referred to as "SQL3". SQL3 object facilities mainly include extensions to SQL type facilities, but extensions to SQL table facilities may also be considered important. Additional facilities provide control structures for building, maintaining, and querying persistent object-like data structures to render SQL a computer-complete language.
The added equipment is intended to be compliant with the existing SQL92 specification upwards. This and other parts of the SQL3 Features Matrix focus mainly on the SQL3 extensions applicable to the modelling of artefacts.
In SQL, however, several other changes have also been made [Mat96]. Furthermore, it should be noted that SQL3 continues to be developed, so the definition of SQL3 in this Features Matrix does not necessarily reflect the final language requirements that have been accepted.
The parts of SQL3 that provide the primary basis for object-oriented structures to be supported are:
● Types that are user-defined (ADTs, named row types, and distinct types)
● For row types and reference types, type constructors
● For collection types, category constructors (sets, lists, and multi sets)
● Functions and procedures that are user-defined
● Assistance for big items (BLOBs and CLOBs)
Used of SQL
For interacting with a database, SQL is used. It is the basic language for relational database management systems, according to ANSI (American National Standards Institute). SQL statements are used for performing tasks, such as modifying database data or extracting database data.
Q. 8) Write short notes on MYSQL ?
Ans : MYSQL
MySQL is a relational database management system that runs on many platforms and is open-source. To support several storage engines, it provides multi-user access and is backed by Oracle.
MySQL is a fast and easy-to-use RDBMS that is used for the production of various small and large-scale applications. Various applications such as Joomla, WordPress, Drupal and many more are commonly used.
Under the terms of the GNU General Public License, as well as under a range of proprietary agreements, the source code of MySQL OpenSources is accessible. Several paid versions are available for proprietary use that provide additional functionalities. MySQL was originally developed by MySQL AB, which is now owned by Oracle Corporation, a Swedish company.
MySQL Server Software Version is available in various versions, such as Commercial Edition and Community Editions, etc., which are listed below:
- MySQL Community Edition
- MySQL Commercial Edition
- MySQL Enterprise Edition
- MySQL Standard Edition
- MySQL Classic Edition
- MySQL Cluster CGE
Features of MYSQL open sources :
- Platform Independent
- Replication
- Relational Database System
- Client/Server Architecture
- Query Language
- Easy to Use
Q. 9) What is DDl and write their commands ?
Ans : DDL
In reality, the DDL or Data Description Language consists of SQL commands that can be used to define the schema for the database. It basically deals with database schema definitions and is used to construct and change the configuration of database objects in the database.
Some of the commands that fall under DDL are as follows:
● CREATE
● ALTER
● DROP
● TRUNCATE
CREATE
It is used in the database for the development of a new table
Syntax
CREATE TABLE TABLE_NAME (COLUMN_NAME DATATYPES[,....]);
Example
CREATE TABLE STUDENT(Name VARCHAR2(20), Address VARCHAR2(100), DOB DATE);
ALTER
It is used to modify the database structure. This move may be either to change the characteristics of an existing attribute or to add a new attribute, likely.
Syntax
In order to add a new column to the table:
ALTER TABLE table_name ADD column_name COLUMN-definition;
To change the current table column:
ALTER TABLE MODIFY(COLUMN DEFINITION....);
Example
ALTER TABLE STU_DETAILS ADD(ADDRESS VARCHAR2(20));
ALTER TABLE STU_DETAILS MODIFY (NAME VARCHAR2(20));
Drop
It is used to delete both the structure of the table and the record.
Syntax
DROP TABLE ;
Example
DROP TABLE STUDENT;
TRUNCATE
It is used to erase from the table all rows and free up the space containing the table.
Syntax
TRUNCATE TABLE table_name;
Example
TRUNCATE TABLE STUDENT;
Q. 10) What is the DML and write their commands ?
Ans : DML
To change the database, DML commands are used. It is responsible for all forms of database changes.
The DML command is not auto-committed, which means all the changes in the database will not be permanently saved. There may be rollbacks.
Commands under DML
- SELECT
The Select Statement retrieves data from the database as defined by the constraints.
Select command with some clauses :
SELECT <COLUMN NAME>
FROM <TABLE NAME>
WHERE <CONDITION>
GROUP BY <COLUMN LIST>
HAVING <CRITERIA FOR FUNCTION RESULTS>
ORDER BY <COLUMN LIST>
Syntax
SELECT * FROM <table_name>;
Example
SELECT * FROM student;
OR
SELECT * FROM student
Where age >=15 ;
b. INSERT
The INSERT statement is a query from SQL. It is used for the insertion of data into a table row.
Syntax
INSERT INTO TABLE_NAME
(col1, col2, col3,.... Col N)
VALUES (value1, value2, value3, .... ValueN);
Or
INSERT INTO TABLE_NAME
VALUES (value1, value2, value3, .... ValueN);
c. UPDATE
This command is used to update or alter the value of a table column.
Syntax
UPDATE table_name SET [column_name1= value1,...column_nameN = valueN] [WHERE CONDITION]
d. DELETE
It is used to extract a table from one or more rows.
Syntax
DELETE FROM table_name [WHERE condition];
Unit - 2
Relational query languages
Q. 1) Write the Armstrong’s axioms ?
Ans : Armstrong’s axioms
● The Axioms of Armstrong is a set of laws.
● It offers a basic reasoning technique for functional dependencies.
● It was created in 1974 by William W. Armstrong.
● It is used to infer on a relational database all of the functional dependencies.
Various Axioms Rules
A. Primary Rules
Rule 1 : Reflexivity
If A is a set of attributes and B is a subset of A, then A holds B.
Rule 2 : Augmentation
If A hold B and C is a set of attributes, then AC holds BC. {AC → BC}
It means that attribute in dependencies does not change the basic dependencies.
Rule 3 : Transitivity
If A holds B and B holds C, then A holds C.
If {A → B} and {B → C}, then {A → C}
A holds B {A → B} means that A functionally determines B.
B.Secondary Rules
Rule 1 : Union
If A holds B and A holds C, then A holds BC.
If{A → B} and {A → C}, then {A → BC}
Rule 2 : Decomposition
If A holds BC and A holds B, then A holds C.
If{A → BC} and {A → B}, then {A → C}
Rule 3 : Pseudo Transitivity
If A holds B and BC holds D, then AC holds D.
If{A → B} and {BC → D}, then {AC → D}
Trivial Functional Dependency
Trivial : If P holds Q (P → Q), where P is a subset of Q, then it is called a Trivial Functional Dependency. Trivial always holds Functional Dependency.
Non-Trivial : If P holds Q (P → Q), where Q is not a subset of P, then it is called as a Non-Trivial Functional Dependency.
Completely Non-Trivial : If P holds Q (P → Q), where P intersect Y = Φ, it is called as a Completely Non-Trivial Functional Dependency.
Q. 2) What is the normal forms ?
Ans : Normal forms
Normalization is often executed as a series of different forms. Each normal form has its own properties. As normalization proceeds, the relations become progressively more restricted in format, and also less vulnerable to update anomalies. For the relational data model, it is important to bring the relation only in first normal form (1NF) that is critical in creating relations. All the remaining forms are optional.
A relation R is said to be normalized if it does not create any anomaly for three basic operations: insert, delete and update
Fig : types of normal forms
- First Normal Form (1NF):
A relation r is in 1NF if and only if every tuple contains only atomic attributes means exactly one value for each attribute. As per the rule of first normal form, an attribute of a table cannot hold multiple values. It should hold only atomic values.
Example: suppose Company has created a employee table to store name, address and mobile number of employees.
Emp_id | Emp_name | Emp_address | Emp_mobile |
101 | Rachel | Mumbai | 9817312390 |
102 | John | Pune | 7812324252, 9890012244 |
103 | Kim | Chennai | 9878381212 |
104 | Mary | Bangalore | 9895000123, 7723455987 |
In the above table, two employees John, Mary has two mobile numbers. So, the attribute, emp_mobile is Multivalued attribute.
So, this table is not in 1NF as the rule says, “Each attribute of a table must have atomic values”. But in above table the the attribute, emp_mobile, is not atomic attribute as it contains multiple values. So, it violates the rule of 1 NF.
Following solution brings employee table in 1NF.
Emp_id | Emp_name | Emp_address | Emp_mobile |
101 | Rachel | Mumbai | 9817312390 |
102 | John | Pune | 7812324252 |
102 | John | Pune | 9890012244 |
103 | Kim | Chennai | 9878381212 |
104 | Mary | Bangalore | 9895000123 |
104 | Mary | Bangalore | 7723455987 |
- Second Normal Form (2NF)
A table is said to be in 2NF if both of the following conditions are satisfied:
● Table is in 1 NF.
● No non-prime attribute is dependent on the proper subset of any candidate key of table. It means non-prime attribute should fully functionally dependent on whole candidate key of a table. It should not depend on part of key.
An attribute that is not part of any candidate key is known as non-prime attribute.
Example: Suppose a school wants to store data of teachers and the subjects they teach. Since a teacher can teach more than one subjects, the table can have multiple rows for the same teacher.
Teacher_id | Subject | Teacher_age |
111 | DSF | 28 |
111 | DBMS | 28 |
222 | CNT | 35 |
333 | OOPL | 38 |
333 | FDS | 38 |
For above table:
Candidate Keys: {Teacher_Id, Subject}
Non prime attribute: Teacher_Age
The table is in 1 NF because each attribute has atomic values. However, it is not in 2NF because non-prime attribute Teacher_Age is dependent on Teacher_Id alone which is a proper subset of candidate key. This violates the rule for 2NF as the rule says “no non-prime attribute is dependent on the proper subset of any candidate key of the table”.
To bring above table in 2NF we can break it in two tables (Teacher_Detalis and
Teacher_Subject) like this:
Teacher_Details table:
Teacher_id | Teacher_age |
111 | 28 |
222 | 35 |
333 | 38 |
Teacher_Subject table:
Teacher_id | Subject |
111 | DSF |
111 | DBMS |
222 | CNT |
333 | OOPL |
333 | FDS |
Now these two tables are in 2NF.
- Third Normal Form (3NF)
A table design is said to be in 3NF if both the following conditions hold:
● Table must be in 2NF.
● Transitive functional dependency from the relation must be removed.
So it can be stated that, a table is in 3NF if it is in 2NF and for each functional dependency
P->Q at least one of the following conditions hold:
● P is a super key of table
● Q is a prime attribute of table
An attribute that is a part of one of the candidate keys is known as prime attribute.
Transitive functional dependency:
A functional dependency is said to be transitive if it is indirectly formed by two functional dependencies.
For example:
P->R is a transitive dependency if the following three functional dependencies hold true:
1) P->Q and
2) Q->R
Example: suppose a company wants to store information about employees. Then the table Employee_Details looks like this:
Emp_id | Emp_name | Manager_id | Mgr_Dept | Mgr_Name |
E1 | Hary | M1 | IT | William |
E2 | John | M1 | IT | William |
E3 | Nil | M2 | SALES | Stephen |
E4 | Mery | M3 | HR | Johnson |
E5 | Steve | M2 | SALSE | Stephen |
Super keys: {emp_id}, {emp_id, emp_name}, {emp_id, emp_name, Manager_id}
Candidate Key: {emp_id}
Non-prime attributes: All attributes except emp_id are non-prime as they are not subpart part of any candidate keys.
Here, Mgr_Dept, Mgr_Name dependent on Manager_id. And, Manager_id is dependent on emp_id that makes non-prime attributes (Mgr_Dept, Mgr_Name) transitively dependent on super key (emp_id). This violates the rule of 3NF.
To bring this table in 3NF we have to break into two tables to remove transitive dependency.
Employee_Details table:
Emp_id | Emp_name | Manager_id |
E1 | Hary | M1 |
E2 | John | M1 |
E3 | Nil | M2 |
E4 | Mery | M3 |
E5 | Steve | M2 |
Manager_Details table:
Manager_id | Mgr_Dept | Mgr_Name |
M1 | IT | William |
M2 | SALSE | Stephen |
M3 | HR | Johnson |
n advance version of 3NF. BCNF is stricter than 3NF. A table complies with BCNF if it is in 3NF and for every functional dependency X->Y, X should be the super key of the table.
Example: Suppose there is a company wherein employees work in more than one
Department. They store the data like this:
Emp_id | Emp_nationality | Emp_dept | Dept_type | Dept_no_of_emp |
101 | Indian | Planning | D01 | 100 |
101 | Indian | Accounting | D01 | 50 |
102 | Japanese | Technical support | D14 | 300 |
102 | Japanese | Sales | D14 | 100 |
Functional dependencies in the table above:
Emp_id ->emp_nationality
Emp_dept -> {dept_type, dept_no_of_emp}
Candidate key: {emp_id, emp_dept}
The table is not in BCNF as neither emp_id nor emp_dept alone are keys. To bring this table in BCNF we can break this table in three tables like:
Emp_nationality table:
Emp_id | Emp_nationality |
101 | Indian |
102 | Japanese |
Emp_dept table:
Emp_dept | Dept_type | Dept_no_of_emp |
Planning | D01 | 100 |
Accounting | D01 | 50 |
Technical support | D14 | 300 |
Sales | D14 | 100 |
Emp_dept_mapping table:
Emp_id | Emp_dept |
101 | Planning |
101 | Accounting |
102 | Technical support |
102 | Sales |
Functional dependencies:
Emp_id ->; emp_nationality
Emp_dept -> {dept_type, dept_no_of_emp}
Candidate keys:
For first table: emp_id
For second table: emp_dept
For third table: {emp_id, emp_dept}
This is now in BCNF as in both functional dependencies left side is a key.
- Fourth Normal Form (4NF)
A relation is in the 4NF if it is in BCNF and has no multi valued dependencies.
It means relation R is in 4NF if and only if whenever there exist subsets A and B of the
Attributes of R such that the Multi valued dependency AààB is satisfied then all attributes of R are also functionally dependent on A.
Multi-Valued Dependency
● The multi-valued dependency X -> Y holds in a relation R if whenever we have two tuples of R that agree (same) in all the attributes of X, then we can swap their Y components and get two new tuples that are also in R.
● Suppose a student can have more than one subject and more than one activity.
- Fifth Normal Form (5NF)
A table is in the 5NF if it is in 4NF and if for all Join dependency (JD) of (R1, R2, R3, ..., Rm) in R, every Ri is a super key for R. It means:
● A table is in the 5NF if it is in 4NF and if it cannot have a lossless decomposition in to any number of smaller tables (relations).
● It is also known as Project-join normal form (PJ/NF)
Example
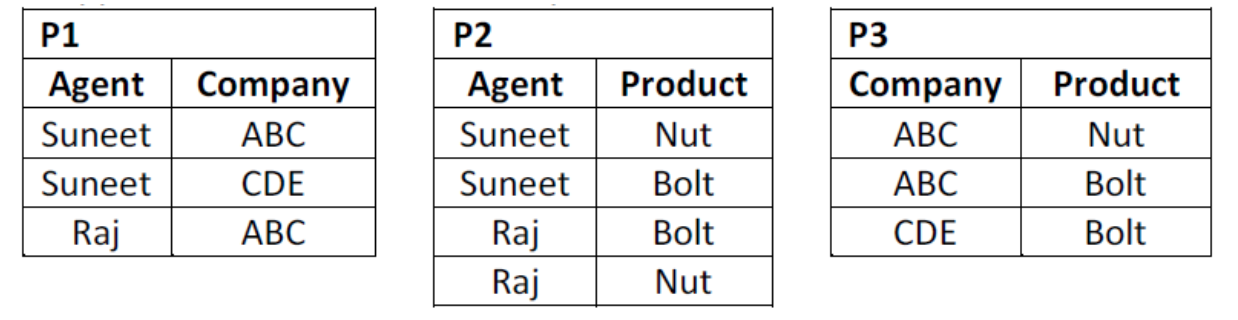
i. AGENT_COMPANY_PRODUCT (Agent, Company, Product)
Ii. This table lists agents, the companies they work for and the products they sell for those companies. ‘The agents do not necessarily sell all the products supplied by the companies they do business with.
An example of this table might be:
AGENT_COMPANY_PRODUCT | ||
Agent | Company | Product |
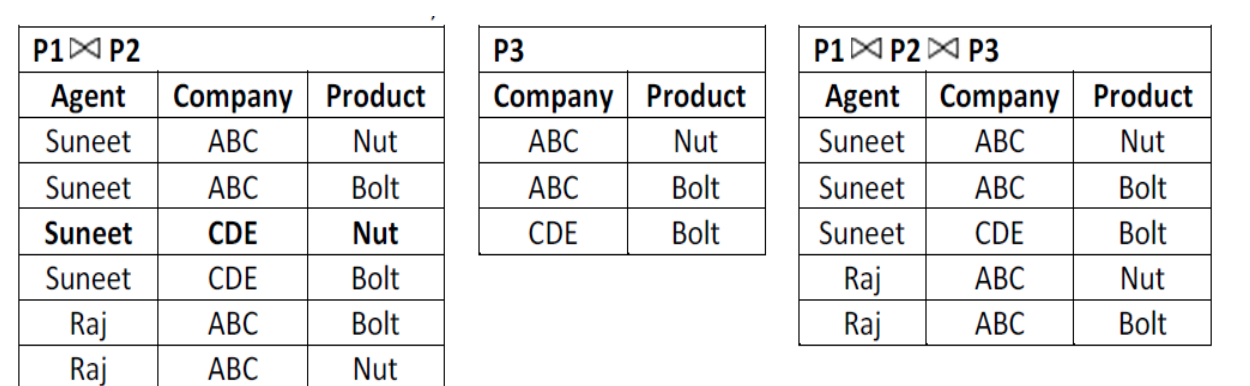
Suneet | ABC | Nut |
Raj | ABC | Bolt |
Raj | ABC | Nut |
Suneet | CDE | Bolt |
Suneet | ABC | Bolt |
1. The table is in 4NF because it contains no multi-valued dependency.
2. Suppose that the table is decomposed into its three relations, P1, P2 and P3.
i. But if we perform natural join between the above three relations then no spurious (extra) rows are added so this decomposition is called lossless decomposition.
Ii. So above three tables P1, P2 and P3 are in 5 NF
Q. 3) What is the join strategy ?
Ans : Join strategy
There are numerous joining techniques between two tables to perform. The distribution of data and columns chosen for joins greatly affects the implementation plan and the join strategy selected.
Broadly, there are four types of methods for joining:
● Nested Join
● Product Join
● Merge Join
● Hash Join
Nested join :
This join strategy uses 'special indexes' (be it a single primary index or a unique secondary index) from one of the join tables to retrieve a single record. The join condition should also fit a column from a single retrieved row to the second table's main /Secondary index. On the other table, a single row matches one or more rows .
Product join :
Product join compares every row in the second table from one table to every row, assuming the join condition as 1=1, and applies the filter to the result set if 'WHERE' determines some condition.
Example: If there are 20 rows in the 1st table and 10 records in the 2nd table, product join results in 200 (20X10) rows. In general, product interactions are triggered by errors
Popular triggers that can activate 'Product Join'
● The question defines neither the join condition nor the correct 'Where' clause.
● The condition of inequality is used as the joining condition
For product joining, there are 2 sub-strategies
- Big table Small table strategy:
When one table is very small, this technique comes into play. In this method, the small table will be duplicated into spools on all the AMPs. By scanning all-rows, the bigger table is then joined to the product spool.
2. General strategy:
All the rows from both tables are scanned and moved to different spools in this technique. Using a product joint, these spools will then be joined.
Merge Join:
For equi joins and exclusions as well, this is the most common join technique that comes into play.
For merge join, there are 5 sub-strategies
- PI-PI join : This method comes into play as the columns of both table columns are the key index of the respective tables. On local amps, rows will be directly joined (merge join) without transferring them to spool for joining.
2. PI- No PI Join : When joining columns of one table is the primary index, and joining columns of the second table is not the primary index, this technique comes into play.
On the relation columns, rows from the second table will be hashed and sorted by rowhash. To link with the 1st table, Rowhash is then sent to spool on the corresponding Amps. By scanning all-rows, the 1st table is then merged into a spool.
3. No PI - No PI join : When joining columns from both tables are not primary index columns, this technique comes into play. On the joining columns, rows from both tables are checked and hashed. For each table, Rowhash is then sorted and shifted to separate spools. Using a merge join, certain spools will be joined with each other.
4. Exclusion Join : When one table is used to remove data from another table, this technique comes into play. If 'NOT EXISTS' and 'NOT IN' are used, Exclusion Join is applicable.
5. Big table Small table strategy : When one table is very small, this technique comes into play. In this method, the small table will be duplicated into spools on all the AMPs. By scanning all-rows, the bigger table is then combined together into a spool.
Hash join :
This join approach is to join the merge family, but it performs much better than joining Merge Join & Product. When one table needs to be small enough to fit entirely in the memory, Hash join will be used.
There are 2 sub strategies for hash join
- Dynamic hash join : One table must be small enough to fit entirely into a single partition in the memory, and compared to another table, it should be very small. Dynamic hash join, without transferring large table to spool, offers the ability to join tables. Only when two tables are joined based on non-primary index columns will this work.
2. Classic / Partitioned hash join : When one table is too large for hash processing to fit into a single partition memory, the device splits the table into many smaller partitions that are small enough to fit into the memory available.
On both joining tables, hash join partitions are generated by hashing both table rows on their joining columns in such a way that rows from the hash join partition of one table can only fit rows in the hash join partition of the other table.
Q. 4) Define the term quer equivalence ?
Ans : Query equivalence
If both expressions generate the same set of records, all two relational expressions are said to be equal. We may use them interchangeably when two terms are identical. We can use any expression that provides better results, i.e.;
The equivalence rule states that expressions of two forms are the same or identical because in any legal database case, both expressions generate the same outputs. This implies that the expression of the first form may be replaced by that of the second form, and the expression of the second form may be replaced by the expression of the first form.
The query-evaluation plan optimizer therefore uses such an equivalence rule or process to turn expressions into logically equivalent ones.
For the transformation of relational expressions, the optimizer uses different equivalence principles for relational-algebra expressions. We will use the following symbols to define any rule:
θ, θ1, θ2 … : Used for the predicates being denoted.
L1, L2, L3 … : Used when denoting an attribute list.
E, E1, E2 …. : Represents the expressions of relational-algebra
Equivalence Rules
Rule 1: Cascade of σ
This rule notes the deconstruction into a series of individual selections of the conjunctive selection operations. Such a transition is referred to as a σ cascade.
σθ1 ᴧ θ 2 (E) = σθ1 (σθ2 (E))
Rule 2: Commutative Rule
Theta Join (θ) is commutative.
E1 ⋈ θ E 2 = E 2 ⋈ θ E 1
Rule 3: Cascade of ∏
This rule states that in the sequence of the projection operations, we only need the final operations, and other operations are omitted. A transformation of this kind is referred to as a cascade of ∏.
∏L1 (∏L2 (. . . (∏Ln (E)) . . . )) = ∏L1 (E)
Rule 4: The choices can be paired with Cartesian products and theta joins.
1. σθ (E1 x E2) = E1θ ⋈ E2
2. σθ1 (E1 ⋈ θ2 E2) = E1 ⋈ θ1ᴧθ2 E2
Rule 5: Associative Rule
This rule notes that associative operations are natural joining operations.
(E1 ⋈ E2) ⋈ E3 = E1 ⋈ (E2 ⋈ E3)
Rule 6: The union and intersection set operations are associative.
(E1 υ E2) υ E3 = E1 υ (E2 υ E3)
(E1 ꓵ E2) ꓵ E3 = E1 ꓵ (E2 ꓵ E3)
Q. 5) What is the lossless design ?
Ans : Lossless design
❏ If the data is not lost from the decomposing relationship, then the decomposition is lossless.
❏ The lossless decomposition ensures that the union of relationships can lead to the decomposition of the same relationship.
❏ If natural joins of all the decomposition give the original relation, the relationship is said to be lossless decomposition.
Now let's see an instance:
<EmpInfo>
Emp_ID | Emp_Name | Emp_Age | Emp_Location | Dept_ID | Dept_Name |
E101 | Jerry | 29 | Newyork | Dpt1 | Operations |
E102 | Henry | 32 | Newyork | Dpt2 | HR |
E103 | Tom | 22 | Texas | Dpt3 | Finance |
Decompose the table listed above into two tables:
<EmpDetails>
Emp_ID | Emp_Name | Emp_Age | Emp_Location |
E101 | Jerry | 29 | Newyork |
E102 | Henry | 32 | Newyork |
E103 | Tom | 22 | Texas |
<DeptDetails>
Dept_ID | Emp_ID | Dept_Name |
Dpt1 | E101 | Operations |
Dpt2 | E102 | HR |
Dpt3 | E103 | Finance |
Now, Natural Join is added to the two tables above,
The outcome will be −
EmpDetails ⋈ DeptDetails
Emp_ID | Emp_Name | Emp_Age | Emp_Location | Dept_ID | Dept_Name |
E101 | Jerry | 29 | Newyork | Dpt1 | Operations |
E102 | Henry | 32 | Newyork | Dpt2 | HR |
E103 | Tom | 22 | Texas | Dpt3 | Finance |
Therefore, the above relationship had decomposition without loss, i.e. no data loss.
Q. 6) What do you mean by Dependency preservation ?
Ans : Dependency preservation
❏ It is an integral restriction of the database.
❏ In the preservation of dependency, each dependency must satisfy at least one decomposed table.
❏ If the R-relationship is broken down into the R-relationship R1 and R2, then the R-relationship must either be part of R1 or R2, or it must be derived from the combination of the R1 and R2 functional dependencies.
❏ Suppose, for example, that there is a relation between R (A, B, C, D) and the set of functional dependencies (A->BC). Relational R is broken down into R1(ABC) and R2(AD), which maintains dependence since FD A->BC is part of the R1 relationship (ABC).
Decomposition D = { R1, R2, R3,,..,, Rm} of R is said to maintain dependence with respect to F if the union of F's projections on each Ri is equal to F. In D. R-join of R1, R1 over X, in other words. The dependencies are retained since each dependency in F represents a database constraint. If decomposition is not dependency-preserving, the decomposition loses any dependency.
Example :
Let R(A,B,C,D) be a relationship and set the FDs to F={ A -> B, A -> C, C -> D}.
Relationship R is broken down into —
R1 = (A, B, C) with FDs F1 = {A -> B, A -> C}, and
R2 = (C, D) with FDs F2 = {C -> D}.
F' = F1 ∪ F2 = {A -> B, A -> C, C -> D}
so, F' = F.
And so, F'+ = F+.
Thus, the decomposition is dependency preserving .
Q. 7) Define the term SQL3 ?
Ans : SQL3
Basically, SQL3 contains Object-Oriented dbms, OO-dbms data description and management techniques, while retaining the platform of relational dbms. DBMSs that support SQL3 are called Object-Relational or or-dbms 'based on this merger of concepts and techniques.
With these extensions, the latest version of SQL in development is also referred to as "SQL3". SQL3 object facilities mainly include extensions to SQL type facilities, but extensions to SQL table facilities may also be considered important. Additional facilities provide control structures for building, maintaining, and querying persistent object-like data structures to render SQL a computer-complete language.
The added equipment is intended to be compliant with the existing SQL92 specification upwards. This and other parts of the SQL3 Features Matrix focus mainly on the SQL3 extensions applicable to the modelling of artefacts.
In SQL, however, several other changes have also been made [Mat96]. Furthermore, it should be noted that SQL3 continues to be developed, so the definition of SQL3 in this Features Matrix does not necessarily reflect the final language requirements that have been accepted.
The parts of SQL3 that provide the primary basis for object-oriented structures to be supported are:
● Types that are user-defined (ADTs, named row types, and distinct types)
● For row types and reference types, type constructors
● For collection types, category constructors (sets, lists, and multi sets)
● Functions and procedures that are user-defined
● Assistance for big items (BLOBs and CLOBs)
Used of SQL
For interacting with a database, SQL is used. It is the basic language for relational database management systems, according to ANSI (American National Standards Institute). SQL statements are used for performing tasks, such as modifying database data or extracting database data.
Q. 8) Write short notes on MYSQL ?
Ans : MYSQL
MySQL is a relational database management system that runs on many platforms and is open-source. To support several storage engines, it provides multi-user access and is backed by Oracle.
MySQL is a fast and easy-to-use RDBMS that is used for the production of various small and large-scale applications. Various applications such as Joomla, WordPress, Drupal and many more are commonly used.
Under the terms of the GNU General Public License, as well as under a range of proprietary agreements, the source code of MySQL OpenSources is accessible. Several paid versions are available for proprietary use that provide additional functionalities. MySQL was originally developed by MySQL AB, which is now owned by Oracle Corporation, a Swedish company.
MySQL Server Software Version is available in various versions, such as Commercial Edition and Community Editions, etc., which are listed below:
- MySQL Community Edition
- MySQL Commercial Edition
- MySQL Enterprise Edition
- MySQL Standard Edition
- MySQL Classic Edition
- MySQL Cluster CGE
Features of MYSQL open sources :
- Platform Independent
- Replication
- Relational Database System
- Client/Server Architecture
- Query Language
- Easy to Use
Q. 9) What is DDl and write their commands ?
Ans : DDL
In reality, the DDL or Data Description Language consists of SQL commands that can be used to define the schema for the database. It basically deals with database schema definitions and is used to construct and change the configuration of database objects in the database.
Some of the commands that fall under DDL are as follows:
● CREATE
● ALTER
● DROP
● TRUNCATE
CREATE
It is used in the database for the development of a new table
Syntax
CREATE TABLE TABLE_NAME (COLUMN_NAME DATATYPES[,....]);
Example
CREATE TABLE STUDENT(Name VARCHAR2(20), Address VARCHAR2(100), DOB DATE);
ALTER
It is used to modify the database structure. This move may be either to change the characteristics of an existing attribute or to add a new attribute, likely.
Syntax
In order to add a new column to the table:
ALTER TABLE table_name ADD column_name COLUMN-definition;
To change the current table column:
ALTER TABLE MODIFY(COLUMN DEFINITION....);
Example
ALTER TABLE STU_DETAILS ADD(ADDRESS VARCHAR2(20));
ALTER TABLE STU_DETAILS MODIFY (NAME VARCHAR2(20));
Drop
It is used to delete both the structure of the table and the record.
Syntax
DROP TABLE ;
Example
DROP TABLE STUDENT;
TRUNCATE
It is used to erase from the table all rows and free up the space containing the table.
Syntax
TRUNCATE TABLE table_name;
Example
TRUNCATE TABLE STUDENT;
Q. 10) What is the DML and write their commands ?
Ans : DML
To change the database, DML commands are used. It is responsible for all forms of database changes.
The DML command is not auto-committed, which means all the changes in the database will not be permanently saved. There may be rollbacks.
Commands under DML
- SELECT
The Select Statement retrieves data from the database as defined by the constraints.
Select command with some clauses :
SELECT <COLUMN NAME>
FROM <TABLE NAME>
WHERE <CONDITION>
GROUP BY <COLUMN LIST>
HAVING <CRITERIA FOR FUNCTION RESULTS>
ORDER BY <COLUMN LIST>
Syntax
SELECT * FROM <table_name>;
Example
SELECT * FROM student;
OR
SELECT * FROM student
Where age >=15 ;
b. INSERT
The INSERT statement is a query from SQL. It is used for the insertion of data into a table row.
Syntax
INSERT INTO TABLE_NAME
(col1, col2, col3,.... Col N)
VALUES (value1, value2, value3, .... ValueN);
Or
INSERT INTO TABLE_NAME
VALUES (value1, value2, value3, .... ValueN);
c. UPDATE
This command is used to update or alter the value of a table column.
Syntax
UPDATE table_name SET [column_name1= value1,...column_nameN = valueN] [WHERE CONDITION]
d. DELETE
It is used to extract a table from one or more rows.
Syntax
DELETE FROM table_name [WHERE condition];